Pré requis:
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant |
DOSSIER : LES ROTATIONS d’une figure
|
|
·
Définition |
|
|
|
·
Rotation d’angle 60° |
|
|
|
·
Rotation particulière
(angle de 180°) |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
COURS
Définition
|
Soient un point
fixe O appelé centre de rotation,
et un angle de rotation
« alpha » : a donné en grandeur et sens
. Soit un point « M » quelconque ; traçons l’arc de
cercle de centre O , de rayon OM , tel que l’angle
MOM’ = a :
le point M’ sera dit le transformé de M dans la rotation de centre O ,
d’angle a. |
|
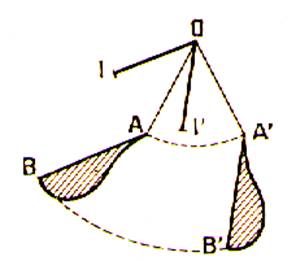
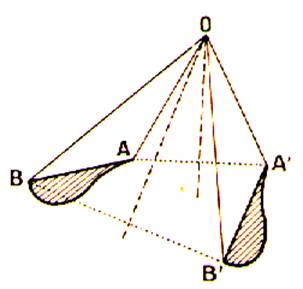
Soit la figure « F » ; on peut supposer que le
point O en fait partie ( au besoin , on peut l’y
relier par des segments auxiliaires OA , OB ). Faisons glisser F de manière que le point O reste fixe , le
segment OA tournant de l’angle AOA’ = a ;
la figure F toute entière subit une rotation. La rotation est donc un glissement d’une figure F , dans lequel : 1°)un certain point
O de cette figure est fixe . 2°)toute droite orientée
AB vient prendre une position A’B’ telle que l’angle ( AB , A’B’) soit égal à
a. Cela est évident pour une droite OI passant par O ; c’est
encore vrai pour une autre droite AB , parce qu’elle
tourne du même angle que sa parallèle OI |
|
|
Réciproquement : |
|
|
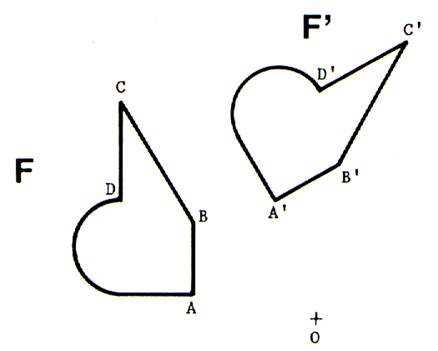
Si deux figures F et F’ sont superposables par glissement , la coïncidence pourra toujours se
réaliser : Exceptionnellement ,
par une translation ; en général , par une rotation. Soient en effet deux figures F et F’
superposables par glissement dont deux vecteurs homologues AB et A’B’ ne sont
passé équipollents ; nous allons prouver qu’elles ont un point double , c’est à dire un point O qui , dans les deux
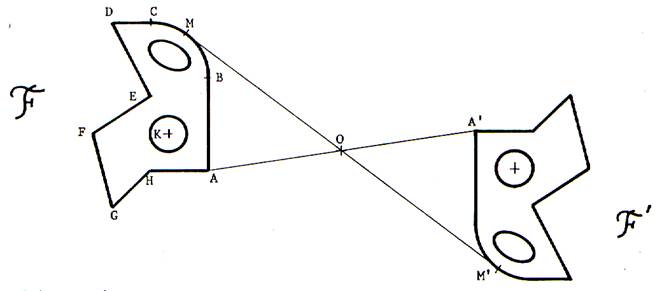
figures , occupe une position homologue. Trois méthodes pour le rechercher : 1°)Ce point O doit être
équidistant de deux points homologues A et A’ , donc sera sur la médiatrice
de AA’ ; il sera aussi sur la médiatrice de BB’. |
|
|
2°)Ce point O doit être
à égale distance de deux droites homologues AB et A’B’, donc sur une des
bissectrices des angles formés par ces droites ( une bissectrice parfaitement
déterminée , car les distances sont naturellement affectées de signes qui se
correspondent dans les deux figures) ; il sera aussi sur une bissectrice
de AC , A’C’. |
|
|
3°) Nous pouvons d’avance mesurer en grandeur et
signe l’angle a
de la rotation : c’est l’angle de deux vecteurs homologues AB et
A’B’ ; du point O on doit voir AA’ sous cet angle a , donc O sera sur l’arc ,
de corde AA’ , capable de cet angle ; et aussi sur un arc analogue de
corde BB’ . Quand on aura obtenu ce point O
, les triangles OAB et OA’B’ seront égaux ( la première méthode prouve
qu’ils ont les trois côtés égaux ) et de même sens ; cela prouve que O
occupe dans l’une et l’autre figure une position homologue ; donc une
rotation de centre O , d’angle a
, amènera F sur F’ . |
|
Rotation
d’angle 60°
|
|
|
F’
est l’image de F dans la rotation de centre O et d’angle 60° |
|
|
|
|
|
Cette rotation est appelée : symétrie centrale de
centre O |
|
|
|
|