Pré requis:

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent :

Transformations géométrique généralités

Objectif suivant

1°)La translation

2°)La symétrie centrale

3°)la symétrie orthogonale.(axiale)

4°)La rotation.

5°) permutation

6°) les coordonnées

Liste des cours de géométrie plane…

APPLICATIONS: voir la composition de transformation.

DOSSIER : TRANSFORMATIONS GEOMETRIQUES :

1°) Définition

2°) Les 4 transformations abordées au collège .

3°Les propriétés communes

4°) Liste des transformations principales

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

COURS

1°) Définition :

Une « transformation » , c’est le remplacement de tout point donné M par un autre point M’ , d’après une loi fixée : de telle sorte que la position du point M’ soit fonction de la position du point M.

Etant donnée une figure F , si à tous les points de cette figure on applique cette loi , on obtient une autre figure F’ qui est dite la transformée de la figure F : ce mot général « transformée » devant être complété ( ou remplacé ) par un autre mot qui indiquera avec plus de précision de quelle transformation il s’agit.

B) Les 4 transformations abordées au collège sont :

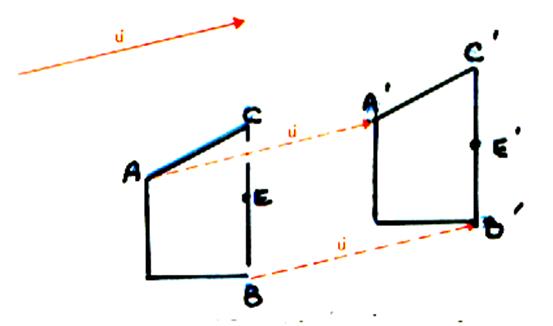
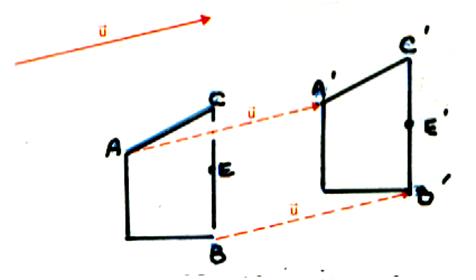
1°) La translation d’un vecteur

Pour plus d’info : SOS cours : Translation ; translation « vecteur » ; SOS Cours : Vecteur .

Translation du vecteur

Dans la translation on dit que :

A’ est l’image de A

Cela signifie que :

trantra

2°) la symétrie centrale

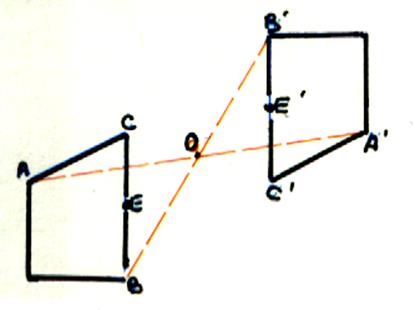
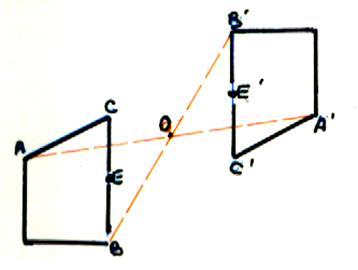
SOS COURS : symétrie centrale

Dans la symétrie de centre O

le point A’ est l’image de A ;

Ce qui signifie que le point « O » est le milieu du segment AA’

tranCe

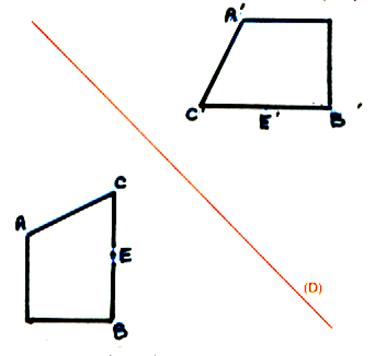
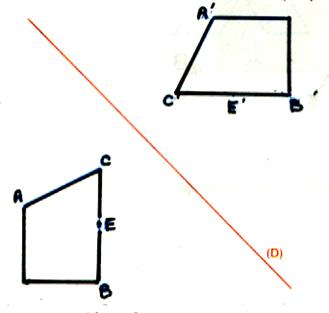
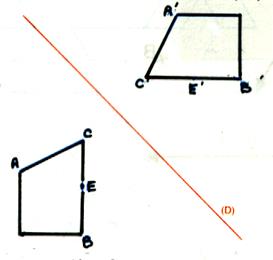
3°) La symétrie orthogonale.

SOS Cours :Symétrie orthogonale

SOS Cours :Axe de symétrie

La symétrie orthogonale d’axe (D) est aussi appelée « symétrie axiale » ou « la réflexion d’axe (D) ».

a) Si le point A n’est pas sur la droite (D) :

A’ est l’image de A ; ce qui signifie que la droite (D) est la médiatrice du segment AA’ .

b) Si le point A est sur la droite (D) , A’ est confondu avec A.

tranOrt

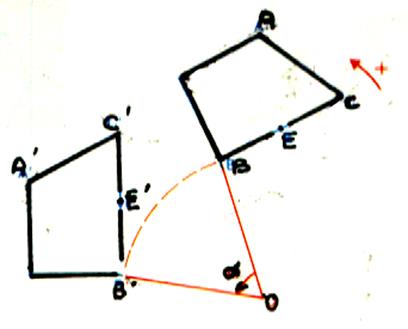
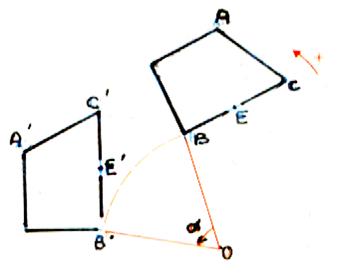
d) La rotation

SOS Cours : La rotation.

La rotation de centre « O » et d’angle « alpha ».

Le point A’ est l’image de A ;cela signifie que

Le rayon OA = OA’ et

Remarque : Quand on tourne dans le sens inverse des aiguilles d’une montre , on dit que l’on tourne dans le sens trigonométrique ; (indiqué par la flèche)

tranRo

3°Les propriétés communes :

Ces quatre transformations ont en commun :

Si A , B , C ont pour image A’ , B’ , C’ par l’une ou l’autre de ces transformations
De conserver les longueurs	AB = A’B’
De conserver les angles	=
De conserver l’alignement	Si A , B , C sont alignés , alors A’ , B’ , C’ le sont aussi .
De conserver les aires	Les triangles ABC et A’B’C’ ont la même aire.
Remarque : Ces quatre transformations conservent les éléments remarquables des triangles.

4°) Liste des transformations principales :

1° ) Les divers « déplacements » :
Translation
Rotation
2°) les oppositions ou symétries, qui, en géométrie plane, sont des cas particuliers de déplacements.
-Symétrie centrale
-Symétrie orthogonale
3°) les divers modes de projections
- Projection par rapport à une direction quelconque.
-Projection orthogonale
4 °) l’homothétie
5° ) la similitude

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°)Qu’est ce qu’une « transformation :

2°)Citer les quatre principales transformations :

3°)Quelles sont les propriétés communes à ces transformations ?

4°)Citer les principales transformations

5°) IDENTIFIER les transformations ( les nommer )

a)

b)

c)

d)

e)