Pré requis:

Les coordonnées d’un point dans un repère cartésien

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : Les coordonnées d’un point dans un repère cartésien Axes de coordonnées ( vecteurs)

Objectif suivant : Le point "coordonnées" 2°) Le point d'intersection de deux droites perpendiculaire.. 3°) étude d'un système de deux équations de deux droites.

tableau 1°) Repérage : 2°) Vecteur : présentation des objectifs.

	DOSSIER : Vecteur : CALCULS des COORDONNEES D’UN POINT
	( Point obtenu par translation ou par symétrie.)
	I) La TRANSLATION DE VECTEUR donné
	a ) par la représentation graphique.
	b) détermination de la position du point « B » par le calcul
	II) SYMETRIE d’un point PAR RAPPORT A UN POINT
	Recherche des coordonnées du point B symétrique de A par rapport au point « I »
	III) SYMETRIE d’un point PAR RAPPORT A L’ORIGINE DU REPERE
	IV ) SYMETRIE d’un point PAR RAPPORT A UN AXE.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

COURS :

I) TRANSLATION DE VECTEUR donné ,

	SOS Cours : vecteur dans un plan,
Un vecteur étant donné par ses coordonnées dans une base , , tout point a pour image dans la translation le point de coordonnées Pour  ; et pour Avec D’ où les coordonnées du vecteur Et les coordonnées du vecteur « v »
Exemples d’exercices  : Données : Les coordonnées du vecteur « v » sont :  ; et un point « A » tel que Questions : Quelles sont les coordonnées de l’image de A dans la translation a )par la représentation graphique. b) par le calcul.
Nous écrivons : ( lire : le point A à pour image le point B par la translation du vecteur « v ») ; telle que a )détermination de la position du point « B » par la représentation graphique. Procédure : On trace le vecteur «  » ; ensuite on place le point « A » et à partir du point « A » , on trace une parallèle au vecteur « v » dont la longueur est égale à la norme du vecteur ; (voir ; tracer d’un parallélogramme) On relève les valeurs des coordonnées du point « B » sur le repère : et On écrit alors : on peut simplifier l’écriture : b)détermination de la position du point « B » par le calcul : ( Voir le calcul des coordonnées du vecteur ) Les données  sont : et  ; avec « A » à pour image dans la translation de le point « B » de coordonnées On en déduit que : les coordonnées du vecteur sont :  ; Nota : au collège ; l’écriture les coordonnées du vecteur sont :  ; peut se simplifier ; sachant e : Et on accepte de ‘écrire que les coordonnées du vecteur AB sont :  ; Nous savons que ; puisque : on peut donc écrire = Alors  ; on calcule les coordonnées de = ; soit ; et Alors  ; on calcule les coordonnées de Soit : ( sos calculs) Conclusion : Les coordonnées du point « B » sont : On écrit :

	II) SYMETRIE PAR RAPPORT A UN POINT.
	Pré requis : a) Voir "opposé" d'un nombre et la symétrie par rapport à O. b) calcul des coordonnées d’un vecteur c) le vecteur colinéaire opposé. d) le vecteur nul .
Recherche des coordonnées du point « B » symétrique du point « A » par rapport au point « I » : Exemple : I ( 3 ; 2) ; A ( 2 ;1)
Un point « » d’abscisse et d’ordonnée étant donné : . Tout point a pour image dans la symétrie centrale , le point « B » tel que : Ou
Remarque : si je connais les coordonnées du vecteur IA , je peux soit en déduire, ou calculer les coordonnées du vecteur IB .
1°) Calcul des coordonnées du vecteur : sur « » = xA - x I = ( +2 ) – ( +3) = ( -1 ) ( SOS calcul numérique?) sur yi = y A - y I = ( + 1) – ( + 2) = ( -1) conclusion : les coordonnées du vecteur = ( -1 ; -1 ) ; et les coordonnées du vecteur « opposé » est – = ( + 1 ;+ 1 ) « l’opposé du vecteur ? ? ? »

2°) Coordonnées du vecteur

sur « x_i » : x_B x _I = ( x_B ) – ( +3)

sur « y_i »    : y _B y _I = ( y_B) – ( + 2)

soit ( x_B 3 ; y_B 2)

le vecteur ( x_B3 ; y_B –2 ) = le vecteur si et seulement si :

x_B3  = 1 et si y_B 2 = 1 :

après calculs : x_B  = 4 et y_B = 3 ;

les coordonnées de B sont ( 4 ;3 )

Conclusion : les coordonnées du point B symétrique du point A par rapport au point I sont ( + 4 ; + 3 )

(commentaire : les coordonnées du point B sont aussi les coordonnées du vecteur telles que vecteur ( + 4  ; + 3 )

III) SYMETRIE PAR RAPPORT A L’ ORIGINE DU REPERE

A ( xA ; y A) a pour image B (- xA ;- y A) dans la symétrie . Pour obtenir la symétrie d’un point par rapport à l’origine il suffit de prendre les valeurs « opposées » aux coordonnées données . Exemple : Soit un point A( +3 ; +2)  ; donner les coordonnées du point B par rapport au point O , origine d’un repère . Si A ( +3 ; +2) ; son image ( B) dans la symétrie centrale et B ( opp.+3 ; opp.+2) Soit B ( -3 ; - 2)

IV ) SYMETRIE PAR RAPPORT A UN AXE.
La symétrie peut se faire par rapport à l’axe des abscisses ou des ordonnées.	( voir symétrie axiale ; orthogonale ; réflexion)
Exemples : a) A ( + 3 ; +2 ) a pour image dans la symétrie par rapport à ( O ) le point A’ ( + 3 ; -2 ) (* -2 est l’opposé de +2) b) A ( + 3 ; + 2 ) a pour image dans la symétrie par rapport à ( O ) le point A’’ ( - 3 ; + 2 ). (* - 3 est l’opposé de +3)
Conclusion : 1°) Dans la symétrie par rapport à l’axe des abscisses , un point A ( x A ; y A) a pour image le point A’ ( x A ; opp. y A) ; ou A’( x A ; - y A)  2°) Dans la symétrie par rapport à l’axe des ordonnées , un point A ( x A ; y A) a pour image le point A’’ (opp. xA ; y A) ; ou A’ ( - x A ; + y A)

TRAVAUX AUTO FORMATIFS

CONTROLE

A) Traduire : A ( x_A ; y _A) a pour image B (- x_A ;- y _A) dans la symétrie .

B) voir cas par cas :

I) TRANSLATION DE VECTEUR donné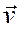

	SOS Cours : vecteur dans un plan,
Si nous écrivons : T : A B ( lire : le point A à pour image le point B par la translation du vecteur « v ») ; telle que a ) Faites une représentation graphique : b) Déterminer la position du point B par le calcul :

II) SYMETRIE PAR RAPPORT A UN POINT

Comment opère –t –on pour rechercher les coordonnées du point B symétrique de A par rapport au point « I » ? :

III) SYMETRIE PAR RAPPORT A L’ ORIGINE DU REPERE.

A ( x_A ; y _A) a pour image B (- x_A ;- y _A) dans la symétrie .

Comment peut- on obtenir les coordonnées du point dans la symétrie d’origine O , dans un repère ?.

IV ) SYMETRIE PAR RAPPORT A UN AXE.

Soit un point A ( x_A ; y _A) quelles sont les coordonnées de A ‘ et A’’ symétriques axiales dans un repère cartésien ?.

EVALUATION

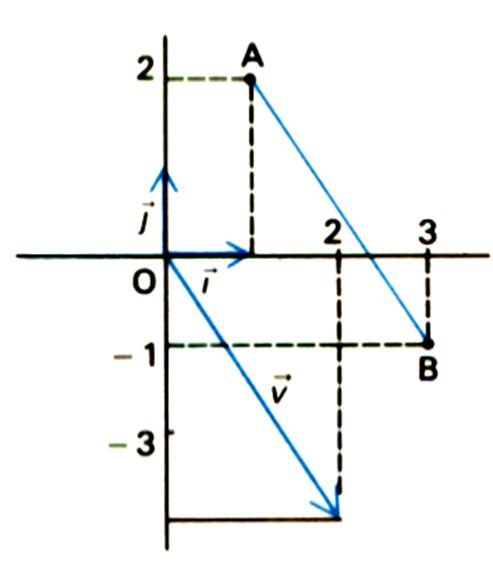
1°)Les coordonnées du vecteur « v » sont :

( 2 ,-3) ; et un point « A » tel que A (1 ;2)

Questions : quelles sont les coordonnées de l’image de A ; notée « B » dans la translation T

a )par la représentation graphique.

b) par le calcul.

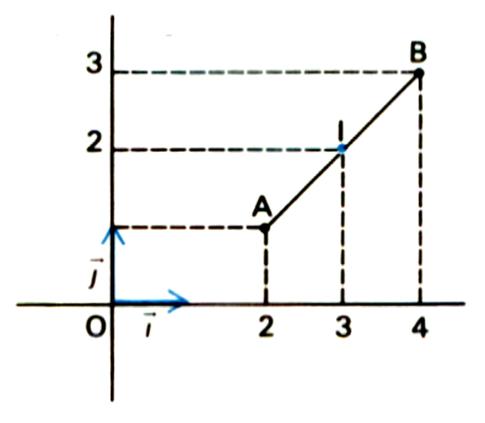
2°) Rechercher les coordonnées du point B symétrique de A par rapport au point « I » : On donne I ( 3 ; 2) ; A ( 2 ;1).

a) solution graphique .

b) par le calcul .

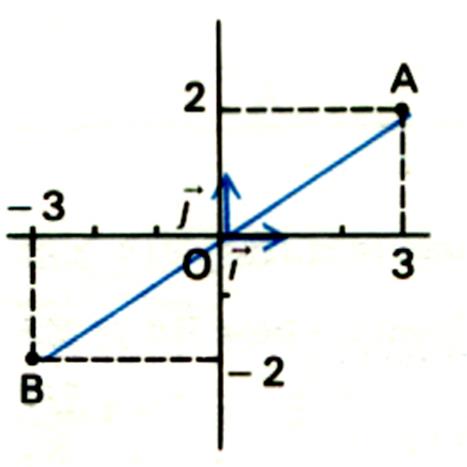
3°) Soit un point A( +3 ; +2)  ; donner les coordonnées du point B par rapport au point O , origine d’un repère .

a) Solution graphique

b) Par le calcul

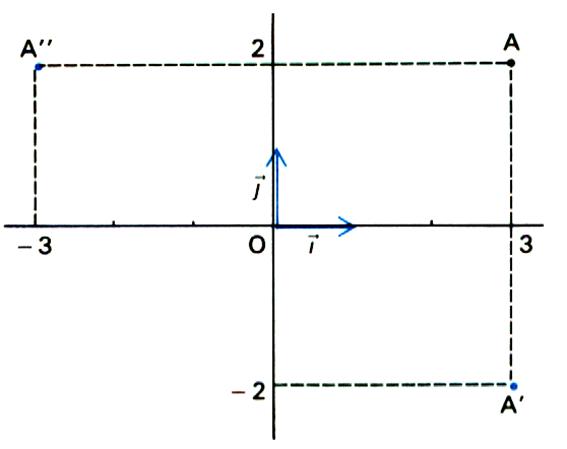
4°) Soit un repère cartésien orthogonal et un point A ( +3 ; +2) :

par rapport à l’axe ( O ) et par rapport à l’axe ( O )

a) Par le calcul.

b) Par le graphique