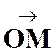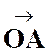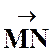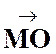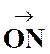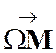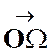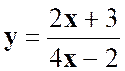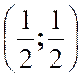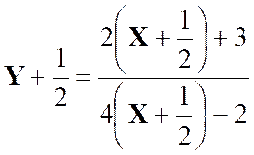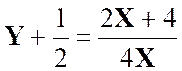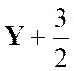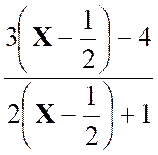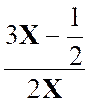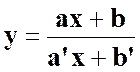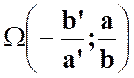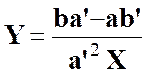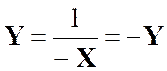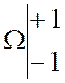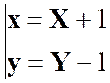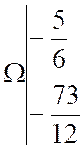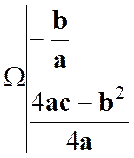·      Présentation d’un repère non ortho -non normé.

                                                     :      Pb.1 et pb 2

·      Cours (  suite 1 ) : distance entre deux points.

Changements d’axes par translation : pb. 3 ; 4 ; 5 ; 6

·      Cours (suite 2) :  pb. 7 ; 8 ; 9

·      Cours (suite 3) :cas « y= ax² + bx + c »  et  Généralisation….

Deux droites indéfinies «  x ‘ O x » ; «  y ‘ O y » se coupent au point « O ». Si l’on marque sur  «  x ‘ O x » un vecteur  unitaire  et sur  «  y ‘ O y » un vecteur unitaire , les droites deviennent des axes orientés. Les longueurs de   et  ne sont  par forcément égales ( repère non ortho-non normé)

Soit « M » un point du plan.

Le vecteur  se décompose suivant « Ox » et « Oy » en deux vecteurs  et  :

             =   +  

et nous avons déjà vu  ( cours : addition de  (après pb 18….)  que :

 =    x             

   =   y   

donc :            =  x     +   y                   ( relation 1 )

Les nombres algébriques « x » et « y » , uniques pour « M », sont les coordonnées cartésiennes du point « M ». Dire que  « x » et « y » , sont les coordonnées de « M » ou que :     =  x     +   y               revient exactement au même.

« x » s’appelle « abscisse »   et « y » s’ appelle « ordonnée »

Problème 1

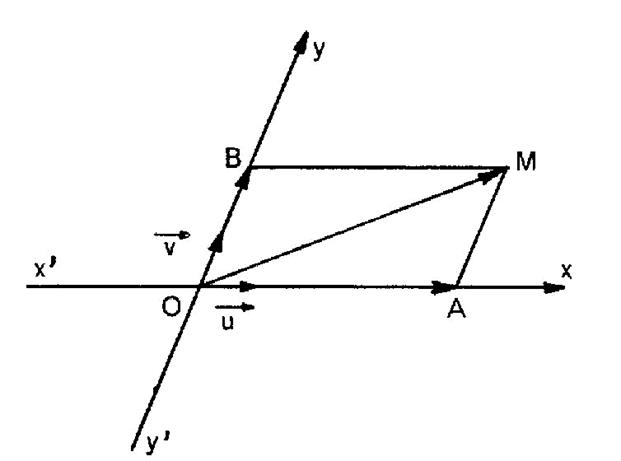
Soit deux points « M » de coordonnées  ( x₀ ; y₀ )   et « N » de coordonnées ( x₁  ; y ₁ ).

Quelles sont les mesures scalaires des projections du vecteur  sur les axes ?

La projection sur « Ox » est faite  parallèlement  à « Oy »    et sur «  Oy » parallèlement à « Ox ».

( faire une figure )

Info + °sur les mesures algébriques des composantes…. ;…

Solution :

On écrira : le vecteur    =    +    ( relation 2 )

Ou : « X » et « Y » étant   les mesures scalaires des projection de        on écrit :      X    +   Y      =    +    ( relation 3 )

Mais d’après l’énoncé :

 = x₀ +   y₀                              ou : = -  x₀ -   y₀

                                                                                                                         ( relation (4)

   =  x₁   +  y ₁ .

En portant les  résultats (4) dans la relation ( 3 ) nous pouvons écrire :

X    +   Y      =   =     ( x₁ -  x₀ )     +   (y ₁ - y₀ ) .

D’où

X =   ( x₁ -  x₀ )  ( abscisse de l’extrémité (moins) abscisse de l’origine.)

Y =  ( y ₁ - y₀ )     ( ordonnée  de l’extrémité (moins) ordonnée  de l’origine.)

Problème 2

Les points « M » et « N » ont pour coordonnées respectives ( - 3 ; + 2 )  et ( 5 ; - 4) . Quelle sont les mesures des projections de  sur les axes ? 

( Faire la solution graphique.)

Réponses :

X = 5  - ( - 3)   ; X = 8

Y = - 4 – 2   ;    Y = - 6  

Cours (  suite 1 )

Dans la pratique , les axes « x’ O x »  et «  y ’O y » sont perpendiculaires et les vecteurs unitaires  et   ont même longueur. On dit alors que les axes sont « orthonormé » ( voir :orthonormal)  ou  que  et constituent une base orthonormée.

Les résultats acquis au problème « 1 » subsistent et les projections de        sont

x₁ -  x₀

y ₁ - y₀

Mais ici on peut déduire la distance de deux points « M » et « N » donnée  par la formule :

 =  ( x₁ -  x₀ )²  +  ( y ₁ - y₀ )²

Cette formule  de la distance de deux points en axes rectangulaires est fort utile à connaître , notamment pour une étude analytique du cercle ou de la sphère ( avec un terme ( en « z ») de plus)

Pré requis : « Pythagore »

( Faire la solution graphique.)

Changements d’axes par translation :

Voir : Soit un point « M » positionné relativement à des vecteurs unitaires :  et      a pour coordonnées «  x ; y » . On prend une nouvelle origine   dont les coordonnées par rapport aux anciens axes sont  «   et   » . les nouveaux axes  sont parallèles aux anciens. Relativement aux nouveaux axes « M » acquiert les nouvelles coordonnées «  X ; Y » .Trouver les relations entre : «  x ; y » «  X ; Y » «   et   »

Solution : Les axes parallèles ont même vecteur unitaire . Dés lors les données de l’énoncé sont :

 = x + y            ( 1 )

 =  X  + Y          ( 2 )

 =  +           ( 3 )

Et comme on sait que :  =    +                         ( 4 )

En remplaçant il vient :

 x + y        =   +     +  X  + Y                      ( 5 )

Et par conséquent :

 x = X  +

 y   =  Y  +

Ce sont les formules du changement d’axes par translation. :

A savoir :

les coordonnées anciennes = Les coordonnées nouvelles + (plus) Les coordonnées de la nouvelle origine.

Problème 4 :

Que devient la relation   ( 1 )   lorsque l’on transporte les axes parallèlement à eux –mêmes , au point    de coordonnées :

Solution :

Les formules du changement d’ axe sont :

x    = X +

y    = Y +                                                l’ensemble  ( 2 )

Portons ces évaluations dans ( 1 )

    ou     ce qui s’écrit encore : 

la réponse est donc :           ( 3 )

Problème 5

Que devient la relation :   lorsque l’on transporte les axes parallèlement à eux –mêmes , au point    de coordonnées

Orientation de la solution :

=  =        

Réponse :

Problème 6

Que devient la relation :  quand on transporte les axes parallèlement  à eux-mêmes au point : ?

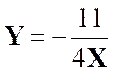
Réponse :

Cours (suite 2) :

Noter  que les nouvelles formes acquises  après changement d’axes mettent en évidence par le point   est centre de symétrie de la représentation graphique des relations envisagées.. par exemple au problème « 4 » nous avons trouvé :    . Si on change « X » en « -X » on obtient    

Les changement de « X » en « -X »   entraîne celui de « Y » en « -Y » : Le point     est centre de symétrie.

Problème 7

Que devient la relation :    lorsque l’on transporte les axes parallèlement à eux-mêmes au point :     ?.

Solution : les formules du changement d’axes sont :

Portons dans la relation ( 1) :

                         Y – 1  = 2 ( X + 1 ) ² – 4 ( X + 1 )  + 1

Développons :

                         Y – 1  = 2  X ² + 4 X + 2 – 4 X – 4  + 1

Et réduisons    Y = 2 X ²

Problème 8

Que devient  la relation :  «  y = 3 x²  + 5 x – 4 »                              (1 )

Lorsque l’on transporte les axes parallèlement  à eux – mêmes  au point :   

Indications pour arriver à la solution :

 Formules :  « x = X -  »      ;  «  y = Y -  »

Porter dans ( 1) développer et réduire :

Réponse :                   Y = 3 X ²

Problème 9

Que devient l’expression : «  y = a x² + b x + c »

Quand on transporte les axes parallèlement à eux-mêmes au point

Réponse :   «  Y = a X ² »

Cours (suite 3) :

Noter que le changement d’axes met en évidence que la droite   est axe de symétrie de la représentation graphique de « y = a x² + b x + c ».

 On a trouvé en effet au problème « 9 » : : «  Y = a x ² » , si on change « X »  en « -X » on obtient :

                              «  Y ₁  = a ( - X ) ²  =   a X ²  = Y

A deux valeurs opposées de « X » correspond  la même valeur de « Y ». Il y a symétrie par rapport au nouvel axe des « Y ».

TRAVAUX AUTO FORMATIFS.

CONTROLE

EVALUATION.

Refaire les problèmes…du cours  …… ;;;;