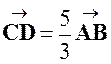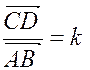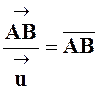Pré requis

Multiplier un vecteur par un scalaire « k » c’est construire un autre vecteur Dont le support est parallèle à celui de , ou confondu avec celui de , dont le sens est celui de si « k » est positif, contraire à celui de si « k » est négatif, et dont la norme « » est telle que CD = .

Et La longueur CD = AB ou

On écrit aussi : = k .

Exemple :

Le vecteur vaut les 5/3 du vecteur soit

170

On écrit aussi : = k .

Et cette relation indique à la fois :

· Que les supports de et sont parallèles.

· Que : CD = AB

· Que le signe de « k » précise le sens relatif de et

En particulier , une relation du type : = k . ; implique que les trois points sont alignés

En résumé :

Soient un vecteur et un nombre réel « k » , il existe alors un vecteur défini par = k

Remarques particulières :

1 . =

0. =

k . =

Activités :

Tracer le bipoint (A,B) représentant de ; le bipoint ( B,C) ) représentant de puis le bipoint (C,D) représentant de . On constate que le bipoint ( A,D) représentant de :

+ + que l ’ on peut noter = 3

Que peut - on dire des supports de et ?...................................................

Le produit d’un vecteur par un réel « k » est le vecteur de même support que et tel que = k . ( attention au cas ou « k »0)

Le produit du vecteur nul par un nombre réel « k » est le vecteur nul .

Remarques :

si « k » = 0 alors = puisque 0 =

si « k »  0 et ont le même sens , si « k »  0 ils sont de sens contraires.

2°) Propriétés :

Pour tous vecteurs et et pour tous réels k et k’

· k. + k’. = ( k + k’ ) .

· k . + k . = k . ( + )

· k . ( k’ . ) = ( k . k’)

Applications numériques :

Utilisation de la formule k. + k’. = ( k + k’ ) .

1°) Résoudre dans l’ensemble des vecteurs l’équation :

- 5 = 2 - 3

on répond : - 2 = 5 - 3

- = 2 ; = - 2

2°)Trouver le réel « a » tel que ¹

a² - 2 a + =

On répond : (a² - 2 a + 1) =

Comme ¹ alors a² - 2 a + 1 = 0

Puisque a² - 2 a + 1 = ( a – 1 )² = 0 ; a = 1

La suite va aider à préparer le cours sur l’addition géométrique de vecteurs : ( voir la somme des forces en statique graphique)

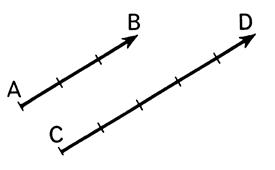
Etant donné deux vecteurs et dont les supports sont parallèles ou confondus ( condition sine qua non) ,on définit leur rapport comme étant le nombre algébrique « k » par lequel il faut multiplier pour retrouver .

On peut écrire : le rapport du vecteur CD sur le vecteur AB est égal à « k ».

Soit :

Et cela signifie que : = k . qui est une autre forme d’écriture.

Toute la question est l’obtention de la valeur absolue de « k » (noté : ).

Elle est très simple lorsqu’il existe une fraction de l’unité de longueur choisie qui est contenue un nombre entier de fois dans la longueur « AB » et un nombre entier de fois dans la longueur « CD ».

Ce n’est pas le cas le plus habituel et nous admettons que par encadrements successifs, nous arrivons à une valeur « k » satisfaisante.

En particulier, si sur l’axe orienté qui porte le vecteur on a marqué le vecteur unitaire , qui a pour longueur « un » et qui est dirigé dans le sens positif de l’axe , le rapport entre le vecteur et le vecteur est précisément ce que l’on appelle « la mesure algébrique du vecteur « AB » et que l’on note en prenant bien garde de ne pas surligner « AB » :