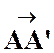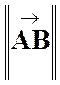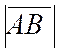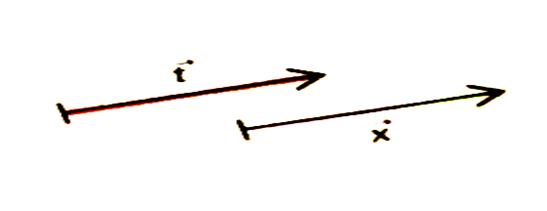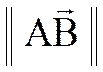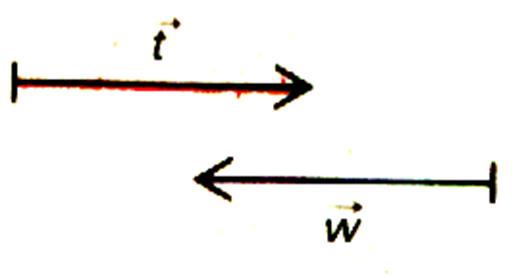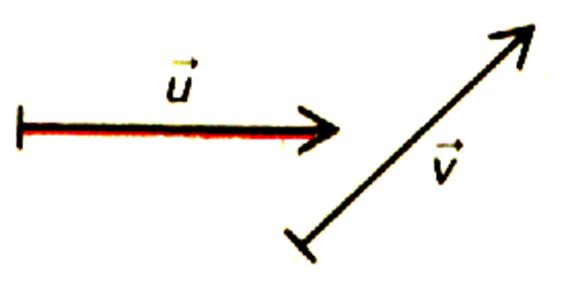ACTIVITE :
Consignes : Dans
le plan « P » tracer : -
Le bipoint (C,D) équipollent à (A,B) -
Le bipoint (E,F) équipollent à (A,B). -
Combien peut - on tracer de bipoints équipollents
à (A,B) dans le plan « P » ?
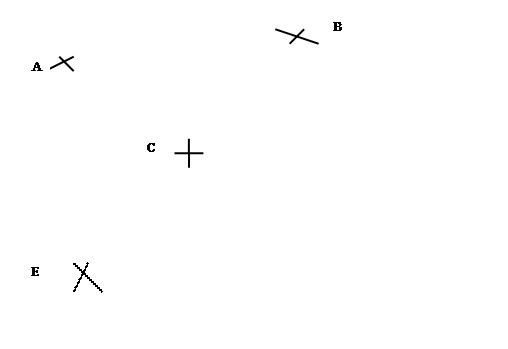
Réponse :
Une infinité
|
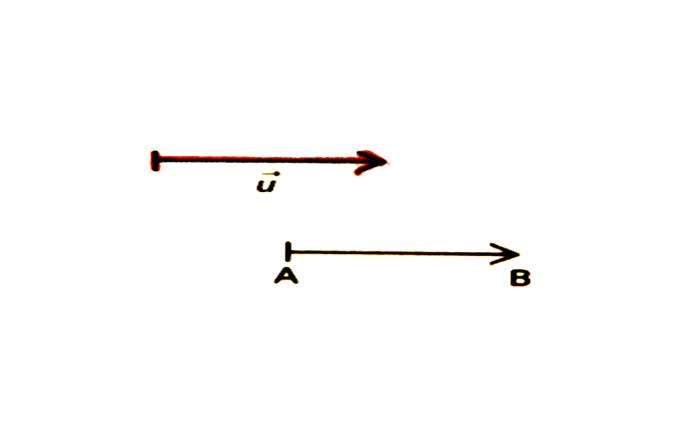
Définition : On appelle
« VECTEUR » l’ensemble des bipoints, du plan , équipollents à
un bipoint donné. |
|
Remarques : Un vecteur se représente par l’un de ses
bipoints. Et on le
note On le
note également : On peut aussi désigner un vecteur par une lettre
minuscule empruntée à la fin de l' alphabet.: |
|
Sur une figure géométrique ou sur
un schéma , on dessine une flèche pour
représenter un vecteur.

|
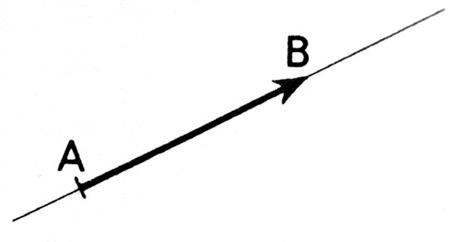
Par définition : on peut
dire aussi que : · Un vecteur est un segment de droite orienté. · Le symbole Ce vecteur
est décrit par un point mobile
parcourant le segment AB dans le sens de A vers B . |
|
|
- Le point A est
l’origine du vecteur AB et le point B l’extrémité de ce vecteur . - La
droite AB est appelé « support » du bi point représentant ce
vecteur . - La
longueur AB est appelée
« norme » du vecteur AB. |
|
|
Un
vecteur est nul lorsque sa norme est
nulle . Si un point A et B sont confondus
, le Bipoint noté ( A ,B ) est
« nul » , il représente le vecteur « nul » noté : Il en est
de même pour tous les vecteurs du type
(
pour en savoir plus : coordonnées du vecteur
nul) |
|
|
se souvenir que : (voir : mesure algébrique d ' un bipoint )
1°) ON appelle "mesure" l'évaluation d'une
quantité en la comparant à une quantité déterminée.
2°) On appelle "longueur" la dimension d'un
objet linéaire de l'une à l'autre de ses extrémités.
(l'unité de longueur est le mètre)
3°) On appelle "distance" ,l'intervalle (ou les
intervalles )qui existe entre deux points ,ou deux objets. (L'intervalle est généralement noté
"u" associé à un segment de droite d'unité "UN ")
|
|
|
|
|
2° )
NORME d'un
vecteur :
|
|
|
Une unité de distance étant choisie , la distance
du point A au point B , ou du point B au point A est appelée « NORME » du vecteur
. On sait que le vecteur noté : On notera: |
|
|
lire :
« norme (ou module) du vecteur
« V » |
|
|
|
lire :
« norme du vecteur (noté : |
|
Se souvenir que |
|
|
d ( A,B) |
lire :
« distance du
bipoint A à B » |
|
mes. [AB] |
lire :
« mesure du segment AB » |
|
On peut écrire que |
|
|
II |
|
On
peut conclure que : d
( A,B) = 4
, donc II Traduit
en écriture littérale : la distance
entre les deux points Aet B est de 4 unités ou la
norme du vecteur AB est de 4
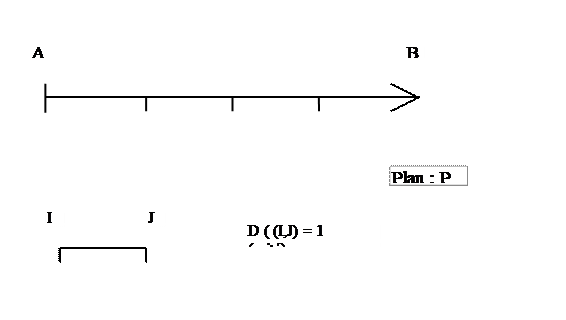
![]() II =
4
II =
4
|
|
NORME d’un vecteur : A
retenir : |
|
La NORME d’un vecteur (noté II Soit II |
|
|
Voir objectif repérage sur une
droite. La distance de 2 points étant un nombre « en valeur
absolue » ou nul , la norme d’un vecteur est donc un nombre « sans
signe » ou nul . · La norme du vecteur nul est égale à zéro . noté : II · Pour un vecteur donné , les bipoints équipollents qui le représentent
, ont des supports parallèles.
L’ensemble de ces supports forment une direction. (direction d’un vecteur) |
|
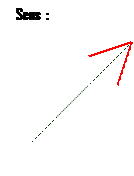
Sens 2
·
Sens 1

 SENS
SENS
 Pour une direction donnée , on peut définir 2 sens .
Pour une direction donnée , on peut définir 2 sens .
|
3°)CARACTERISTIQUES D ‘UN VECTEUR |
|
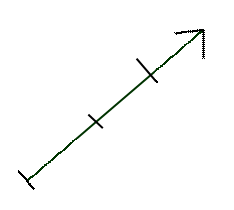
Dans un plan
(P) , un vecteur noté : n sa direction n son sens n sa norme |
Autre façon de l’écrire :
=
vecteur + +
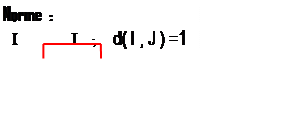

|
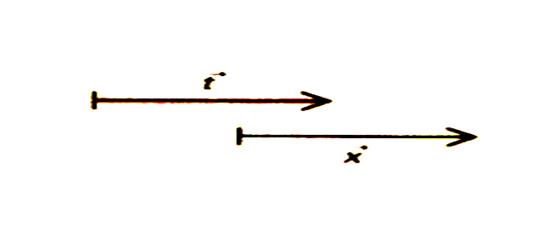
Quelques affirmations : · Si deux vecteurs sont représentés par le même bipoint , ils sont
égaux. ·
Si deux vecteurs ont la même norme ils ne sont
pas égaux (sauf cas : ils ont alors même direction et sens ). La norme d’un vecteur « nul » est
positive ou nulle. |
|
|
4°) EGALITE DE DEUX VECTEURS : A savoir : Deux vecteurs sont égaux s’ils ont -
même direction -
même sens , -
même longueur |
|
|
Cas 1 : ils sont parallèles ; ils ont le même
sens ; la même direction ; la même longueur : ils égaux |
Cas 2 : ils
sont parallèles ; ils ont le même sens ; la même direction ;
la même longueur : ils égaux |
|
|
ATTENTION ! ! ! ! ! !Les
vecteurs du cas 1 ne sont pas
égaux au cas 2 ; ils n’ont
pas la même direction. |
||
|
Comparaisons de vecteurs : |
|
|
|
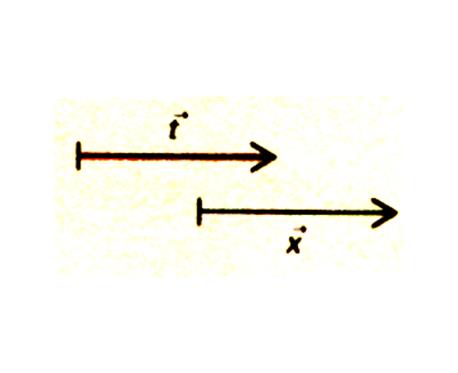
Les vecteurs sont égaux .
|
|
|
|
Les deux vecteurs n’ont pas le même sens |
|
|
|
Les deux vecteurs sont de longueur différentes :
|
|
|
|
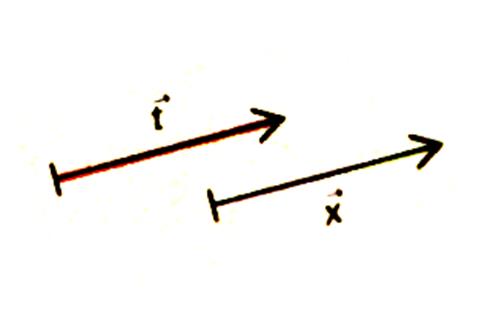
Les deux vecteurs n’ont pas la même direction .
|
|
|
|
Conditions d’égalités : Soit deux
vecteurs
Ces formules
peuvent être utiles pour montrer qu’un quadrilatère est un
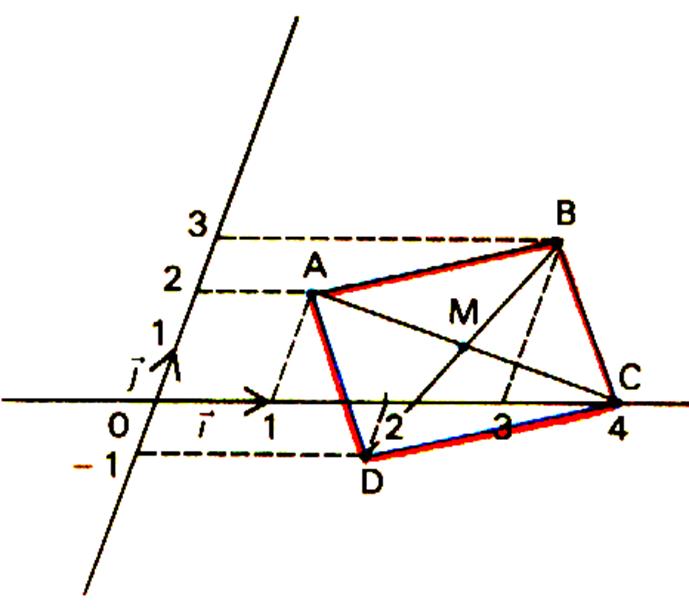
parallélogramme . Activité : Placer les points A ( 1 ; 2 ) ; B (
3 ; 3 ) ; C ( 4 ;0) ; D ( 2 ; - 1 ) dans un repère ( O ; |
||
|
|
||
|
1re méthode : SOS :
calculs
donc |
||
|
2e méthode : · « M » milieu de ( A , C ) ; M ( · « N » milieu de ( B , D ) ; N
(
Les diagonales se coupent en
leur milieu. C.Q.F.D. |
||
|
TRAVAUX AUTO FORMATIFS. |
||
|
VOCABULAIRE: (prendre le dictionnaire éventuellement) 1°)°)qu'est ce qu'une mesure? 2°) Qu'est ce qu'une longueur? 3°)Qu'est ce qu'une distance ? 4°) Dans un bipoint ,si les deux points sont
confondus ,il représente le vecteur .......... . Il est
noté : ............ 5°) Comment appelle-t-on la distance comprise
entre l'origine et l'extrémité du
bipoint ? 6°)Quelles sont les caractéristiques d'un vecteur
? 7°)Traduire 8°)Traduire en langage littéral : a) b) "Si |
||
|
EVALUATION : 1°) Comparer les groupes de deux vecteurs :
sont-ils égaux ? pourquoi ? |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2°) Placer les points A ( 1 ; 2 ) ; B (
3 ; 3 ) ; C ( 4 ;0) ; D ( 2 ; - 1 ) dans un repère ( O ; Suivant deux méthodes : « les vecteurs égaux » ou
« les milieux des diagonales » |
||
|
1re méthode : SOS : calculs
donc Conclusion : ( A , B , C , D ) ayant
deux côtés opposés parallèles et égaux est un parallélogramme. |
|
|
|
2e méthode : M milieu de
( A , C ) ; M ( N milieu
de ( B
, D ) ; N ( Les diagonales se coupent en leur milieu. C.Q.F.D. |
|
|
Soit un
vecteur donnez sa norme :