Pré
requis:
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : : |
Objectif
suivant : |
DOSSIER : LE VECTEUR et SON OPPOSE
2°)
Coordonnées d’un vecteur et de
son opposé
4°)Différence de deux vecteurs
|
|
Interdisciplinarité |
|
Corrigé évaluation |
Tout
vecteur à « son » opposé :
Rappel :
les caractéristiques du vecteur sont : direction ;sens ;
norme.
Un vecteur est
dit « opposé » à un autre
vecteur si il à la même direction ,la même norme
, mais il est de « sens contraire ».
(On peut dire : le vecteur bleu est l ’ opposé du vecteur noir ou le vecteur noir est l’opposé du vecteur bleu)
Rappel « vecteur nul » : un vecteur est nul
si l’extrémité et l’origine sont confondues :
![]()
![]()
![]()
ainsi AA =
II = O
2°)
Coordonnées d’un vecteur et de
son opposé :
Remarque : la somme de deux vecteurs
colinéaires égaux opposés est
égal au vecteur nul .
![]()
![]()
![]()
AI + I
A =
O
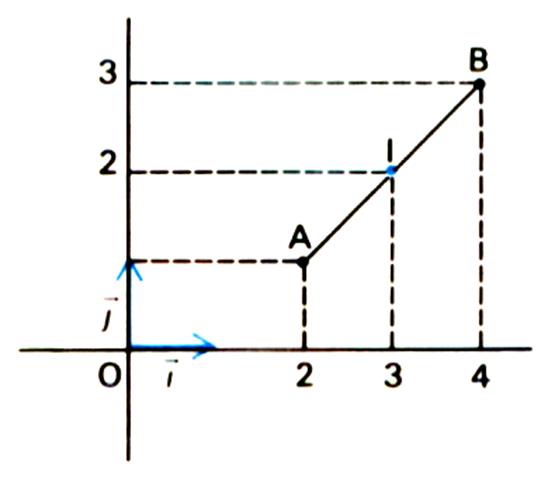
3° )
Calcul des coordonnées d’ un vecteur et de son opposé , connaissant les coordonnées des extrémités
du vecteur : ( les points
A et I sont les bipoints des vecteurs)
|
Recherche des coordonnées du
vecteur IA et AI : On donne les coordonnées des
points A et I : Exemple : I ( 3 ;
2) ; A ( 2 ;1) |
|
|
|
|
|
Soit un point « I »
d’abscisse xI et d’ordonnée yI étant donné : I (xI ;
yI ) . Et un point A ( xA ;
yA) |
|
|
1°) Calcul des coordonnées du
vecteur IA : ( extrémité moins origine ) sur « x sur « y |
|
2°)Calcul des coordonnées du vecteur AI :
( extrémité moins origine ) sur « x sur « y |
ANALYSE
DES résultats :
Les coordonnées du vecteur
IA sont ( -1 ![]() ;
-1
;
-1 ![]() )
)
Les coordonnées du vecteur
AI sont ( +1 ![]() ;+1
;+1
![]() )
)
conclusion :
![]() les vecteurs
IA et AI ; ou AI et IA
ont des coordonnées de valeurs opposées
les vecteurs
IA et AI ; ou AI et IA
ont des coordonnées de valeurs opposées
Leur somme est égale à « 0 »
Voir la relation
de Châles :
![]()
![]()
![]()
![]()
![]()
![]()
A I + IA =
AA ou IA + AI =
II
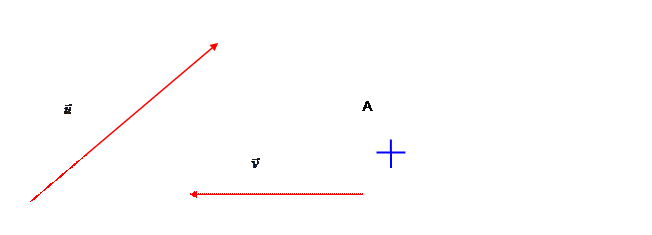
4°)Différence de deux vecteurs : exemple : ![]() et
et ![]()
![]()
![]() Représentation graphique de l’
opposé de
Représentation graphique de l’
opposé de ![]() :
:
Procédure :
Tracer le bipoint (A,B) représentant de
![]() puis
le bipoint (A,C) représentant de
puis
le bipoint (A,C) représentant de ![]() .
.
Donner un représentant du vecteur
![]() qu ‘il faut ajouter
à
qu ‘il faut ajouter
à ![]() pour obtenir
pour obtenir
![]() :
:
![]() =
=
![]() +
+ ![]() ;
; ![]() est représenté par le bipoint.
est représenté par le bipoint.
On appelle « différence des vecteurs ![]() et
et
![]() le vecteur
le vecteur ![]() qu ‘il faut ajouter
à
qu ‘il faut ajouter
à ![]() pour obtenir
pour obtenir ![]() .On
note
.On
note ![]() =
= ![]() -
-
![]() ;
;
Dans la représentation graphique de la différence de deux vecteurs on
trace la somme des vecteurs
![]() =
= ![]() + (-
+ (- ![]() ) on dit aussi
) on dit aussi ![]() =
= ![]() +
opp (
+
opp (![]() )
)
Pour
la compréhension voir l ‘ objectif DR2
(soustraction de deux nombres décimaux)
Tracer le bipoint (B,D) représentant du
vecteur ![]() ’ ,opposé du vecteur
’ ,opposé du vecteur ![]() , le bipoint (A , D)
, le bipoint (A , D)
représente la somme ![]() +
+
![]() ’ .
’ .
Que peut -
on dire des bipoints (A,D) et ( C,B) ?
La différence de deux vecteurs ![]() et
et ![]() est égale à la somme du vecteur
est égale à la somme du vecteur ![]() et
du vecteur
et
du vecteur ![]() ’
opposé du vecteur
’
opposé du vecteur ![]() .
.
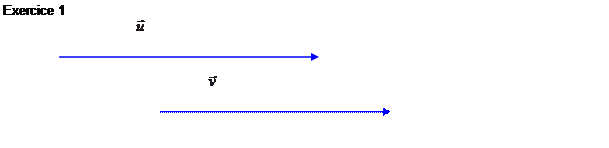
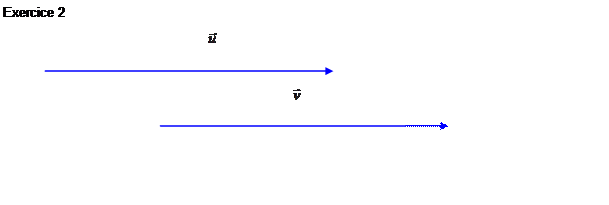
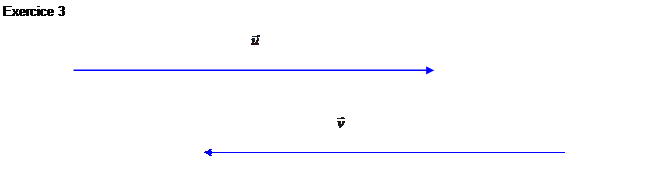
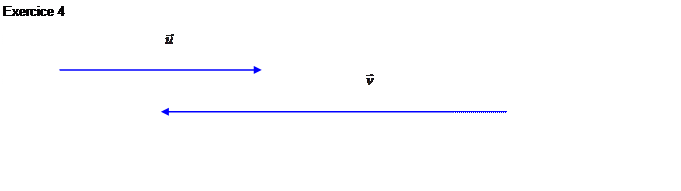
Exercices : Tracer un
représentant de la différence ![]() des vecteurs
des vecteurs ![]() et
et ![]() dan les cas suivants :
dan les cas suivants :