Pré
requis:
|
Repérage d’un point
sur un axe( abscisse d’un point) |
|
|
|
|
|
|
|
|
Les
nombres relatifs ( présentation) |
|
Environnement du dossier:
|
|
|
|
Classe de 6éme |
|
Objectif précédent : |
1°)Droite
et représentation graphique 2°)
calcul de coordonnées d’un point obtenu par
translation ou symétrie 3°) repérage
dans un repère cartésien ou non cartésien . |
Tableau 2°)
Liste des cours sur le repérage |
DOSSIER:
COORDONNEES D ' UN POINT dans un plan
divisé en 4 zones .( dans un
repère cartésien)
( avec des
valeurs de « x » et
« y » négatives positives ou nulles)
|
|
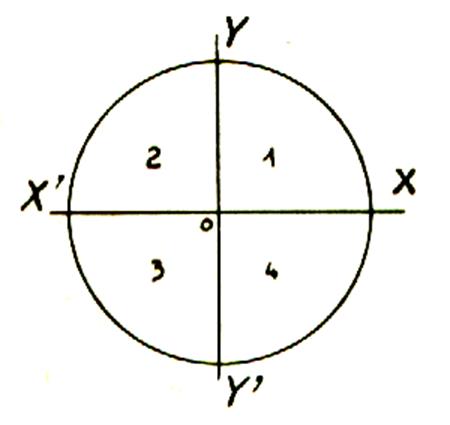
1°)
Repérage d ‘un point dans un « plan divisé en
quatre parties ou zones ou quadrants » |
|
|||||
|
|
2°)
Procédure permettant de trouver les coordonnées
d ’ un point dans un plan |
|
|||||
|
|
3°)
Division du cercle trigonométrique |
|
|||||
|
|
|
|
|||||
|
|
4°)
ACTIVITES |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
Repère cartésien orthonormé
( le plus utilisé en mathématique , le moins
utilisé en sciences) |
|
|
1°)
Repérage d ‘un point dans un « plan
divisé en quatre parties ou zones
ou quadrants »
Une fois deux axes tracés ; et O (origine) du repère :on
obtient 4 zones ( ou parties ou
quadrants).
|
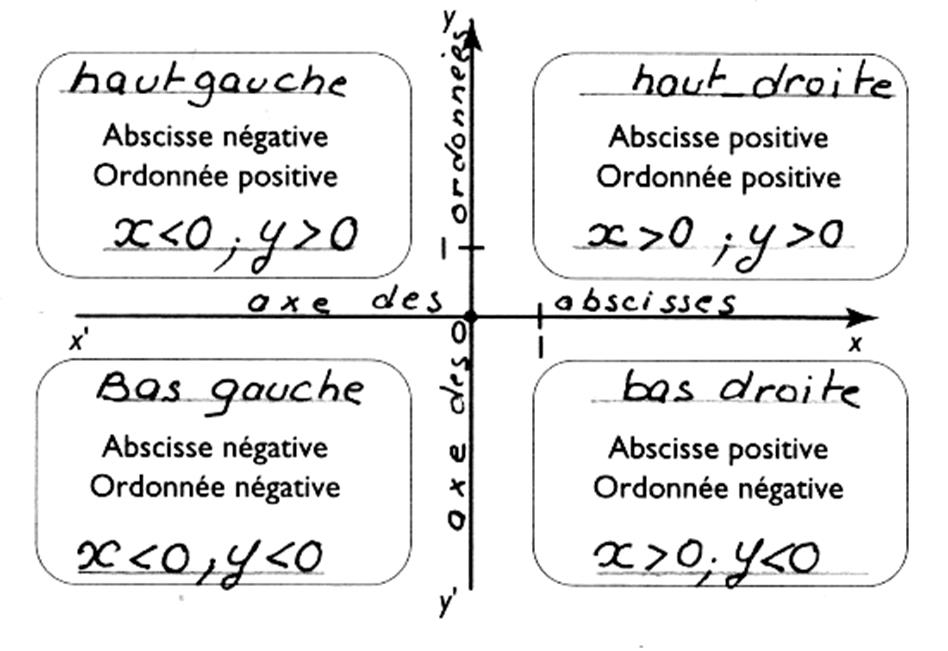
N° des zones |
situations |
Signe de l'abscisse |
Signe de l'ordonnée |
|
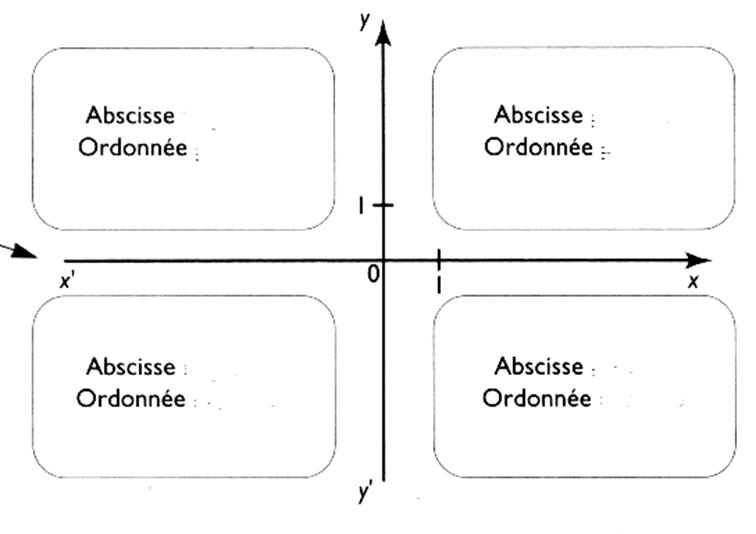
1er quadrant |
En Haut à droite |
Positif |
Positif |
|
2ème quadrant |
En Haut à gauche |
Négatif |
Positif |
|
3ème quadrant |
En Bas à gauche |
Négatif |
Négatif |
|
4ème quadrant |
En bas à droite |
Positif |
Négatif |
Représentation
:
|
|
2°)
Procédure permettant de trouver les coordonnées
d ’ un point dans un plan :
Pour trouver les coordonnées d’un point dans un plan :
A partir du point : On peut parler
de "projection d’un
point " Il faut tracer une
droite parallèle à l ’ axe des ordonnées (y’y) pour trouver la valeur de l ’ abscisse et une autre droite
parallèle à l ’ axe des abscisses (x’ x)
pour trouver la valeur de l
‘ordonnée.
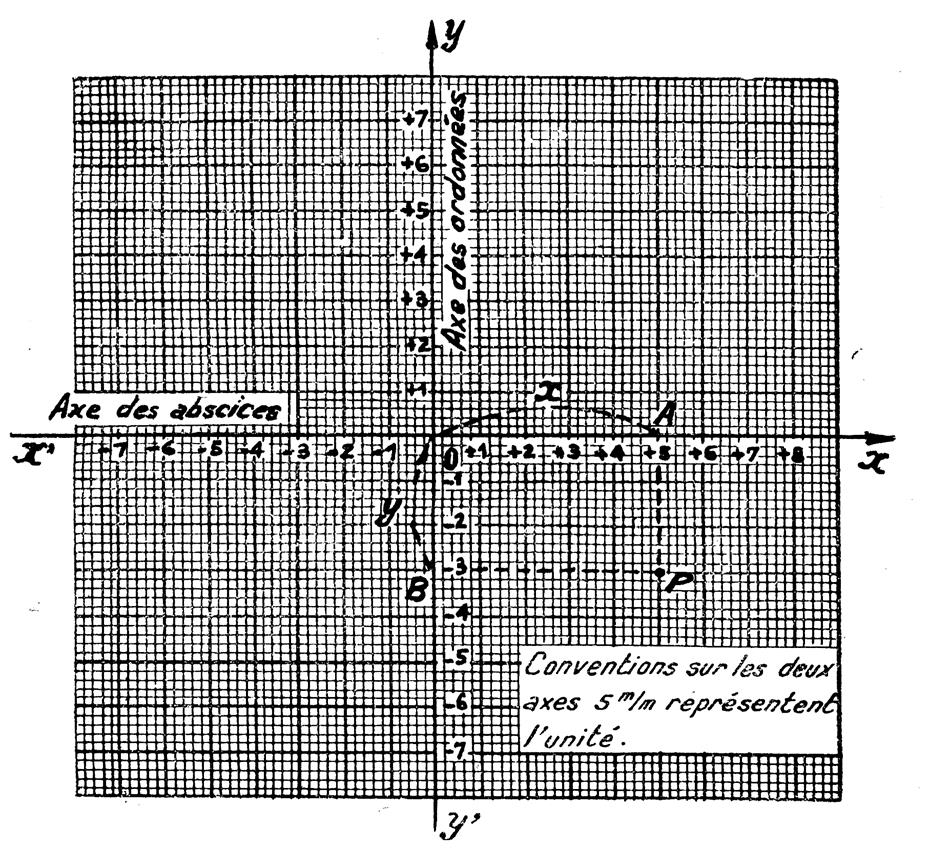
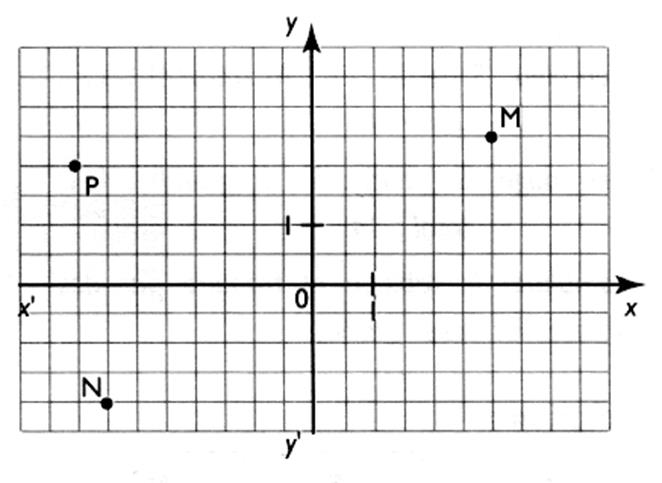
Exemple :
les projections du point « M » nous
permettent de lire sur les axes les
coordonnées de ce point
M : Mx = +3 et M y = +2,5
|
|
Les coordonnées d’un point
dans un repère du plan sont des nombres relatifs ; ils peuvent
être positifs. ou négatifs
|
|
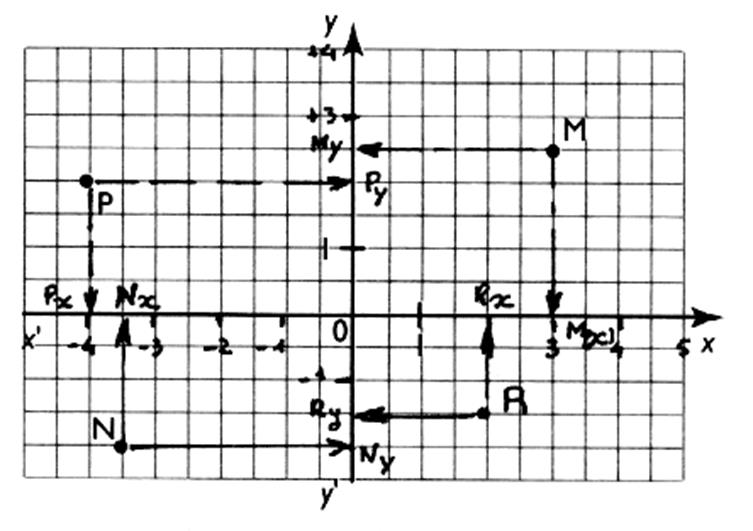
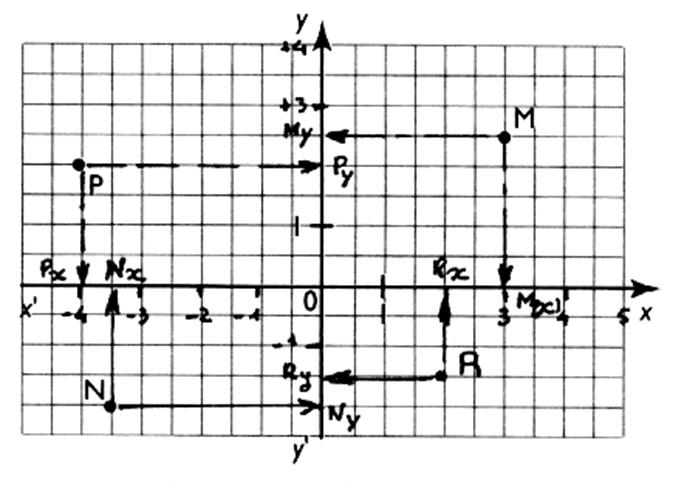
Coordonnées des points :
|
|
Abscisse |
Ordonnée |
Coordonnées |
Nota |
|
M |
Mx = + 3 |
M y = +2,5 |
M ( 3; 2,5) |
x>0 ; y
>0 |
|
P |
Px
= -4 |
P y = +2 |
P ( -4 ; +2 ) |
x <0 ; y
> 0 |
|
N |
Nx = -3,5 |
N y = -2 |
N ( -3,5 ; -2) |
x<0 ; y < 0 |
|
R |
Rx = +2 |
R y =
-1,5 |
R ( 2 ; -1,5) |
x>0 ; y
< 0 |
3°) Division du cercle trigonométrique :
Ces zones sont utilisées pour
travailler sur le cercle
trigonométrique :
Soit
un plan en 4 parties égales ; le
point « 0 » sera le centre du
cercle
Les quatre parties sont appelées : quadrant
|
Les axes 0x et Oy sont orientés positivement
vers la droite et vers le haut . , les angles
croissent de 0 à 2 p
, à partir de 0x et dans le sens des aiguilles d’une montre
. Le quadrant xOy est appelé « premier
quadrant ». Le quadrant x’Oy est appelé « deuxième
quadrant ». Le quadrant x’O
y’ est appelé « troisième
quadrant ». Le quadrant xOy’ est appelé
« quatrième quadrant ». |
|
|
Remarques : - Un point appartenant au premier quadrant a pour coordonnées: Des valeurs de x
>0 et y > 0 - Un point appartenant au deuxième
quadrant a pour
coordonnées: Des valeurs de x < 0 et y > 0 - Un point appartenant au troisième
quadrant a pour
coordonnées: Des valeurs de x < 0 et y < 0 - Un point appartenant au premier quadrant a pour coordonnées: Des valeurs de x >0 et y < 0 |
|
4°)
ACTIVITES
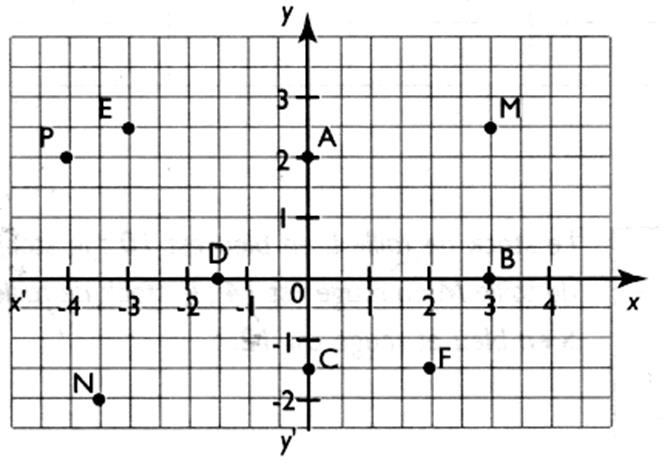
Activité 1 :
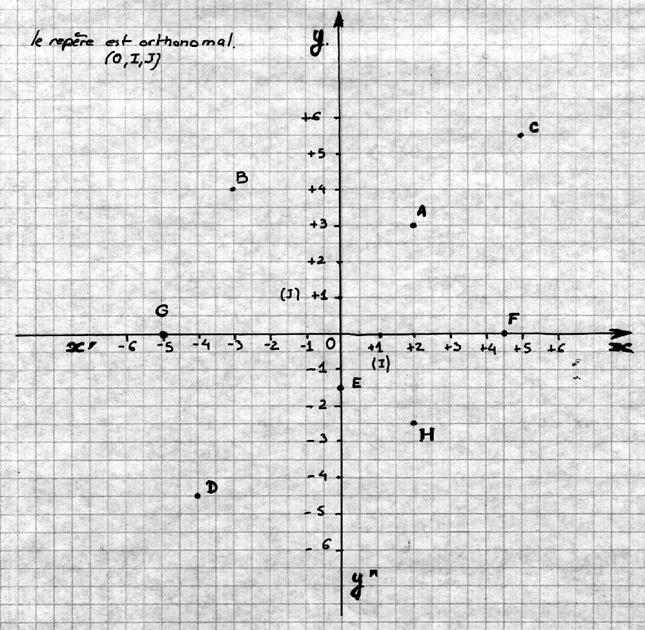
Dans le repère :
compléter les graduations et
Placer les points A ( 0;2) ; B ( 3 ; 0 )
; C ( 0 ; - 1,5 ) ; D ( - 1,5 ; 0
) ; E ( - 3 ; 2,5 ) et F ( 2 ; - 1,5)
|
Donner les coordonnées des points : N ( __;__)
P (__;__) M ( __;__) |
|
Solution activité 1:
|
N (-3,5 ; 2) P (-4 ; 2) M ( 3;
2,5) |
|
Applications :
|
|
|
|
|
|
|
|
|
Terminer la graduation et donner les coordonnées des points. |
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
Contrôle
HD : Haut Droite ; HG : Haut Gauche ; BG : Bas gauche ; BD : Bas Droite
|
|
Dites quels sont les signes des
valeurs des coordonnées d’un point se
trouvant :
|
dans la |
Signe
de x |
Signe
de y |
|
première zone ( H D) |
|
|
|
Deuxième zone ( H G ) |
|
|
|
Troisième zone ( B G ) |
|
|
|
Quatrième zone ( GD) |
|
|
EVALUATION
|
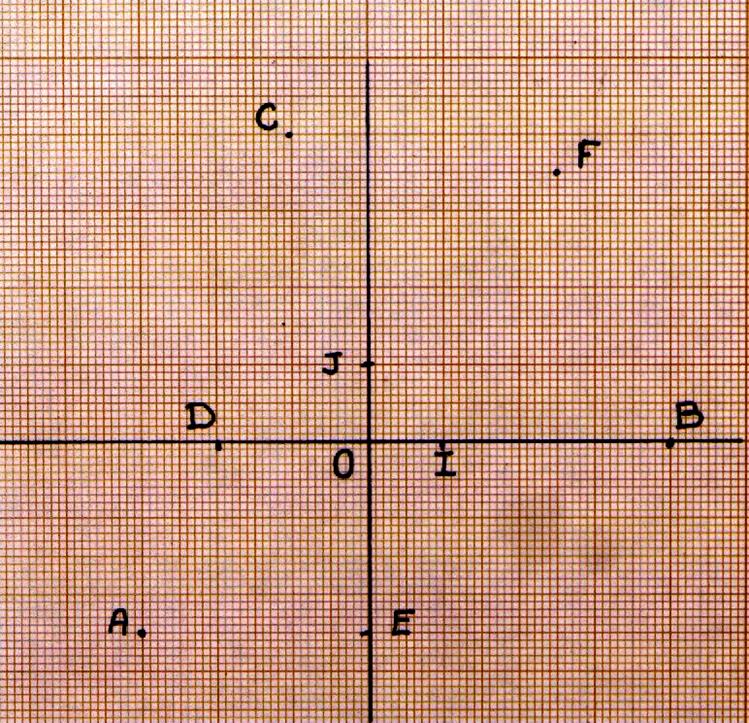
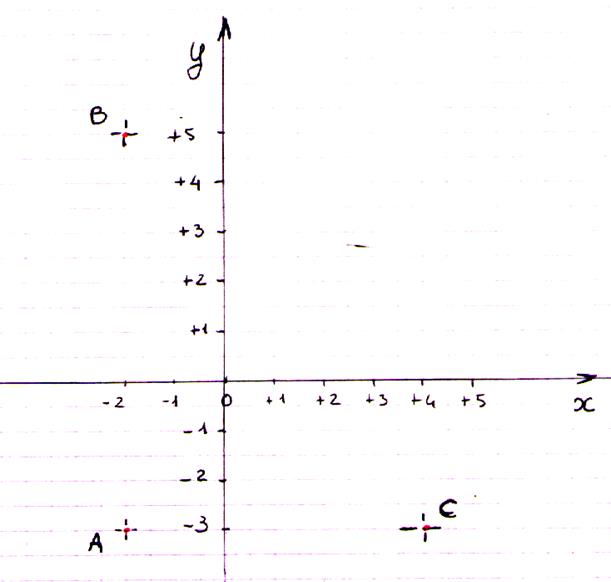
Exercice : Donner les
coordonnées des points A ;B ;C |
|
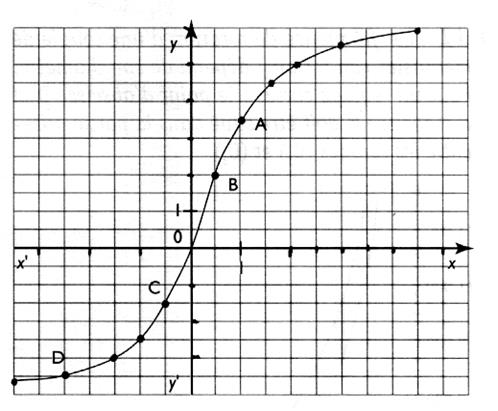
Activité 1 :
|
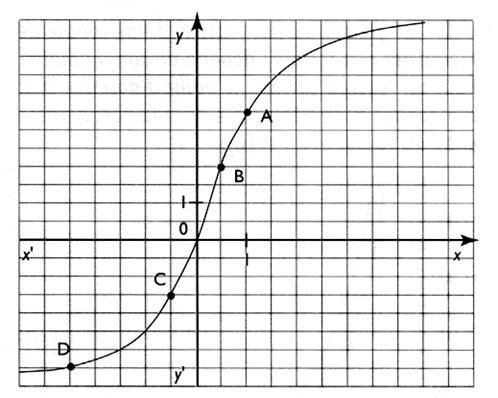
1°) Donner les coordonnées des
points : D ; C ; O ; B ; A. 2°) Quelle est l'ordonnée du
point de la courbe d'abscisse 3 ? 3°) Quelle est l'ordonnée du
point de la courbe d'abscisse -1,5 ? 4°) quelle est l'abscisse du
point de la courbe d'ordonnée +5 ? 5°) quelle est l'abscisse du
point de la courbe d'ordonnée -2, 5 ? |
|
|
|
|
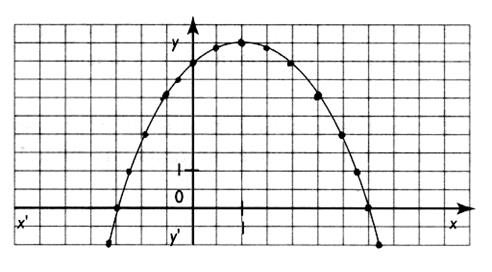
Activité :2
|
1°) Relever sur le tracé ci contre les coordonnées de tous les points et les
placer dans le tableau à double entrées ( ci dessous). |
|
|
|
|
|
|
|
D |
|
|
C |
O |
B |
A |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
2°) Sur une feuille blanche , tracer un repère cartésien
orthogonal ; le graduer [OI] =
Reporter les points ci-dessus et tracer la courbe .
Activité 3:
|
Faire
comme ci-dessus. - Construire un tableau et
donner les coordonnées des 15 points marqués. - Reproduire cette courbe sur
une feuille . |
|
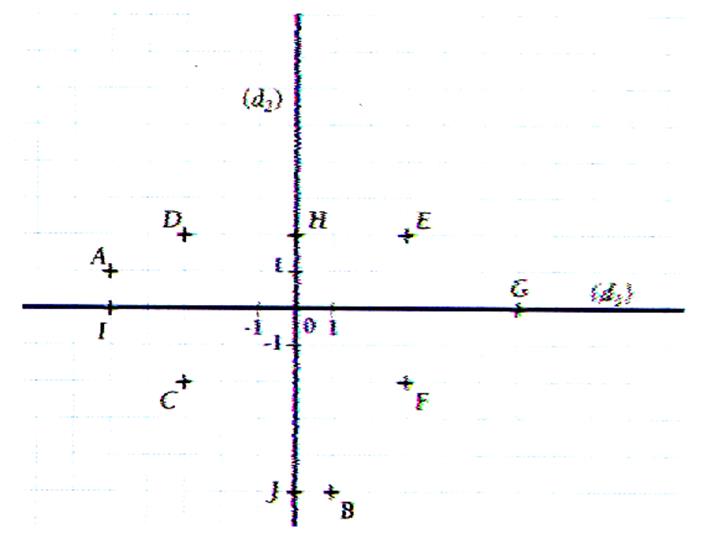
Exercice : Donner les coordonnées de tous les points .
|
|
|
Pour placer les villes de France, on trace sur la carte de France un
repère orthonormé (x ; y) d’origine Paris. L’unité est le côté d’un
carreau et quatre carreaux représentent
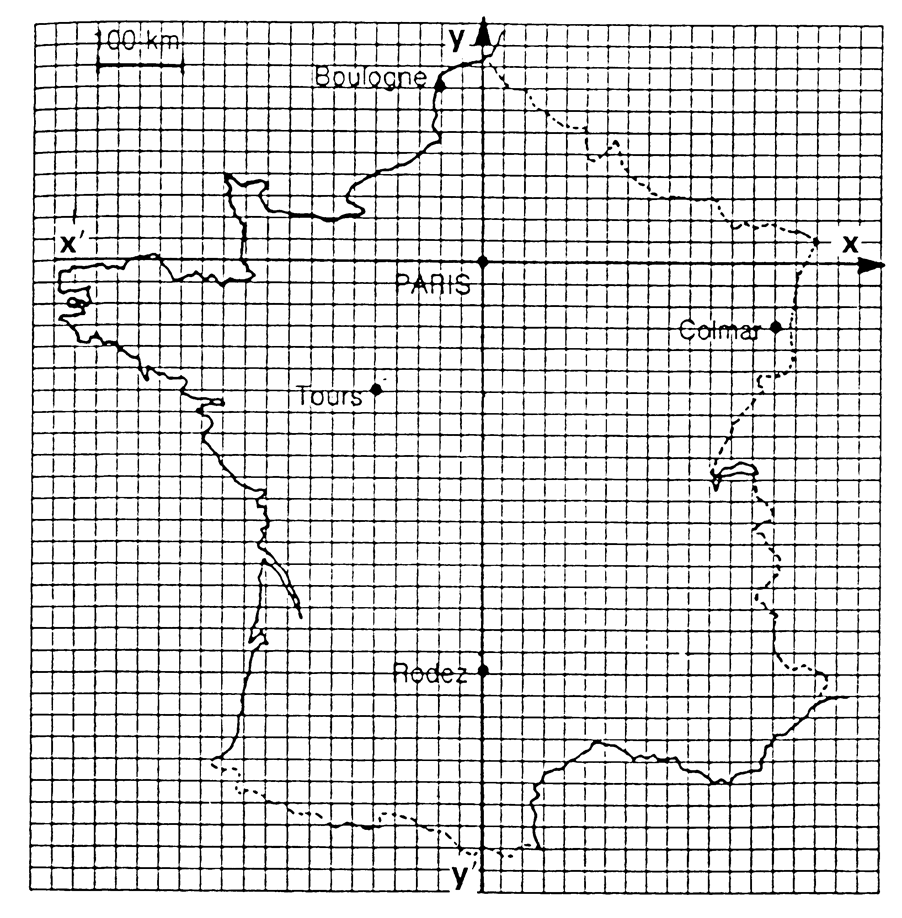
Parmi les quatre autres villes
présentes sur la carte, une seule fait l’objet d’un bon repérage, il s’agit
de :
1.
Boulogne -50 ; 200)
2.
Colmar (350 ; 75)
3.
Tours (-150 ; -125)
4.
Rodez (-475 ; 0)