|
Droite définition |
|
|
Repérage cartésien |
|
|
Repérage d’un point dans un repère |
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : 1°)Représentation graphique d’une fonction affine . 2°)
représentation d'une fonction linéaire. 3°)
Résumé sur les recherches des caractéristiques d’une droite. |
|
|
|
|
|
|
|
|
DOSSIER INFO : LES
DROITES dans un repère cartésien: Découverte : Représentation graphique d’une droite
croissante ; décroissante ; constante. |
|
|
|
|
|
|
|
|
|
-
L’axiome d’ Euclide. |
|
|
|
|
-
Les différentes
positions de droites dans un repère. ( par
rapport à l’axe). |
|
|
|
|
-
LES
DROITES « Croissantes » ,
« décroissantes » et « constantes » . |
|
|
|
|
|
|
|
|
TEST |
COURS
|
|
|
|
|
COURS |
|
|
|
|
|
|
|
|
|
Commentaire : A
partir de l’axiome d’Euclide : par deux points passe une seule
droite. Donc si je place deux points
dans un repère je peux tracer une
droite. |
|
|
|
|
|
|
|
|
|
Les différentes positions de droites dans un
repère. |
|
|
|
|
|
|
|
|
|
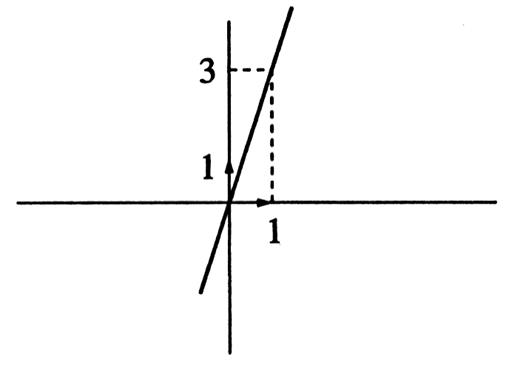
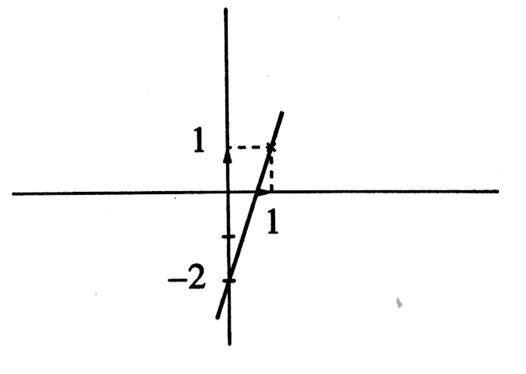
Cette droite peut « monter » de bas gauche au haut droite. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
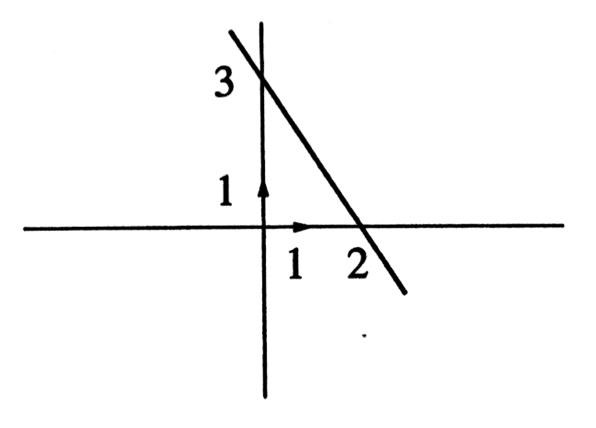
Cette
droite peut descendre du haut gauche au bas droite
|
|
|
|
|
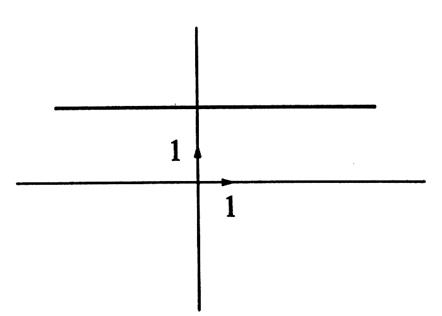
Cette
droite peut être parallèle à l’axe des « x »
|
|
|
|
|
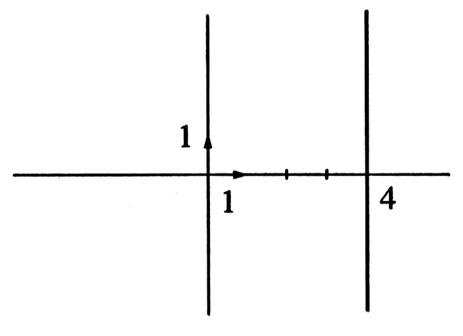
Cette
droite peut être parallèle à l’axe des « y » :
|
|
|
|
|
|
|
|
|
|
On
étudiera 2 cas : Cette
droite passe par « zéro » ou
ne passe pas
par « 0 », en montant
en descendant @ ;… |
|
|
|
|
|
|
|
|
|
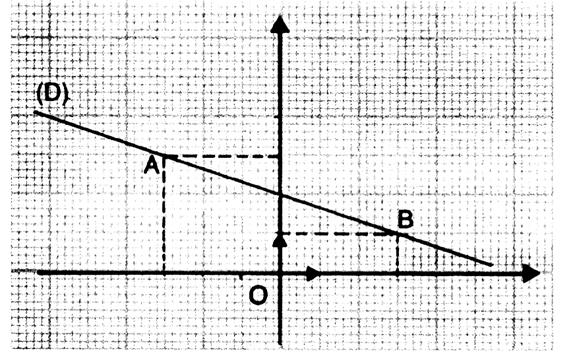
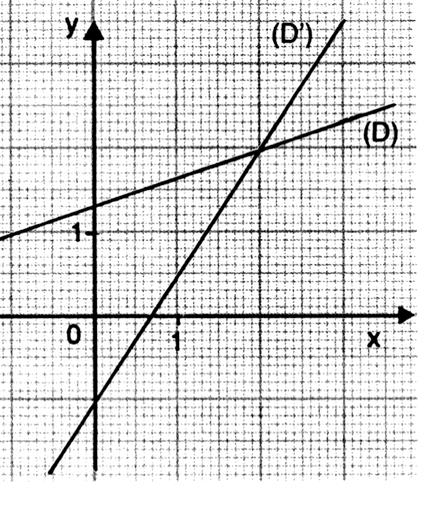
Exemple : La droite ( D ) est décroissante ; Nota : elle ne passe pas
par « 0 » (origine) du repère. |
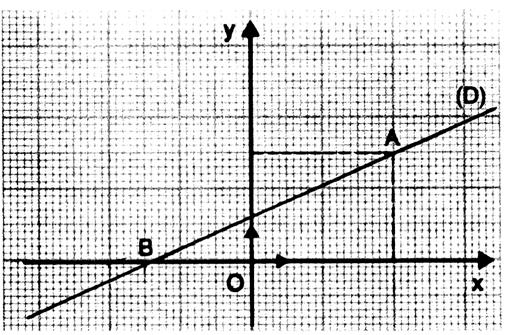
Exemple : La droite ( D ) est croissante , Nota :
elle ne passe pas par « 0 » (origine) du repère. |
|
|
|
|
|
|
|
|
|
|
|
|
|
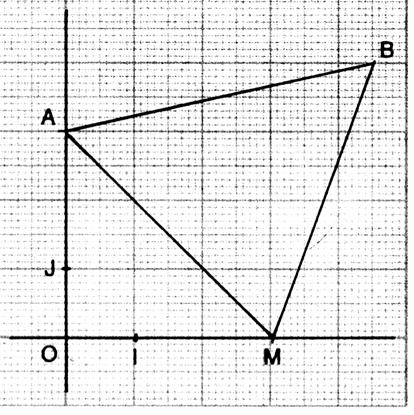
Exemples : Les 2
droites sont : L’une : croissante |
Exemple : 2 droites sont croissantes (
droite passant par AB et droite
passant par MB ) et une seule est décroissante (
droite passant par AM ) , elles ne passent pas par « 0 » (origine) du
repère. |
|
|
|
|
|
|
|
|
|
|
|
|
|
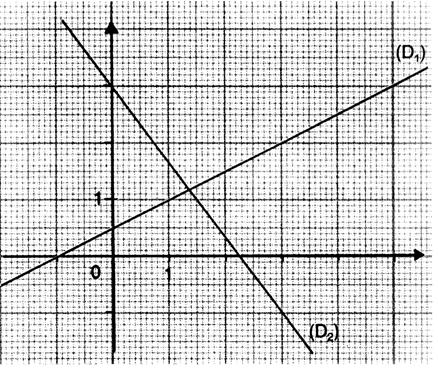
Les deux droites sont croissantes, elles se coupent en un point, elles
ne passent pas par « 0 » |
Les deux droites sont décroissantes , elles
se coupent en un point, elles ne passent pas par « 0 » |
|
|
|
|
|
|
|
|
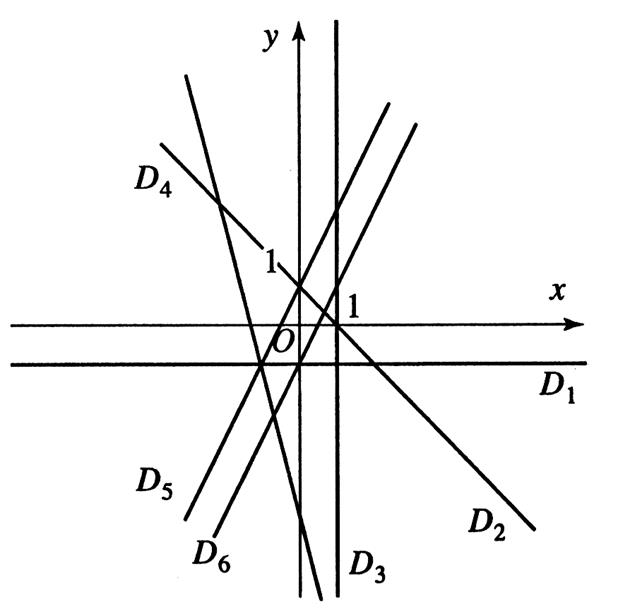
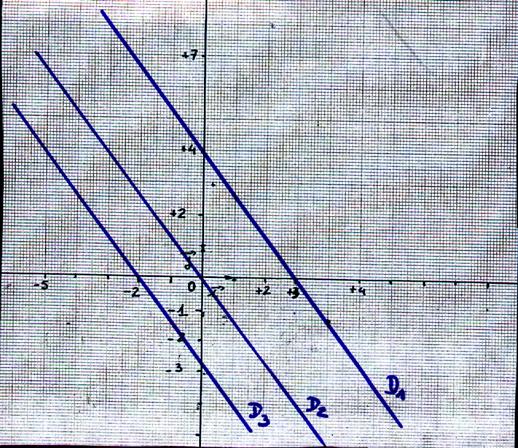
Dans le repère ci-dessous |
|
|
|
|
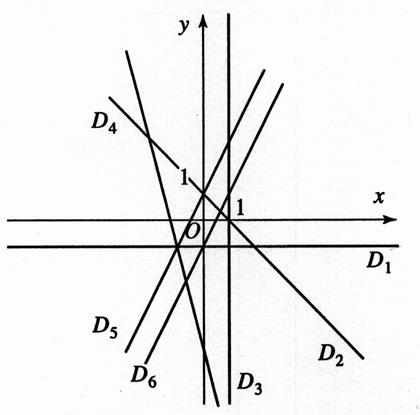
On identifie 6 droites . On remarque que : D4 et D2 sont décroissantes, D5 et D6 sont croissantes , elles sont parallèles. D1 est parallèle à l’axe des « D3 est parallèle à l’axe
des « |
|
|
|
|
|
|
|
|
|
LES DROITES « Croissantes » , « décroissantes » et
« constantes » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
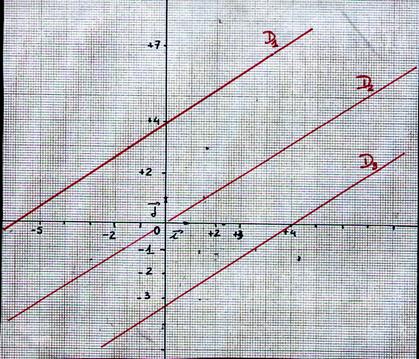
On dit qu’ elles sont
décroissantes : (D1 ; D2 ;D3
sont des cas particuliers parce qu’elles sont parallèles) Toutes les droites D1 et
D3 (sauf D2)
sont des droites dites « affines »
décroissante . Elles ont une équation de la forme : y = ax +b Cas particulier : les droites passant par O |
|
|
|
|
|
|
|
|
|
CONSTANTES :
dans un système d’axes on dit que les
droites sont dites
« constantes » si
elles sont parallèles à un des axes
.
|
|
|
|
|
|
|
|
|
|
·
D3 est parallèle à l’axe des « « k » est un nombre réel quelque soit la valeur de y . pour
D1 : x = k1 ·
Les droites D1 et D2 sont parallèles à l’axe des « x » Elles
ont pour équation : y = k
; « k » est un nombre réel quelque soit la valeur de y . pour D2 : y = k2 ; pour D1 : y = k1 |
|
|
|
|
|
|
|
|
|
CROISSANTE : Par
rapport au système d’axes, on dit que
ces droites « montent » si elle partent du « bas gauche » et se dirige vers le
« haut droit »
|
|
|
|
|
|
|
|
|
|
On dit qu’ elles sont
croissantes : (D1 ; D2 ;D3
sont des cas particuliers parce qu’elles sont parallèles) Toutes
les droites D1 et D3 (sauf D2) sont des droites dites « affines » croissante . Elles ont une équation de la forme : Cas
particulier : les droites passant par O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Dans
la représentation graphique : 1°
) Quand dit –on que droite est
croissante ? 2
° ) Quand dit –on que droite est décroissante ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EVALUATION
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|