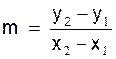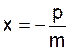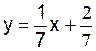Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
2°) Voir les
fiches 3ème collège. |
APRES : 1°) Les droites croissante ; décroissante,.. 2°)le parallélisme et la
perpendicularité |
Complément d’Info :
|
|
|
TITRE : ETUDE D’ UNE DROITE DANS
UN REPERE: Résumé. |
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
|||||
|
Interdisciplinarités : (matière concernée) |
|||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique
|
Physique Chimie Electricité |
Statistique. |
|
|
Pour en savoir plus : Pour chaque chapitre
il y a un retour au cours , il faut cliquer sur « info + »
|
|
COURS |
|
|||||
|
|
Dans tout ce qui suit le plan est muni d’un
repère ( |
|
|||||
|
|
|
||||||
|
|
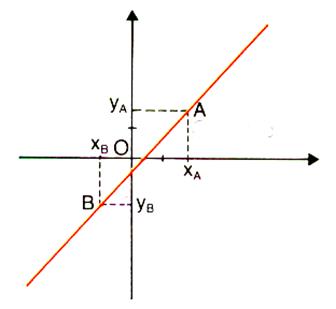
Soient «
Tous les points
du plan dont les coordonnées ( Par définition : Réciproquement : Si un point est sur (D) alors ses coordonnées vérifient l’égalité
|
|
|||||
|
|
Exemples : |
|
|||||
|
|
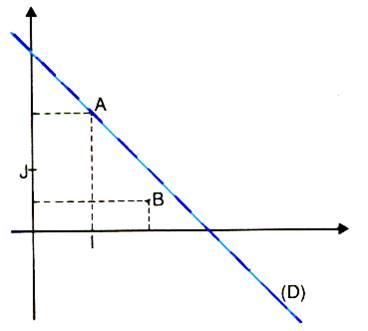
La
droite (D) a pour équation « A » appartient à (D) : « A » a pour coordonnées ( « B » n’appartient pas à ( D) : B a pour coordonnées ( 2 ;
«
|
|
|
||||
|
|
|
|
|||||
|
|
Tous les points du plan dont les coordonnées ( |
|
|
||||
|
|
Autre cas particulier : droite parallèle à
(OI) : Tous les points du
plan dont les coordonnées ( A vous de faire le tracer , dans un
repère ! ! ! |
|
|||||
|
|
|
|
|||||
|
|
II) RECHERCHE D’UNE EQUATION DE DROITE . |
|
|||||
|
|
|
|
|||||
|
|
Cas général : La droite n’est pas parallèle aux axes des ordonnées et abscisses . Toute droite ( ( on l’écrit ,aussi, sous la forme « Le nombre qui remplace « Le nombre « |
|
|||||
|
|
Remarque : il faut connaître la procédure « a)
On
connaît un point de la droite et son coefficient directeur. b)
Soit : Procédure : L’équation cherchée est de la forme « Commentaire 1 : On connaît « On remplace dans l’équation «
« « « Tel que l’ on obtient
Commentaire 2 : on connaît les valeurs de
« On remplace les valeurs
connues dans l’équation : On
transforme et on calcule pour en déduire la valeur de «
(le calcul terminé , il
suffit de remplacer « p » dans l’équation de départ par la valeur trouvée) |
|
|||||
|
|
a)
On
connaît deux points appartenant à la droite. On connaît deux points
de la droite : Soit A ( x1 ;
y1) et B( x2 ;
y2) les points donnés. Procédure : 1°) On calcule
« m » : tel que 2°) commentaire :
On connaît « m » , on se fixe (choisi) un
point « A » ou « B » , On connaît les coordonnées d’un point
et la valeur du coefficient « m », on se retrouve dans la
situation précédente, on termine par la procédure vue précédemment. |
|
|||||
|
|
Cas particulier 1 : Droite parallèle à l’axe des abscisses. Si « m » = 0 l’équation « y = m x +p »
devient y = p la droite ( D) est
alors parallèle à l’axe des abscisses . Cas particulier 2 : Droite parallèle à l’axe
des ordonnées. Si
« y = 0 » l’équation « y = m x + p » devient 0 = m x + p ;soit « (Remarque : « - p/m » peut être
un nombre positif « P » ) Toute droite
( D) qui
admet pour équation ,la
forme x = P , est
parallèle à l’axe des ordonnées. APPLICATIONS : classe de 3ème INFO : il y a 2
problèmes peuvent être proposés : soit que les coordonnées sont données , dans
l’énoncé , ou on demande de rechercher
,ces coordonnées, à partir d’une représentation graphique, sur une droite
tracée dans un repère . |
|
|||||
|
|
|
||||||
|
|
( 3 cas
sont présentés ) |
|
|||||
|
|
Cas 1 : On a deux points. |
|
|||||
|
On connaît les coordonnées de deux points A et B de (D)
. Procédure : On place
les points A et B et l’on trace ( D). |
|
||||||
|
|
|
||||||
|
Cas 2 : on connaît une équation. |
|||||||
|
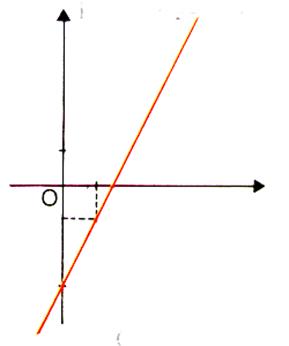
On connaît une équation de la droite (D) de la forme y = m x + p Exemple : y = 2x –3 Procédure : 1-
On place le point de coordonnée ( 0 ; p) Exemple : ( 0 ;
3) 2-
On place le point de coordonnées ( 1 ; p + m) Exemple : ( 1 ; 2 3-
On trace la droite qui passe par ces deux points |
|
||||||
|
|
|
|
|
||||
|
|
Cas 3 : on connaît un point et le
coefficient directeur. |
|
|||||
|
|
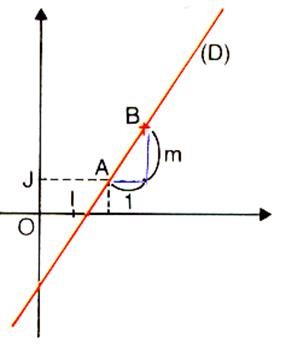
On connaît un point « A » et le
coefficient directeur « m ». Procédure : 1-
On place le point
« A »* 2-
On calcule les coordonnées du point
« B » : tel que xB =
(xA +1) et yB
=(yA+m) soit l’ exemple B ( + 3 ; 3-
place le point
« B » . 4-
on trace la droite
(D) passant par ces deux points. |
Exemple : A ( 2 ;
1 ) et m =
|
|
||||
|
|
|
|
|
||||
|
|
En conclusion : En
règle générale pour tracer une droite il faut donc chercher les coordonnées
de deux points . |
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
||||||
|
|
|
|
|
||||
|
|
Le coefficient directeur est un nombre relatif. Le coefficient directeur « m » ou « a » d’une droite indique comment varie l’ordonnée d’un point de la droite (D) si son abscisse augmente
de « 1 ». Si le repère
( O ; I ; J ) est
orthonormal : La valeur absolue du coefficient directeur est égal
à la tangente de l’angle aigu formé
par la droite ( D ) et l’axe des abscisses . Remarque : le coefficient directeur peut être positif ou négatif., le calcul du coefficient est donné par la
relation ( formule) suivante : Remarques : Les
nombres intervenant dans le calcul
étant des nombres « relatifs » , il
faudra être attentif au résultat des deux soustractions : « y2 - y1
=…. » et « x2 - x1 =….»
(signes) puis au résultat du quotient.
(le signe de « Que l’on note : |
|
|||||
|
|
|
|
|||||
|
|
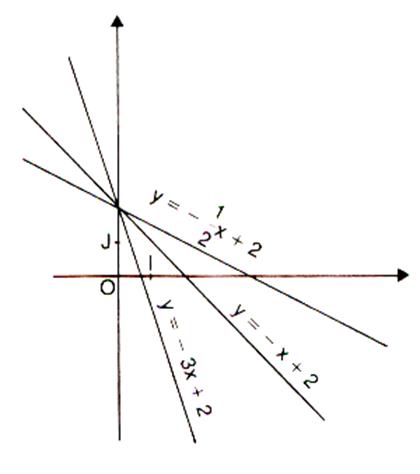
Droites croissantes. |
Info plus !!! et Info 2 +++ |
|
||||
|
|
Cas m
> 0 Si « m » est positif ; la droite est dite
croissante. Quand « x »
grandit ; « y » grandit . |
|
|
||||
|
|
Décroissantes. |
|
|||||
|
|
Cas m
< 0 Si « m » est négatif ; la droite est dite
« décroissante ». Quand « x »
grandit ; « y » diminue. |
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
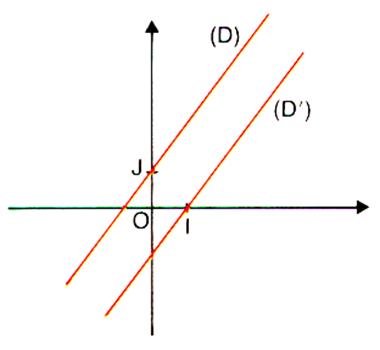
Deux droites (D) et (D’) sont parallèles
lorsqu’elles ont le même coefficient directeur . ( D) ; y = m x + p ( D’) ; y’ = m’ x + p’ (D) // ( D’) si m
= m’ |
|
|
||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
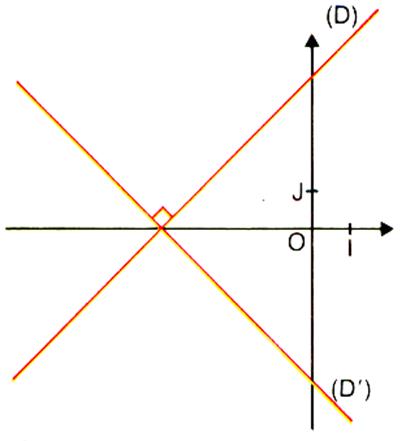
Le repère doit être orthogonal
. (ce qui est généralement
jusqu’à la fin du lycée) Deux droites
( D) et ( D’)
,(non parallèles aux axes), sont orthogonales lorsque le produit de
leur coefficient directeur est égal à –1 . Ainsi : ( D) ^ (D’) si m |
|
|
||||
|
|
|
|
|||||
|
|
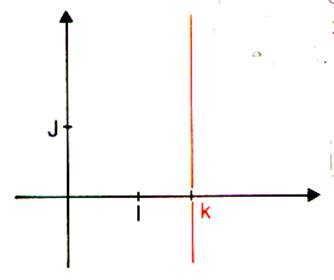
Remarque : La droite
d’équation : x = k est
parallèle à l’axe des ordonnées . La droite
d’équation : y = p est
parallèle à l’axe des abscisses . Les deux
droites d’équations : x = k et y
= p sont orthogonales si le repère
l’est aussi . |
|
|||||
|
|
|
|
|||||
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
|
|
|
|
1°) Par définition quelle est la forme de
l’équation d’une droite (D) ? 1°)
Compléter les phrases : a) Tous
les points du plan dont les coordonnées ( x , y )
vérifient l’égalité :
y = m x + p , sont ………………………………………….. b) Si un
point est sur (D) alors …………………………………………………… c) x = k
est l ‘équation d’une : ……………………………………………….. d) y = p
est l’ équation d’une ………………………………………………….. 2°) dans l’équation de la forme « y = ax +b » quel nom donne -
t-on à « a » et à « b » 3°)
Donner la procédure permettant d’établir l’équation d’une droite dont on
connaît : On connaît un point de la droite A ( x1 ; y1) et son coefficient directeur « m ». 4°)Donner la procédure
permettant d’établir l’équation d’une droite dont on
connaît deux points appartenant à la droite. 5°) Soit l’équation de la forme « y = m x +
p » si « m = 0 » que faut - il
conclure ? 6°) Soit l’équation de la forme « y = m x +
p » si « y = 0 » que faut - il conclure ? (on posera
« - p/m = P » 7°) En règle générale, que faut
-il connaître , au plus simple , pour tracer une droite dans un
repère ? 8°) Qu’indique le coefficient directeur d’une droite ? 9°) Compléter la phrase : La valeur absolue du coefficient directeur est égale
…………………………………………………………………………………………. 10°) Quel est la nature du nombre représentant le
coefficient directeur d ‘ une droite ? 11°) Quelle est la formule qui permet de calculer
le coefficient directeur d’une droite : 12°) si
m > 0
, que peut - on conclure ? 13°) si
m < 0 , que peut -on conclure ? 14°) On nous donne deux équations de droite.
Quand peut on dire que ces deux droites sont
« parallèles » ?: 15°) On nous donne deux équations de droite.
Quand peut on dire que ces deux droites sont
« perpendiculaires ou orthogonales » et non parallèles aux
axes ? |
|
|
|
|
|
|
|
1.
Dans un repère orthonormal,
on considère les courbes
suivantes : (C1 ) :
y = -2x +1 ; (C2 ) : y = x² + 3 y² = 5 ; (C3
) : y = 7x ; (C4 ) : y = x y + 3 x = 0 ; (C5
) : y = 5 ; (C7) : y = 3x + 6 y - 10 = 0 Parmi ces courbes, quelles sont celles qui sont
les représentantes d’une droite ? 2 . Dans un repère orthonormal , soit la droite
(D) : y = 6 1,5 x + 2,5 Dire si
les points suivants appartiennent à la droite (D) : A (
2 ; - 5) ; B ( 0,2,5 ) ; C ( -1 ; -1 ) et F
(-6 ; 5 ) 3 . Dans un repère orthonormal, on considère les droites : D1 : y = 2x + 5 ; D2 : y =
- 3 x + 8 ; D3 :
y = x - 7 ; D4 :
y = - x + 1 Déterminer
le coefficient directeur de chacune de ces droites 4. Dans un repère orthonormal ,
soit la droite ( D) : y = -0,5 x
+ 2 a)
déterminer les ordonnées des points A ; B ; C et D d’abscisses
respectives : 1 ; 4 ; -7 et -2 b) Déterminer les abscisses des points E ;
F ;G et H d’ordonnées respectives :
1 ; 4 ; -7 et -2 5 . Dans un repère orthonormal , tracer les
droites : (D 1 ) de coefficient directeur « -1 » et passant par le point de
coordonnées ( 0 ; 2 ) ; (D 2 ) de coefficient directeur « 0,5 » et passant par le point
de coordonnées ( 0 ; -1 ) (D 3 ) de coefficient directeur « -1,5 » et passant par le point
de coordonnées ( 1 ; -3 ) (D 4 ) de coefficient directeur « 2 » et passant par le point de
coordonnées ( -1 ; 1 ) 6. . Dans un repère orthonormal, tracer les droites : D1 : y = 2x + 5 ; D2 : y =
- 3 x + 8 ; D3 :
y = x - 7 ; D4 : y =
- x + 1 7. Dans un repère orthonormal ,
déterminer une équation de la droite ( D) passant par le point A ( 0 ; 5
) et B ( -2 ; 3 ) 8 . Dans un repère orthonormal , déterminer une équation de la droite ( D) passant par
le point A ( - 1 ; 4 ) et dont le coefficient directeur est « m = -4 ». 9. Déterminer une équation de chacune des droites
( D 1 ) ; ( D 2 ) et
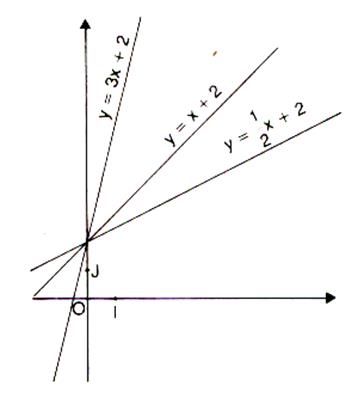
( D 3 ) données dans le repère orthonormal ci contre. 10. Dans un repère orthonormal
, soit la droite ( D) dont une
équation est y = 3x + 5 . Parmi les droites suivantes : D1 : y = 3x + 2 ; D2 : y =
3 x + 0,5 ; D3 : y =-3 x + 0,5 ; D4 : y =
0,5 x + 4 Quelles sont celles qui sont celles qui sont
parallèles à la droite ( D) ? 11. Dans un repère orthonormal, soit la droite ( D) dont une équation est « y = 3x +5 » parmi les droites suivantes : D 1 : Quelles sont celles qui sont perpendiculaires à
la droite ( D) . ? |
|
|
|
|
|