Pré requis:
|
|
|
|
|
ENVIRONNEMENT du dossier:
DOSSIER : Position de deux droites.
a) Comment reconnaître le parallélisme. ?
b) Comment reconnaître l’orthogonalité ?
c) Applications.
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
|
|
|
Deux droites peuvent être : parallèles ou sécantes.
Deux droites parallèles
peuvent être disjointes ou superposées (confondues).
Deux droites sécantes
peuvent être perpendiculaires.
Les
équations des deux droites concernées peuvent nous permettent de montrer par le
calcul ou l'analyse des valeurs données "a" et "b" quelle est la position
géométrique de ces deux droites, l'une par rapport à l'autre..
I ) DROITES PARALLELES
|
Propriété : |
|
|
Les deux droites sont parallèles si et seulement
si elles ont même coefficient directeur. |
|
Activité 1 : pour reconnaître
le parallélisme :
Pré –requis : reconnaître deux
droites sécantes ;
parallèles ou confondues. E t Positions
relatives de
deux droites
Activité: Tracer les trois
droites (D1) ; (D2) ;
(D3) ; suivantes données par leur équation de la forme : y
= m x + p
|
(D1) |
(D2) |
(D3) |
|
y
= 2 x + 1 |
y
= 3x - 4 |
y
= 2x- 4 |
Compléter le tableau ( mettre
une croix dans la case correspondante) ; quelles sont leur position
relative (autrement dit : comment sont-elles l’une par rapport à
l’autre ?)
|
|
Sécantes ? |
Parallèles ? |
Confondues ?
(donc parallèles) |
|
(D1) et (D2) |
|
|
|
|
(D1)
et (D3) |
|
|
|
|
(D2)
et (D3) |
|
|
|
Résumé
:
Pour que deux droites soient parallèles il faut et il suffit qu'elles
aient le même coefficient directeur .
Deux droites y = ax +
b et
y = a'x +b' seront parallèles si elles sont
parallèles à la même droite y = ax .
D'où la condition a = a'
Exemples :
y = 3x + 2 et y = 3x -5 , elles sont parallèles « a = 3 »
et y = - x - 2
et y = - x + 7 ; elles sont
parallèles « a = -1 »
II ) Droites
perpendiculaires
|
Deux
droites perpendiculaires forment un angle droit . |
|
|
A retenir : Pour que deux droites soient perpendiculaires
il faut et il suffit que leurs coefficients directeurs aient pour
produit -1.
|
|
Exemple : Dans un repère orthonormée , tracer
les deux droites suivantes :
D1 : « y1 = 3x +
5 » et D 2 : 
Avec un rapporteur, mesurer l’angle que font les
deux droites.
(elles forment un angle droit)
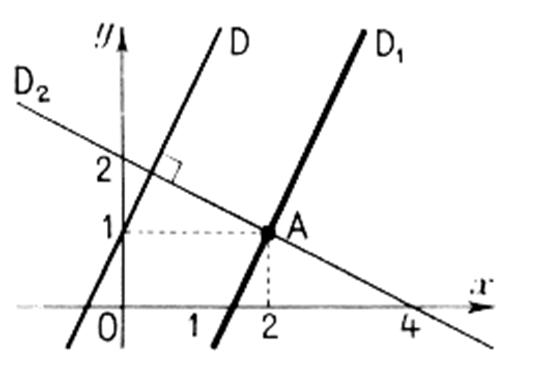
Les deux droites « y = a x + b » et
« y = a ' x + b' » seront perpendiculaires s'il en est de même de
leurs parallèles « y = a x » et « y = a' x »
Ces parallèles issues de O (voir figure ci -
dessus) sont définies par les points A ( 1 ; a ) et A' ( 1 ; a' ) .
La condition : 
² + 
² = 
² est
nécessaire et suffisante pour que le triangle O A A' soit rectangle en O (en
supposant que l'unité de longueur est la même sur les deux axes.)
(pré requis : distance de deux points dans un repère)
Applications:
|
·
Déterminer l'équation de la parallèle
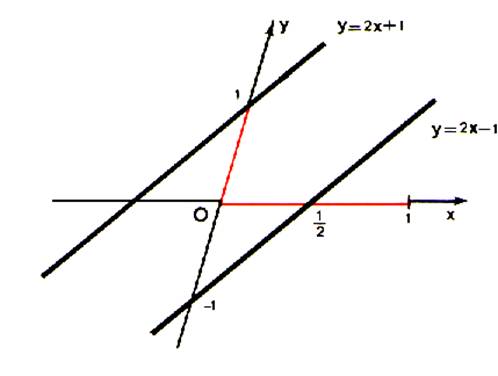
et l'équation de la perpendiculaire menées du point A ( 2 ; 1 ) à la
droite ( D ) d'équation y = 2x +1 |
|
1°) La parallèle D1 à D a une équation
de la forme y = 2x + b
.
En écrivant qu'elle passe par A ( 2 ; 1 ) , on
obtient : 1 = 4 + b , donc b = -3
L'équation de la droite D1 est donc : y = 2 x - 3
2°) la perpendiculaire D2 à D a une équation de la forme y = -
x
+ b' .
En écrivant qu'elle passe par A ,
on obtient 1 = -1 + b ' , donc b' = 2 . D'où l'équation de la perpendiculaire
D2 = y
= - 
+ 2
TRAVAUX AUTO - FORMATIFS et DEVOIR FORMATIF:
1°) On donne deux équations de droites
, pour quelle condition peut -on
dire que deux droites sont
parallèles ?
2°) On donne deux équations de droites
, pour quelle condition peut -on
dire que deux droites sont
perpendiculaires ?
Pré requis
1.
Dans un repère orthonormal,
on considère les courbes
suivantes :
(C1 ) : y
= -2x +1 ; (C2 ) : y = x² + 3 y² = 5 ; (C3
) : y = 7x ; (C4 ) : y = x y + 3 x = 0 ; (C5
) : y = 5 ; (C7) : y = 3x + 6 y - 10 = 0
Parmi ces courbes, quelles sont celles qui sont les
représentantes d’une droite ?
2 .
Dans un repère orthonormal , soit la droite (D) : y = 6 1,5 x + 2,5
Dire si les
points suivants appartiennent à la droite (D) :
A (
2 ; - 5) ; B ( 0,2,5 ) ; C ( -1 ; -1 ) et F
(-6 ; 5 )
3 .
Dans un repère orthonormal, on considère les
droites :
D1 : y = 2x + 5 ; D2 : y = -
3 x + 8 ; D3 : y =
x - 7 ; D4 : y
= - x + 1
Déterminer le
coefficient directeur de chacune de ces droites
4 .
Dans un repère orthonormal , tracer les droites :
(D 1 ) de coefficient directeur « -1 » et passant par le point de
coordonnées ( 0 ; 2 ) ;
(D 2 ) de coefficient directeur « 0,5 » et passant par le point de
coordonnées ( 0 ; -1 )
(D 3 ) de coefficient directeur « -1,5 » et passant par le point
de coordonnées ( 1 ; -3 )
(D 4 ) de coefficient directeur « 2 » et passant par le point de
coordonnées ( -1 ; 1 )
5 .
Dans un repère orthonormal, tracer les droites :
D1 : y = 2x + 5 ; D2 : y = -
3 x + 8 ; D3 : y =
x - 7 ; D4 : y = -
x + 1
Fin du pré requis.
1. Dans un repère orthonormal , soit la
droite ( D) dont une équation est y = 3x
+ 5 . Parmi les droites suivantes :
D1 : y = 3x + 2 ; D2 : y = 3
x + 0,5 ; D3 : y =-3 x + 0,5 ; D4 : y =
0,5 x + 4
Quelles sont celles qui sont celles qui sont
parallèles à la droite ( D) ?
2. Dans un
repère orthonormal, soit la droite (
D) dont une équation est « y = 3x +5 »
parmi
les droites suivantes :
D 1 : 
; D2 = 
; D 3 = 
; D 4
= y = 3 x + 4
Quelles sont celles qui sont perpendiculaires à la
droite ( D) . ?