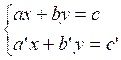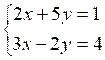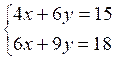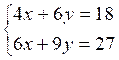|
|
|
|
Position relative
de deux droites |
|
|
Système d’équation
(définition) |
|
|
Equations de
droites : représentation graphique |
ENVIRONNEMENT du
dossier:
DOSSIER :
RESOLUTION
GRAPHIQUE d’un SYSTEME de deux EQUATIONS
du PREMIER DEGRE A DEUX INCONNUES
|
TEST |
COURS |
|
Corrigé Contrôle |
Corrigé évaluation
|
COURS
SYSTEME DE DEUX EQUATIONS A DEUX INCONNUES.
|
Un
système de deux équations à deux inconnues : Peut
toujours se ramener à la forme générale : a ;
b ;c ; a’ ; b’ ;c’ sont des nombres réels, « x »
et « y » sont les inconnues. Résoudre
un tel système , c’est rechercher les valeurs de
« x » et de « y » qui vérifient simultanément les deux
équations et « x » et « y » sont
les solutions ou « racines » du système. |
RESOLUTION GRAPHIQUE
|
pré
requis : voir "Repère orthonormé" |
Chaque équation du système est considérée comme l’équation d’une
droite .
On représente
chacune des droites dans un même repère.
La solution , si elle existe , est donnée par
les coordonnées du point
d’intersection des droites.
On obtient 3 types de
représentations graphiques :
|
1°) Les droites sont sécantes |
|
|
Droites
perpendiculaires |
|
|
2°) Les droites sont parallèles |
|
|
3°) Les droites sont parallèles et superposées |
|
1°) Cas : à une solution (classe 3e)
|
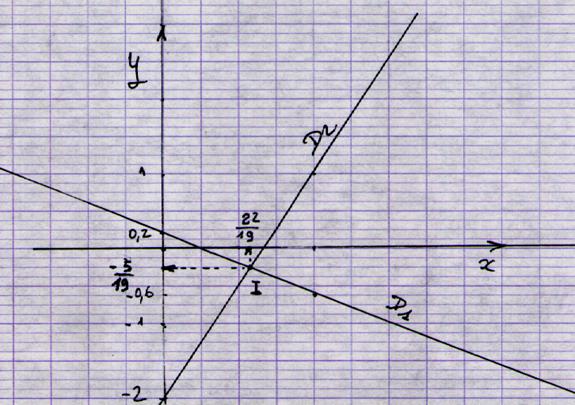
Les droites sont sécantes : |
Analyse des tracés : les deux droites se coupent,elles sont sécantes ! |
|
Soit le système : On transforme l’égalité (1) « 2x + 5 y =1 » en
équation de la forme y = en f(x) 5y = -2x+1 ; y = - 0,4 x +
0,2 on trace la droite D1 d’équation : y = - 0,4 x + 0,2 On transforme l’égalité (2) « 3x - 2y = 4 » en
équation de la forme y = f(x) -2y =
-3x+4 ; y = 1,5 x - 2 on trace la droite D2 d’équation : y = 1,5 x - 2 Voir « solution algébrique » : |
|
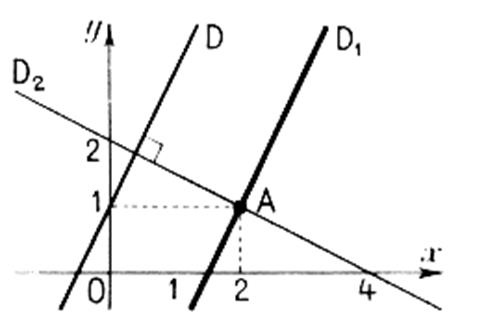
Cas particulier des droites sécantes :
|
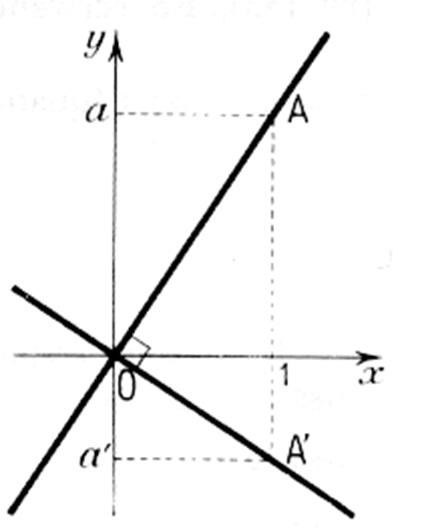
Droites perpendiculaires : |
|
|
Deux droites sont perpendiculaires si ……. |
|
|
Si le produit des coefficients
directeurs des deux droites est égal à « -1 » alors ces droites
sont perpendiculaires. |
|
2°)
Cas « impossible »
(aucune solution)
|
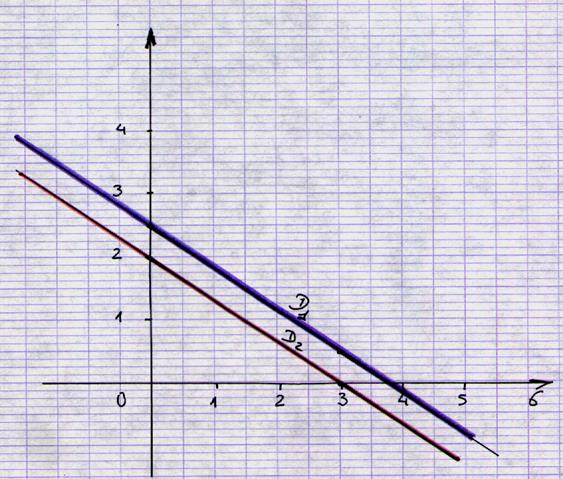
Analyse des tracés : Les deux droites ne se coupent pas, elles sont parallèles ! |
|
|
On transforme l’égalité (1) « 4x + 6 y =15 » en
équation de la forme y = f(x) 6y = - 4 x + 15 ; y = - on trace la droite D1 d’équation : y = - On transforme l’égalité (2) « 6x + 9 y = 18 » en
équation de la forme y = f(x) 9y = - 6 x + 18 ; y = - on trace la droite D2 d’équation : y = - |
|
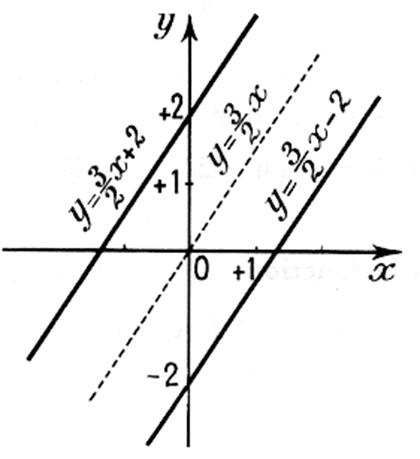
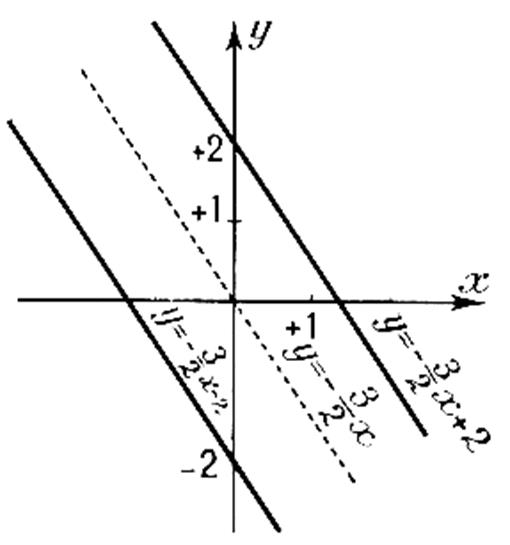
Exemples :
|
Remarquez : que deux droites parallèles ont le même coefficient
directeur. |
|
|
|
|
|
|
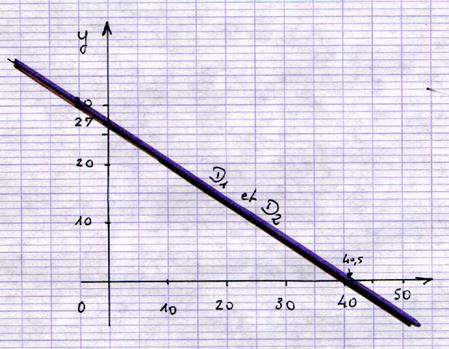
Analyse des tracés : Les deux droites sont
superposées ; le système est dit « indéterminé » |
|
On transforme l’égalité (1) « 4x + 6 y =18 » en
équation de la forme y = f(x) 6y = - 4 x + 18 ; y = - on trace la droite D1 d’équation : y = - On transforme l’égalité (2) « 6x + 9 y = 27 » en équation
de la forme y = f(x) 9y = - 6 x + 27 ; y = - on trace la droite D2 d’équation : y = - |
|
APPLICATION :
|
Commenter les tracés ci -contre : |
|
|
|
|
CONTROLE
Citer les 3 cas que l’on peut rencontrer lors de l’étude graphique d ‘un système de fonctions affines.(équations du premier degré à deux inconnues)
Systèmes d’équations du premier degré à deux inconnues : Représenté
graphiquement les 3 cas, dans un repère
cartésien.
Successivement , dans
un même repère cartésien:
|
Tracer
D1 et D2 |
Tracer
D3 et D4 |
Tracer
D5 et D6 |
|
|
|
|