Pré requis:
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
1°)La droite |
1°)Position relative de la droite et un plan |
DOSSIER : Positions relatives de
deux droites : (sécantes ;
parallèles ou confondues)
-
coplanaires ;
-
non coplanaires.
|
TEST |
COURS |
Interdisciplinarité
|
|
COURS
|
RAPPELS :
|
|
|
II
) 2 droites sont soit « sécantes » ;
soit disjointes (aucun
point commun ) ; soit
confondues ( tous les points
de l’une appartiennent à l’autre)
. nota :
si elles ne sont pas sécantes , elles sont parallèles. |
|
|
|
|
Notions : Droite coplanaire et droite non coplanaire
|
|
|
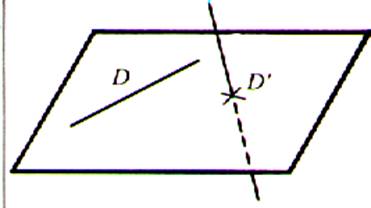
La droite D est coplanaire . ( elle a tous ses points confondus avec le plan) La droite D’ n’est pas coplanaire ( elle a un
seul point commun avec le plan) |
|
I
)Droite coplanaire
|
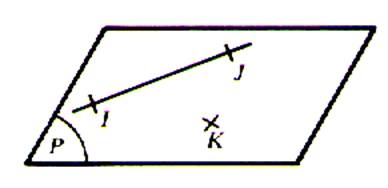
Les trois points
I ; J ; K sont dans
le plan P, La droite passe par les points I ; J . Cette droite est dite « coplanaire »
|
|
II
) Des droites sont
« coplanaires »
si elles se trouvent dans un même plan
|
|
|
|
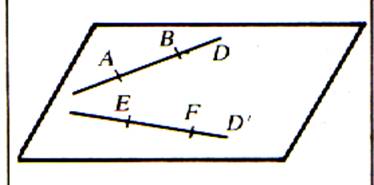
Les
4 points appartiennent au plan . -
La
droite D passe par les points A ; B -
La
droite D’ passe par E ; F . Les
deux droites D et D’ sont dans un même plan . Elles sont coplanaires. |
|
III
) Droites sécantes coplanaires :
|
En plus : Droites
parallèles dans un repère : |
D et
de D’ sont confondus avec le plan
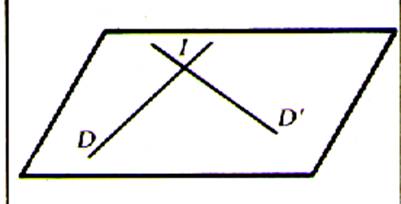
Les droites D et D’ sont
sécantes et coplanaires .
|
|
|
III ) cas
particulier : Droites sécantes
« perpendiculaires »
coplanaires |
|
|
D
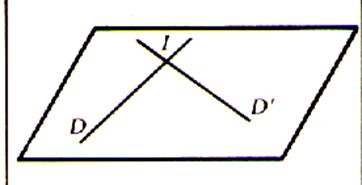
et de D’ sont confondus avec le plan Si les deux droites sécantes forment un angle
droit elles sont sécantes
perpendiculaires et coplanaires. |
|
I
V ) Droites parallèles coplanaires
|
|
|
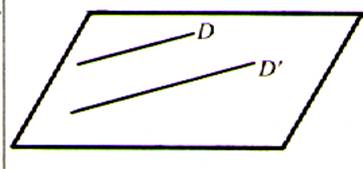
D
et de D’ sont confondus avec le plan Les
droites sont parallèles ; elles n’ont aucun point
commun . (elles sont coplanaires ) . |
|
|
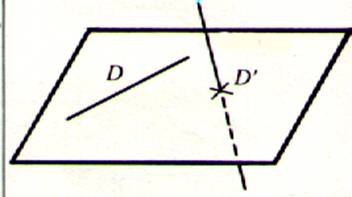
1°) Si la droite « D » n’a aucun point commun avec le
plan considéré ; la droite D n’est pas coplanaire. (dans le croquis on peut considéré
que D’ appartient au plan , M étant un
point du plan ; D et D4 sont parallèles ) |
|
|
2°) ) Droites non
coplanaires : |
|
|
Les
droites D et D’ n’ont aucun point
commun et elles ne sont pas coplanaires. D’ n’est pas coplanaire au plan
contenant la droite D. |
|
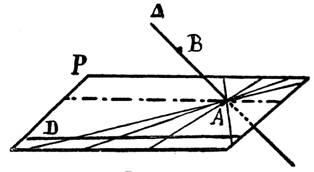
La
droite D n’est pas coplanaire ; elle est
oblique au plan P .
Ci dessous : La droite « delta » est oblique
au plan « P »
|
|
|
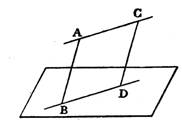
la
droite AC et parallèle à la droite BD qui cette droite appartient au plan . |
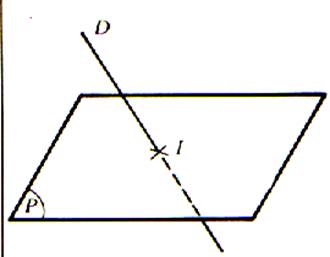
La
droite D n’est pas coplanaire ; elle est
parallèle au plan P.
|
|
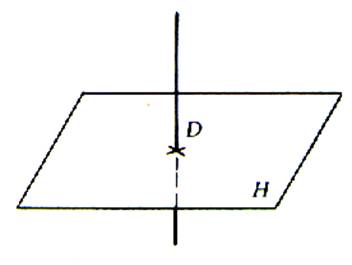
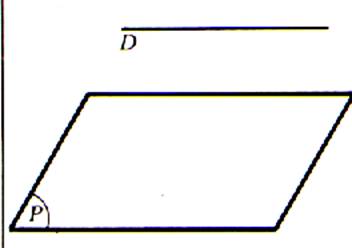
La
droite D n’est pas coplanaire ; elle est
perpendiculaire au plan H.
( projection orthogonales de « A »
et « B » ) sont confondus. |
|
TRAVAUX AUTO FORMATIFS :
Quand dit – on que deux droites sont :
1°) « Coplanaires »
2°) « non coplanaires » ( aidez vous d’un dessin)
parallèles
sécantes
sécantes coplanaires
perpendiculaires coplanaires
parallèles coplanaires
sécantes non coplanaires
perpendiculaires non coplanaires
parallèles non coplanaires
Dessiner avec des outils :
Sur une feuille deux
droites :
v
parallèles
v
sécantes
v
sécantes coplanaires
v
perpendiculaires coplanaires
v
parallèles coplanaires
v
sécantes non
coplanaires
v
perpendiculaires non coplanaires
v
parallèles
non coplanaires
A main levée ( en perspective) :
« non coplanaires » (
aidez vous d’un dessin)
sécantes non coplanaires
perpendiculaires non coplanaires
parallèles non coplanaires

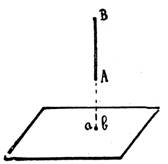 la
droite AB est perpendiculaire au plan . « a » et « b »
la
droite AB est perpendiculaire au plan . « a » et « b »