Pré requis:

Notions préliminaires
Ligne droite (notion)

ENVIRONNEMENT du dossier:

Index « warmaths »

Objectif précédent : 1°) vue en primaire. 2°) Droite passant par un ou plusieurs points

Objectif suivant : 1°). Droite –demi droite- segment : vu en 6^ème collège 2°) La demi – droite. 3°) Positions relatives de deux droites. 4°) Droites dans un plan.

Info 1 : Liste des cours en géométrie. Info 2 : Tableau

DOSSIER : LA LIGNE DROITE :

1. Notions .
2. Les propriétés et axiome d’Euclide. Et la conséquence .
3. « droite illimitée »,  « demi- droite ( ou semi -droite) », « segment de droite ».
4. Notations symbolique d’une droite .
5. La droite :son tracé.
6. les principaux noms des droites utilisées en géométrie : médiane médiatrice ,…….
7. Positions relatives d’une droite et d’un point.
8. Position relatives de deux droites .

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Travaux dos.46	Corrigé Contrôle	Corrigé évaluation
				@ INTERDISCIPLINARITE

Info COURS

Notions : La droite est une courbe particulière !!!!!

Info +++

1°) Notions :La ligne droite
Exemples de ligne droite : Un fil fin et bien tendu , chaque arête d’une règle carrée , triangulaire , chaque bord d’une règle plate , un trait droite que l’on aura tracé en suivant le bord de cette règle sont des lignes droites . Au lieu de dire « ligne droite » , on dit souvent « droite ».
Activité : prendre une feuille de cahier ( c’est un plan) ; plier cette feuille . On obtient deux parties ( appelées « demi-plan ») . L’intersection de ces deux demi - plan forme un pli , la trace de ce pli est appelé : droite.
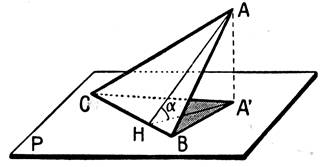
Une droite est obtenu par l’intersection de deux demi plans .	Nota Plier une feuille , le pli est une droite. Exemple : la droite passant par CB est obtenue par le pliage du plan passant par les points CAB et le plan passant par les points CA’B

a) Première propriété fondamentale de la ligne droite : que l’on appelle l’ axiome d ’ Euclide :
Par deux points distincts , on peut faire passer une ligne droite et une seule.
· Activité 1 :Considérons deux points « A » et « B » marqués sur une feuille de papier ( voir ci contre) plaçons une règle bien droite de façon que l’un des bords passe par ces deux points et traçons un trait au crayon en suivant le bord ; nous obtenons ainsi une ligne droite qui passe par les points « A » et « B ». · Activité 2 : Traçons à l’encre, et à l’aide du même procédé , un trait passant encore par les points « A » et « B » ; nous obtenons ainsi une ligne droite qui recouvre la première. Les deux droites dessinées passent par les deux points « A » et « B » et elles n’en font qu’une ; « elles coïncident »
Cette propriété nous apparaît comme une vérité première inséparable de l’idée de ligne droite. On énonce souvent cette propriété de la façon suivante : Deux points distincts déterminent une droite.
La ligne droite est un alignement de points placés dans la même direction ; rectiligne (voir objectif  Info ++sur « direction et sens » +) Vocabulaire : d’après le dictionnaire : « direction » : ligne suivant laquelle un corps se déplace . « rectiligne » : se déplace en ligne droite. L’outil couramment utilisé pour tracer une « droite » est une « règle ». (voir les différentes règles ................................................)
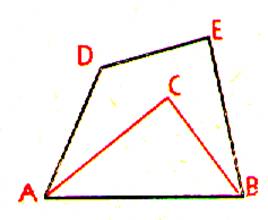
b) Deuxième propriété : Le plus court chemin d’un point à un autre est la ligne droite : D’après le croquis : la ligne droite AB est plus courte que la ligne brisée ADEB AB < ACB AB < ADEB Le signe « < »se lit : plus petit que
Voir @ INFO CD : les inégalités triangulaires
D’où ce que l’on appelle l’ axiome d ’ Euclide : Par deux point « A » et « B » passe une droite est une seule .
c) Conséquence : Si l’on sait que deux droites ont deux points communs, on peut affirmer que ces deux droites se confondent , c'est-à-dire qu’elles ne forment plus qu’une.
Activité 3 . : Tendons entre deux points A et B un fil rouge et un fil noir ; si nous faisons glisser les deux fils l’un sur l’autre , nous constatons que les deux fils coïncident sur toute leur longueur. « Par deux points, on peut faire passer une ligne droite et l’on ne peut en faire passer qu’une seule »

	Remarque importante : Lorsque l’on trace un trait rectiligne , il faut préciser par une notation précise si on a cherché à représenter une droite ; une demi- droite ou un segment.
	3°) La droite « illimité » ; « semi – droite » ; « segment de droite ».
	a) Droite illimitée -
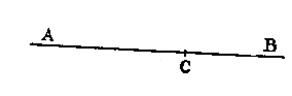
	Soit la droite AB (voir la figure ci-dessus, il faut la considérer comme « illimitée » dans les deux sens ; vers la droite , elle se prolonge indéfiniment et n’a pas de dernier point ; de même vers la gauche . C’est une droite que l’on peut aussi bien prolonger dans un sens que dans l’autre.  On dira que par exemple : ( x y ) est une droite illimitée
	b) Demi-droite : ( semi – droite)
	Activité : Plaçons un point O sur une droite illimitée. La portion de droite qui est limitée à gauche par le point O et qui est illimitée à droite de ce point est appelée : une demi-droite . Le point O est appelé « origine ». ( voir droite graduée).
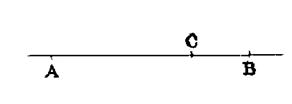
	D’où, lorsqu’un point « C » est situé sur une droite illimitée AB (ci contre ) , il la partage en deux portions « CA » et « CB » , situées de part et d’autre de ce point, et que l’on appelle « demi droites » ou « semi- droites » . La semi- droite « CA » commence au point « C » qui est appelé son « origine » et est illimitée vers la gauche . Quand deux semi –droites telles que « CA » et « CB » ont même origine « C » et forme à elles deux une droite illimitée « AB », on dit qu’elles sont le prolongement l’une de l’autre ; ainsi « CB » est le prolongement de « CA » et inversement. Remarque : Une demi – droite « CA » n’a qu’un seul prolongement.
	d) Segment de droite : (Info ++ sur le segment)
	Le segment de droite est une portion de droite illimitée ; comprise entre deux points (ces deux points sont appelés : bornes) On appelle encore ce segment : un segment rectiligne ; ci contre « AB » est un segment rectiligne . on le note : [ A B ]
	4°) NOTATION d’une droite : On peut notée de 3 façons une droite. soit : la droite « D » : notée : D (on nomme la droite par une lettre) ou la droite y x notée ( y x) (on place une lettre aux extrémités ) ou la « droite AB » notée (AB) ( on fait passer la droite par deux points)
	D x A B y

5°) TRACE de la ligne droite : Puisque par deux points on ne peut faire passer qu’une seule ligne droite , il suffira pour construire une droite de connaître le lieu de deux de ces points.
a) Tracé sur un tableau ou sur une feuille de papier : Le tracé se fait à l’aide d’une règle plate. Précaution : avant de se servir d’une règle il faut vérifier la rectitude de celle ci. Il faut vérifier si ses bords sont rectilignes. Vérification : on trace un premier trait AB , puis on retourne la règle en la faisant pivoter autour du trait et on trace un second trait ; si les bords de la règle sont rectilignes , les deux traits doivent se confondre. Si les deux lignes passant par AB ne coïncident pas , le bord de la règle n’est pas rectiligne Tracé : On détermine deux points de passage de la droite puis on fait passer le bord de la règle par les deux points donnés , on fait ensuite glisser la craie , le crayon en graphite ou encre le long de la règle.
B ) Par pliage : On trace deux points sur une feuille , on replie celle ci sur elle même autour des points A et B.
6°) Ci-dessous vous trouverez les « NOMS » de DROITES ou segment de droites particuliers donnés dans des constructions géométriques
	Hauteur
	Médiatrice
	Médiane
	Bissectrice
	Hypoténuse
	Apothème
	Diagonale
7°) Positions relatives d’une droite et d’un point.
Nous allons considérer une droite et un point : Deux cas peuvent alors se présenter
a) Le point se trouve sur la droite : Sur la figure ci contre : le point « C » est marqué sur la droite AB, il est un des points de cette droite. Sur une droite quelconque, il y a une infinité de points. (son nombre est infini.)
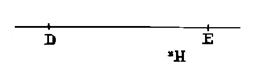
b) Le point ne se trouve pas sur la droite : Le point « H » n’est pas marqué sur la droite DE. (voir ci contre) ; on dit aussi que le point « H » est situé hors de la droite « DE » ou n’appartient pas à cette droite.
8°) Position relatives de deux droites . (info ++@ )
On comptera 3 cas .
a) Les deux droites données ont deux points communs ( ou plus de deux) alors elles coïncident ; ( on peut dire qu’elle fusionnent ou se superposent)
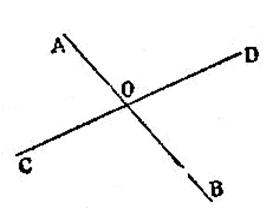
b) Les deux droites n’ont qu’un seul point commun , ainsi les deux droites « AB » et « CD » (figure ci contre) ont le point « O » commun et n’ont que celui là ; on dit « quelles se coupent » , « se rencontre » ou sont « concourantes » ou « sécantes » ; le point « O » est leur « point d’intersection », « leur point de rencontre » ou « leur point de concours ».
c) Elles n’ont aucun ( pas un seul ) point commun. Dans ce cas on dira qu’elles sont parallèles..
Revu le 4/01/2013

TRAVAUX AUTO FORMATIFS

CONTROLE :

1) Citer les deux propriétés de la droite ,et la propriété fondamentale de la droite.

2 ) Citer les trois sortes de droites.

3) Quel est l’outil que l’on utilise pour tracer une droite ? quelle précaution doit – on prendre ?

4 ) Citez l’axiome d’Euclide.

EVALUATION

Tracer une droite avec une règle.

(comment vérifier ! si elle est rectiligne )

@ INTERDISCIPLINARITE