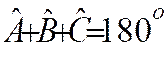Pré requis:
|
¥ |
|
|
¥ |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent 1°)Notions . 3°) Fiches de travail ( 4ème collège) |
Objectif suivant 1° ) Les droites caractéristiques dans un triangle rectangle |
|
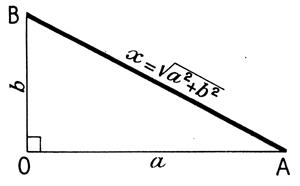
DOSSIER:LE TRIANGLE
RECTANGLE ABC.
|
|
- Rappels |
|
|
|
1°) Généralités. |
|
|
|
2°) Propriétés. |
|
|
|
|
|
|
|
|
|
|
|
Ü POSSIBILITES D ‘ IDENTIFICATION d ’UN TRIANGLE RECTANGLE |
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Liste des POSSIBILITES D ‘ IDENTIFICATION d
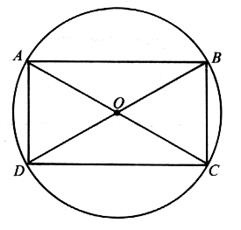
’UN TRIANGLE RECTANGLE . Définition : On appelle rectangle , un parallélogramme ayant un
angle droit . Propriétés : Nous admettrons qu'il en est ainsi , uniquement dans le cas où les diagonales [ AC ] et
[ DB] ont la même longueur . Il en résulte que dans un rectangle ABCD les quatre angles sont droits
:
Les côtés opposés sont
parallèles et ont la même longueur
: AB = CD et
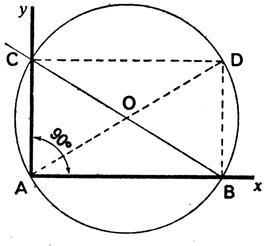
AD = BC Le point de concours des diagonales est équidistant des quatre sommets . Il existe donc
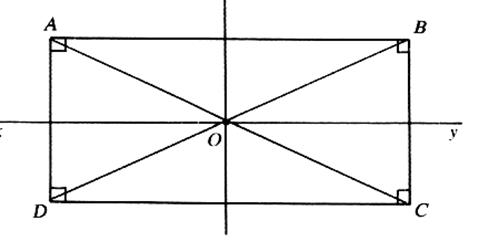
un cercle circonscrit au rectangle et son centre est le point de concours des diagonales . OA = OA = OC = OD . Le point "O" est centre de symétrie . Les droites x y et u v
, médiatrices des côtés opposés sont
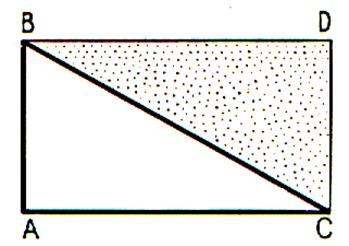
axes de symétrie . *Remarque : Soit le rectangle
BECA ; La figure BCA et la
figure BEC sont des demi - rectangles . On les appelle " triangle rectangle" , l'un est "rectangle" en
A , l'autre est "rectangle"
en E . ( les diagonales sont appelées :
"hypoténuse" )
|
|
||
|
|
|
|||
|
|
1°) Généralités. |
|
||
|
|
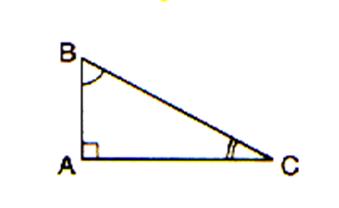
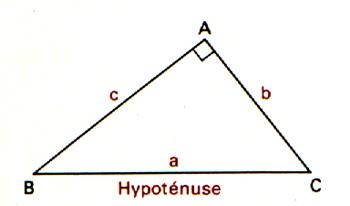
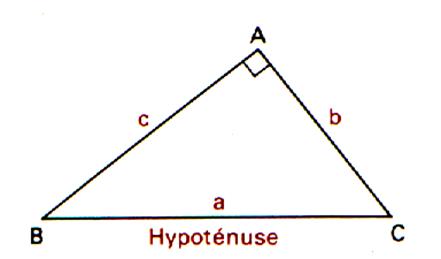
Un triangle rectangle est un polygone qui a trois côtés et trois angles ; dont un angle droit . Dans le
triangle ABC , les segments [BC] ; [AC] et [AB] sont
les côtés du triangle . |
|
|
|
|
|
|
|
||
|
|
On désigne souvent : Par " Par " Par " |
|
|
|
|
|
Nous désignons par |
|
||
|
|
Rappel 2 : Dans un triangle la
somme de ses angles est égale à 180° soit :
Rappel 3 : ANGLE : Un angle droit c’est : 90° = 100gr = Ce qui
est particulier au triangle rectangle :
Un triangle est rectangle si
deux de ses angles sont complémentaires. Rappel 4 : deux angles sont complémentaires @ si leur somme est égale à 90° : |
|
||
|
|
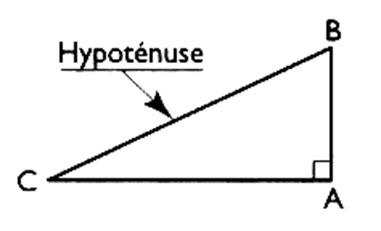
Les cotés formant les
angles complémentaires ,dans le triangle rectangle,
sont appelés : coté adjacent et
hypoténuse. |
|
||
|
|
|
|
|
|
|
|
2°) Propriétés : |
|
||
|
|
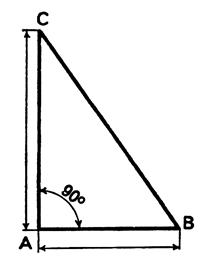
Considérons un triangle ABC , rectangle en
A , d'hypoténuse [ BC] . |
|
|
|
|
|
|
|
|
|
|
|
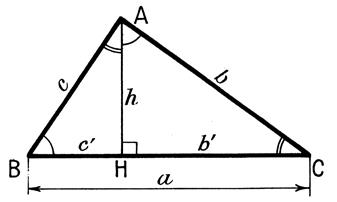
La hauteur issue du sommet B est la droite ( BA ) , la hauteur issue
du sommet C est
la droite ( CA) : l'orthocentre du
triangle ABC est le sommet
"A" . Désignons par "O" le milieu de
l'hypoténuse et soit "E" le symétrique de A par rapport à O . |
|
|
|
|
|
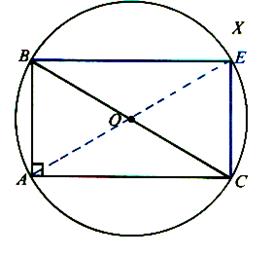
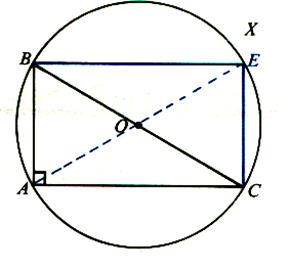
Le quadrilatère
BECA , ayant ses diagonales qui se coupent en
leur milieu , est un parallélogramme . Ce parallélogramme a un angle droit ,l'
angle "A" ,c'est donc un rectangle . Le point "O" qui est
le centre du cercle circonscrit au
rectangle BECA est donc le centre du
cercle circonscrit au triangle ABC . Nous retiendrons : Dans un triangle rectangle: -
le cercle
circonscrit admet l'hypoténuse pour diamètre
. -
La médiane relative à
l'hypoténuse est égale à la moitié de celle - ci . Remarque : la seconde partie de la propriété signifie que la
longueur du segment de médiane entre
le sommet de l'angle droit et l'hypoténuse est égale à la moitié de la
longueur de l'hypoténuse . |
|
||
|
|
|
Les dimensions : |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
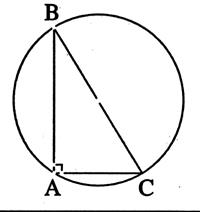
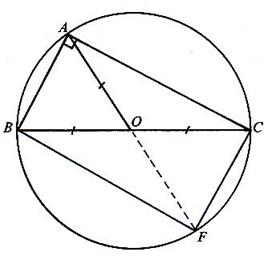
Considérons un triangle ABC où le milieu O de [BC] vérifie l'égalité :OA = OB = OC = ………….. mm. |
|
||
|
|
|
|
|
|
|
|
« O »
est donc le centre du cercle
circonscrit au triangle . Le symétrique
de "F" de A par rapport
à "O" appartient à ce
cercle . AF = BC . La quadrilatère
ACFB , ayant ses diagonales qui se coupent en
leur milieu , est un parallélogramme . Ce parallélogramme a ses diagonales de même longueur
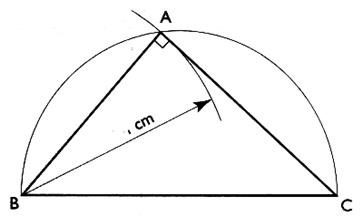
, c'est donc un rectangle et l'angle "A" est droit . Nous retiendrons la propriété suivante : Si dans un triangle , un
côté est diamètre du cercle circonscrit , alors ce triangle est rectangle et
admet le diamètre du cercle
circonscrit comme hypoténuse . Première
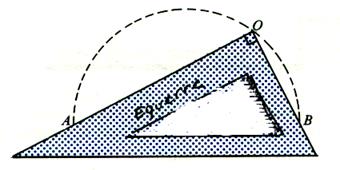
conséquence : Pour tout point M d'un demi- cercle de diamètre [AB] , on a Deuxième conséquence : On
peut tracer un demi - cercle de
diamètre [AB] avec une équerre . IL faut faire coïncider les deux côtés de l'angle droit avec A et B . La position du sommet O de l'équerre donne un point du
demi - cercle . On recommence en positionnant
l'équerre de façon différente . |
|
||
|
|
|
|||
|
|
Deux méthodes |
|
||
|
|
a) avec une équerre : |
|
||
|
|
On trace le segment AB ; on fait correspondre les points A
et B avec les bords de l'équerre . |
|
||
|
|
b ) Avec le compas et la
règle : |
|
||
|
|
Dont on connaît les dimensions :
Tracer l'hypoténuse BC (
segment [BC] ) ; puis avec un
compas tracer un arc BA ; puis pour situer le sommet A tracer l'arc AC ;
tracer ensuite les segments [AB] et [AC]. |
|
||
|
|
Ü POSSIBILITES D ‘ IDENTIFICATION d ’UN TRIANGLE RECTANGLE : Pour identifier un triangle rectangle , on peut : -
vérifier que ses
dimensions satisfont la
réciproque de la propriété de
Pythagore ; -
vérifier qu'il est inscrit
dans un demi - cercle dont le diamètre est l'hypoténuse du triangle . -
vérifier qu'un de ses angles
est droit à l'aide d'une équerre ou un
rapporteur . |
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
I ) Compléter les phrases suivantes : a)
Dans un triangle la somme de ses angles est égale
à ... Donner l’égalité mathématique : ................................
b )Par
définition : un triangle est rectangle si deux de ses angles sont.... c )
« deux angles sont complémentaires si leur somme est égale
à......... » Donner
l’égalité mathématique :........ 1°) Tracer un triangle
rectangle sans contrainte de mesure ( avec une équerre
et un compas ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|