Géométrie : DOSSIER : les tracés géométriques II / Objectif cours 24a

Pré requis:

Classes élémentaires ( primaire)
b) Tracé d’un triangle quelconque
c) Voir tracé du triangle équilatéral
d) Tracé du triangle isocèle
e) Tracé du triangle rectangle
Les triangles (caractéristiques )

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : Triangles caractéristiques 4^ème collège : Fiches sur : cercle , distance et inégalité….

Objectif suivant : Les triangles .

tableau Tout sur les informations triangles

DOSSIER : LES TRACES des TRIANGLES

Les constructions d’un triangle.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Travaux …les triangles et ……..

COURS

A ) TRACES

I ) Tracé d’un triangle dont on connaît deux cotés et l’angle compris entre deux cotés.
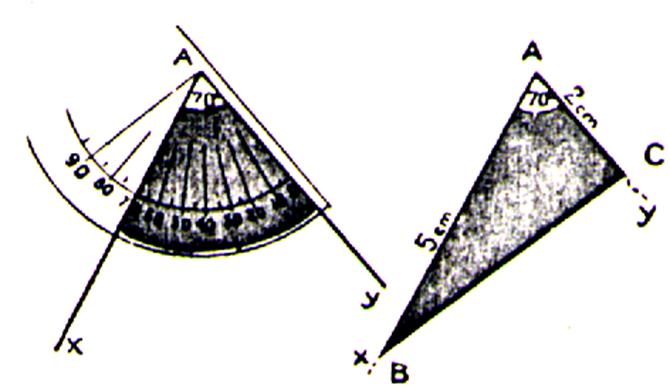
Exemple : tracer un triangle ABC dont AB = 5 cm ; BC = 2cm et l’angle A = 70 ° : Procédure : 1°) tracer l’angle xAy = 70° ; 2°)sur Ax porté « B » à 5 cm 3°)sur Ay porté « C » à 2 cm 4°) joindre les points B et C. le triangle ABC est tracé.

II ) Tracé un triangle dont on connaît un coté et les deux angles adjacents.
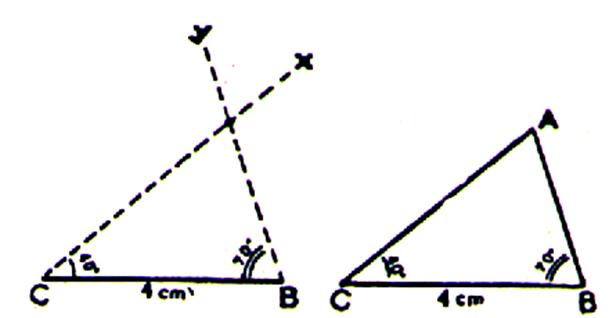
Exemple : tracer un triangle ABC avec BC = 4 cm , l’angle B = 70° et l’angle C = 40 °. Procédure : 1°) tracer le segment BC. 2°) tracer au rapporteur l’angle CBy =70° en B. 3°) tracer au rapporteur l’angle BCx = 40°. Les demi-droites By et Cx se coupent en un point A qui est le sommet du triangle.

III ) Tracé d’un triangle dont on connaît les trois côtés.

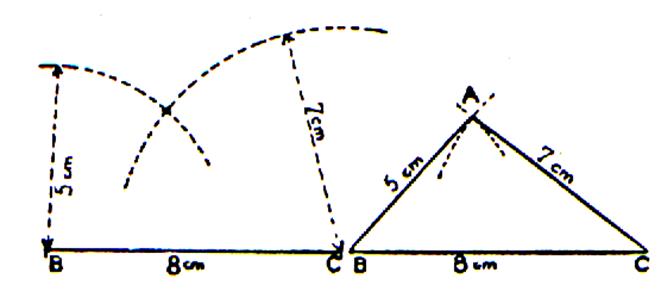
Exemple : tracé un triangle dont les cotés mesurent BC = 8 cm ; AB =5 cm et AC = 7cm. Procédure : 1°)tracer un segment de droite égale à celle d’un côté ,8 cm par exemple ;pour BC 2°)de « B » avec une ouverture de compas égale à BA = 5 cm ,tracer un arc de cercle . 3°) de « C » avec une ouverture de compas égale à CA = 7 cm ,tracer un arc de cercle . les deux arcs se coupent en « A » sommet du triangle .

2°) CONSTRUIRE par TRACE UN TRIANGLE QUELCONQUE

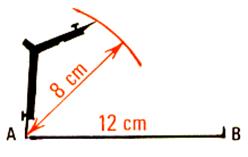
Exemple : tracer un triangle dont les côtés mesurent : AB = 12 cm ; AC = 8 cm ; BC = 10 cm

1°) Tracer le segment de droite AB

2°) régler l’écartement du compas ( règle graduée) à 8cm et tracé un arc de cercle

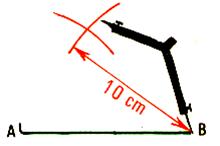
3°) régler l’écartement du compas ( règle graduée) à 10 cm et tracé un arc de cercle. Celui croise l’arc tracé précédemment.( point C)

4°) Tracer AC et BC

B ) TRACES PARTICULIERS

1°) CONSTRUIRE UN TRIANGLE EQUILATERAL ( Régulier)

Sur une feuille de papier tracer un triangle dont un côté mesure 6cm .avec le compas et la règle graduée.

Tracer un segment de 6 cm . Régler l’écartement du compas = 6 cm
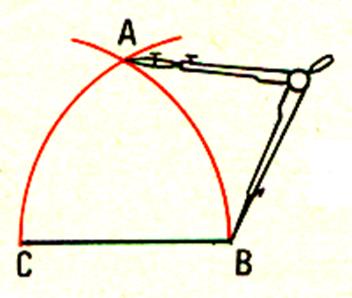
De C et B comme centre ; tracer deux arcs de cercle , se coupant en A
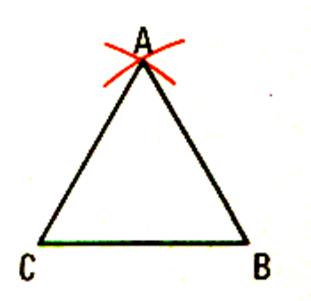
Tracer les segment CA et BA

2°)CONSTRUCTION DES TRIANGLES ISOCELES

Avec le compas et la règle : Un coté de 5cm les deux autres de 6cm
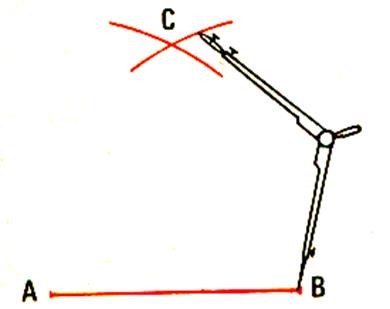
Tracer le segment AB ( = 5 cm ) Avec une ouverture de compas de 6 cm , tracer de A et de B comme centre deux arcs de cercle qui se coupent au point C . Joindre AC et BC

b) Avec l’équerre et la règle. : Un côté de 4cm et une hauteur de 7 cm
Tracer le segment AB = 4 cm Elever une perpendiculaire au milieu de AB . Sur cette perpendiculaire prendre un point C situé à 7 cm de AB. Joindre AC et BC

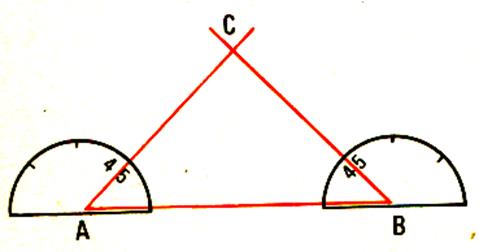
c) Avec le rapporteur . AB = 6 cm et deux angles = 45°
Tracer AB = 6cm Construire en A et en B un angle de 45°. Les côtés des deux angles se coupent au point C.

3°) Construire un triangle rectangle

- 3₁ avec l’équerre et la règle graduée

Construire un triangle rectangle dont les côtés de l’angle droit mesurent 8 cm et 6 cm .

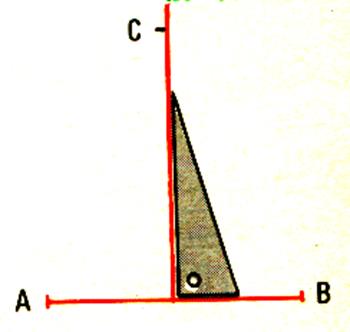
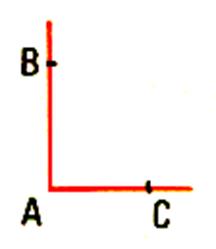
1°) Tracer un angle droit
2°) Porter sur les côtés de l’angle droit 2 segments AB = 8 cm AC = 6 cm
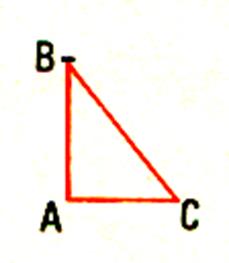
3°) Tracer le troisième côté .

- 3₂ Construire un triangle rectangle en partant d’un demi-cercle

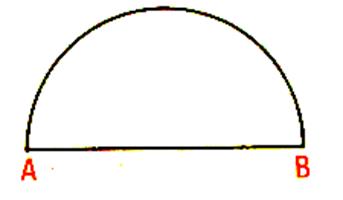
Tracer un demi – cercle
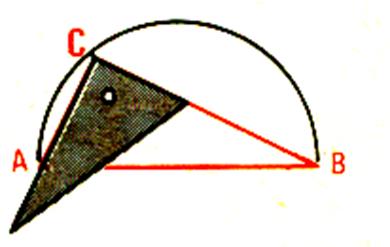
Placer un point « C » sur ce demi – cercle . Joignons C à A et à B Vérifier à l’équerre que nous avons tracé un triangle rectangle .

- 3₃ Tracer un triangle rectangle sans équerre , avec un compas.

Construire un triangle rectangle dont le grand côté mesure 10 cm et l’un des côtés de l’angle droit mesure 5 cm .

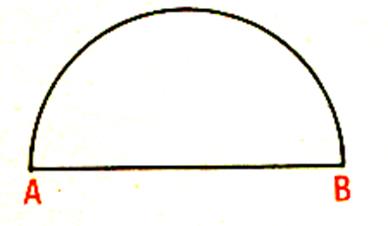
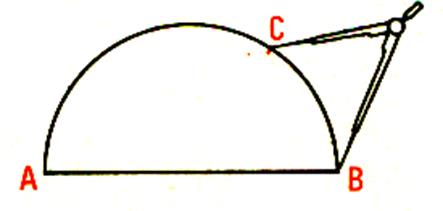
Tracer un demi – cercle de rayon : 5cm
Prendre un ouverture de compas de 5 cm, Marquer le point C . Tracer les deux segments AC et CB

TRAVAUX AUTO FORMATIFS.

CONTROLE:

I ) Donner la procédure permettant de Tracer un triangle dont on connaît deux cotés et l’angle compris entre deux cotés

2°) Donner la procédure permettant de Tracer un triangle dont on connaît un coté et les deux angles adjacents.

3°) Donner la procédure permettant de Tracer un triangle ABC dont on connaît les trois côtés.

EVALUATION:

1 °) tracer un triangle ABC dont AB = 5 cm ; BC = 2cm et l’angle A = 70 ° : (donner la procédure )

2°) tracer un triangle ABC avec BC = 4 cm , l’angle B = 70° et l’angle C = 40 °.(donner la procédure )

3° ) tracer un triangle dont les cotés mesurent BC = 8 cm ; AB =5 cm et AC = 7cm. (donner la procédure )

B ) TRACES PARTICULIERS

1°) CONSTRUIRE UN TRIANGLE EQUILATERAL ( Régulier)

Sur une feuille de papier tracer un triangle dont un côté mesure 6cm .avec le compas et la règle graduée.

2°)CONSTRUCTION DES TRIANGLES ISOCELES

a) Avec le compas et la règle

Un coté de 5cm les deux autres de 6cm

b)Avec l’équerre et la règle.

Un côté de 4cm et une hauteur de 7 cm

c) Avec le rapporteur .

AB = 6 cm et deux angles = 45°

3°) Construire un triangle rectangle

- 3₁ avec l’équerre et la règle graduée

Construire un triangle rectangle dont les côtés de l’angle droit mesurent 8 cm et 6 cm .

- 3₂ Construire un triangle rectangle en partant d’un demi-cercle

- 3₃ Tracer un triangle rectangle sans équerre , avec un compas.

Construire un triangle rectangle dont le grand côté mesure 10 cm et l’un des côtés de l’angle droit mesure 5 cm .

Autres travaux : tracer des 4 triangles ; et des droites et cercles inscrit et circonscrit.

Interdisciplinarité :

1°) tracer un triangle dont les cotés mesurent 3 cm ; 4 cm ; 5 cm

.Vérifier que c’est un triangle rectangle.

2°)Même tracer avec 33 mm ; 44 mm , 55 mm. Vous obtiendrez toujours un triangle rectangle .Vérifier que la somme des carrés des deux cotés de l’angle droit est égale au carré de l’hypoténuse.

Pour en savoir plus

Voir « Pythagore »

SUITE : CONSTRUIRE par TRACE UN TRIANGLE QUELCONQUE

Exemple : tracer un triangle dont les côtés mesurent : AB = 12 cm ; AC = 8 cm ; BC = 10 cm
1°) Tracer le segment de droite AB 2°) régler l’écartement du compas ( règle graduée) à 8cm et tracé un arc de cercle
3°) régler l’écartement du compas ( règle graduée) à 10 cm et tracé un arc de cercle. Celui croise l’arc tracé précédemment.( point C) 4°) Tracer AC et BC