Classe de 4^ème collège
			Liste des cours de 4^ème (programme)
	Corrigé (en cours )
Retour vers l’accueil « warmaths »			>> Liste des cours en géométrie ..
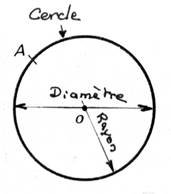
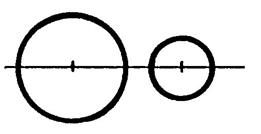
Ne pas confondre !!! « cercle » et « disque » ces deux mots désignent des « objets » différents.
CERCLE : une ligne particulière		DISQUE : une surface plane délimitée par une ligne particulière.

Pré requis:

Notions : plan –ligne – point
Matériel de traçage
Le nombre "pi"
La ligne courbe

ENVIRONNEMENT du dossier:

Index accueil warmaths

Objectif précédent 1°) Le cercle ( vu en primaire)

Objectif suivant : 1°)Les disques 2°) détermination du centre 3°) positions relatives de deux cercles 4°) positions relatives d’un cercle et d’une droite 5°) Cercle et symétrie. 6°) « Cercle » « disque » et « isométrie »

tableau 1°) Géométrie présentation 2°) Cours de niveau V 3°) Info complémentaires.

DOSSIER : LE CERCLE ; distance ; inégalité triangulaire.

Fiche 1 : Cercle.

Fiche 2 : Détermination d’un cercle.

Fiche 3 : Position relatives de deux cercles.

Fiche 3 bis.(positions relatives de deux cercles).

Fiche 4 : Construction de triangles.

Fiche 5 : Inégalité triangulaire

Fiche 6 : Régionnement du plan par la médiatrice d’un segment .

Fiche 7 : Distance d’un point à une droite.

Fiche 8 : Positions relatives d’une droite et d’un cercle.

Fiche 9 : Tangente à un cercle.

Fiche 10 : Propriété des points de la bissectrice d’un angle.

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Sciences	Corrigé Contrôle	Corrigé évaluation
				1°) Situation problèmes. 2°) Fiches module 5 : ……arithmétique. 3°) Fiche spécifique :…
Fiche : cercle et dessins.	Fiche : le cercle et le tracé	Fiche : cercle « exercices »	Fiche :cercle et problème.	Fiche : cercle et son périmètre.

Fiche 1 : Cercle.	Info ++@
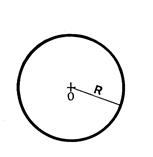
Définition : « O » étant un point du plan et « R » un nombre positif, on appelle « cercle » de centre « O » et de rayon « R » l’ensemble des points du plan …………………… ……………
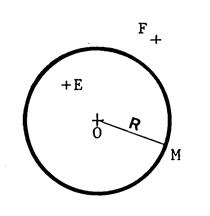
Etant donné un cercle de centre « O » et de rayon « R ». « M  est un point du cercle » signifie « OM = R ». « E est un point intérieur au cercle » signifie « OE …………….R ». « F est un point extérieur au cercle » signifie « OF …………………….. R ». Tout cercle admet un centre de symétrie qui est « ……. ». Tout cercle admet une infinité d’axes de symétrie ce sont ……………………………….
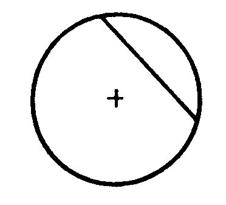
Corde :On appelle corde d’un cercle tout segment dont les extrémités sont sur le cercle. Démontrez oralement les théorèmes suivants : Théorème 12 : Dans tout cercle, la médiatrice de chaque corde passe par le ……………….. de ce cercle. Théorème 13 : Tout diamètre passant par le milieu d’une corde est …………….de cette corde. Théorème 14 :Tout diamètre perpendiculaire à une corde est ………….de cette corde.

Fiche 2 : Détermination d’un cercle.
1°) Cercles passant par un point. Ci-contre un point « P ». Activité : dessinez des cercles passant par « P ». Questions: Combien pouvez-vous en tracer ? ………….une infinité………. Quel est l’ensemble des centres de tels cercles ? ……………..
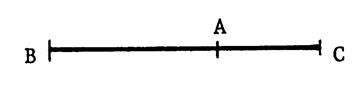
2°) Cercles passant par deux points distincts.
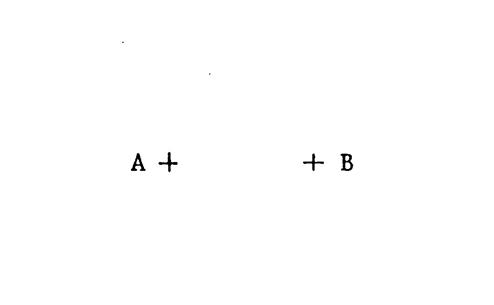
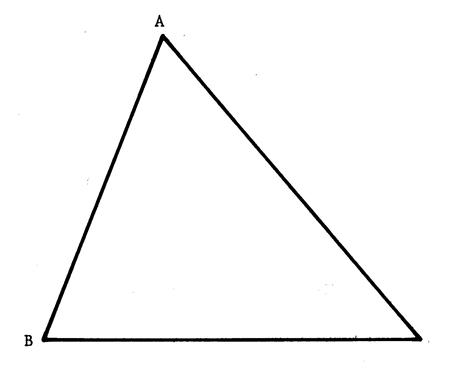
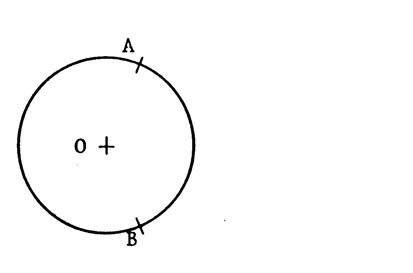
Ci-contre : Deux points « A » et « B ». Activité : Dessinez des cercles passant par « A » et « B ». « O » étant le centre d’un de ces cercles, puisque « A » et « B » sont des points de ces cercles alors «  OA … ..OB » . Donc , « O » est situé sur la ………………………de [AB]. Tracez cette droite sur la figure. § Choisissez un point « O’ » quelconque sur cette droite. § Dites en l’expliquant verbalement si ce point peut être considéré comme le centre d’un cercle passant par « A » et « B ». On peut alors dire :
Théorème 15 : Par deux points « A » et « B » , il passe une infinité de cercles. L’ensemble des centres de ces cercles est la ………………………………… de [AB].
3°) Cercle passant par trois points distincts.
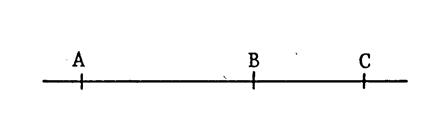
On donne trois points distincts « A », « B » et « C ». On se propose de déterminer un ( ou des ) cercle (s) passant par « A », « B » et « C ». Soit « O » le centre d’un tel cercle ( s’il existe ) . Ce cercle devant passer par « A », « B » , « O » doit être situé sur la médiatrice de …………. Ce cercle devant passer par « B », « C » , « O » doit être situé sur …………………………………………… ; …………. « O » est alors situé à l’intersection ( si elle existe ) de ces deux droites.
v Les trois points « A », « B » et « C » sont alignés. Tracez les médiatrices de [AB] et de [BC]. Que constatez-vous ?
Démontrez le. Ces droites ont- elles un point commun ? …………………………………………………………………………….. Donc « O » existe-t-il ? ……………………………………………………………………………
Théorème 16. Il n’existe pas de cercle passant par 3 points distincts alignés.
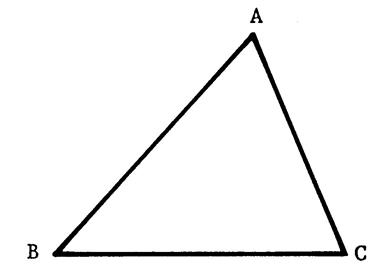
v Les trois points « A », « B » et « C » ne sont pas alignés. Tracez les médiatrices de [AB] et de [BC]. Les droites ( AB ) et ( BC ) n’ayant pas la même direction, les médiatrices se coupent. Soit « O » le point d’intersection. Il est unique. « O » étant sur la médiatrice de [AB] alors «  OA OB » . « O » étant sur la médiatrice de [……] alors «  …………… » . Par transitivité de l’égalité , on a «  OA = ……….= ……… » Le cercle de centre « O » passant par « A » passe donc aussi par ….et par …….. Ce cercle est unique, tracez- le.
Théorème 17. ¨Par trois points non alignés , il passe un cercle et un seul.
Remarque 1 : Si deux cercles ont en commun au moins 3 points , ces cercles sont ………………………………………………………… Remarque 2 : Deux cercles distincts ne peuvent donc pas avoir plus de ……………………………..points communs.

Fiche 3 : Position relatives de deux cercles.		Info +++@ ….
Activité : on vous demande de remplir la fiche suivante « Fiche 3 bis ». Pour ce faire : On considère deux cercles , l’un de centre « O » et de rayon « R », l’autre de centre « O’ » et de rayon « R’ » tel que «  R R’ ». On appelle « d » la distance de leurs centre . « OO’ = d ». Suivant la valeur de cette distance , les cercles occupent diverses positions l’un par rapport à l’autre. Voici , ci –dessous, toutes les situations possibles , dans un ordre quelconque.
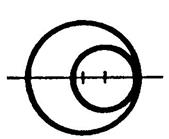
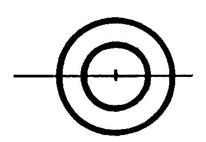
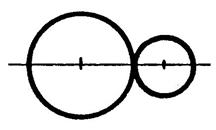
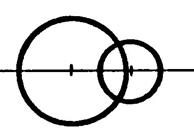
Position 1	Position 2		Position 3
Position 4	Position 5		Position 6
Complétez le tableau représentant dans chaque case le dessin correspondant convenablement choisi parmi l’un des six ci-dessus. ( Placez le centre des cercles ). Vous prendrez pour rayon R = 19 mm et R’ = 13 mm . Dans chacun des cas , vous préciserez la distance de « d » (en mm) que vous aurez choisie. Vous indiquerez le nombre de points d’intersection des deux cercles.

Fiche 3 bis.(positions relatives de deux cercles).
Relation entre la distance « d » et les rayons.	Désignation et nombre de points communs.	Dessin.
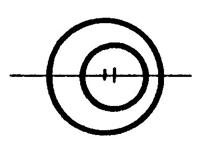
« d = 0 »	Cercles concentriques. ……….point commun	« d = ……… »
«  d < R – R’ »	Un cercle est à l’intérieur de l’autre. ……….point commun	« d = ……… »
« d = R – R’ »	Cercles tangents intérieurement. …. Point commun situé sur « OO’ »	« d = ……… »
R-R’ < d < R+R ’	Cercles sécants . ………points communs	« d = ……… »
d < R + R’	Cercles tangents extérieurement. ….point commun situé sur « OO’ »	« d = ……… »
d > R + R’	Cercles extérieurs. …..point commun	« d = ……… »

Fiche 4 : Construction de triangles.		Info +++ @ triangle tracé…
Dans les trois cas suivants vous allez construire, si cela est possible, un triangle dont les mesures des côtés sont les nombres donnés . ( ce sont des millimètres) . Pour faire ces constructions , il vous faudra tracer des cercles. Précisez dans chacun des cas la position relative de ces cercles. ( voir la fiche 3 ) et écrivez, avec les nombres donnés , l’égalité ou les inégalités correspondantes.
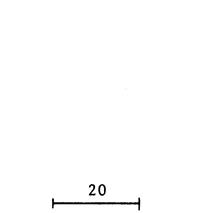
1^er cas : mesure de côtés : 50 mm , 40 mm, 30 mm. Faîtes trois dessins en partant chaque fois du côté déjà placé.
Dessin1	Dessin 2		Dessin 3
Position des cercles : …………………………	Position des cercles : …………………………		Position des cercles : …………………………
Egalité ou inégalités : …………………………	Egalité ou inégalités : …………………………		Egalité ou inégalités : …………………………
Tous les triangles obtenus sont-ils superposables ?........
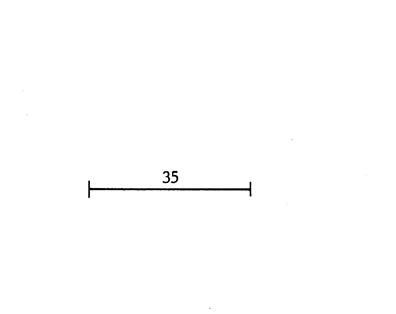
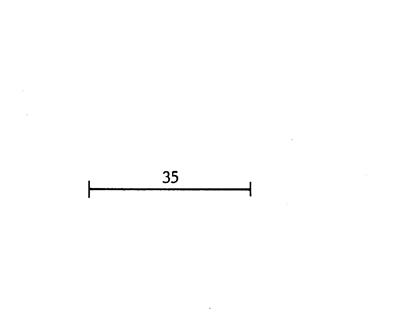
2^ème cas : mesure de côtés : 35 mm , 17 mm, 13 mm. Faîtes deux dessins en partant chaque fois du côté déjà placé.
Dessin1		Dessin 2
Position des cercles : …………………………		Position des cercles : …………………………
Egalité ou inégalités : …………………………		Egalité ou inégalités : …………………………
Le triangle existe-t-il ? …………………………………………………………………………
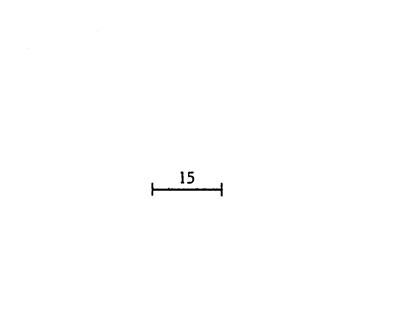
3^ème cas : mesure de côtés : 35 mm , 20 mm, 15 mm. Faîtes deux dessins en partant chaque fois du côté déjà placé.
Dessin1		Dessin 2
Position des cercles : …………………………		Position des cercles : …………………………
Egalité ou inégalités : …………………………		Egalité ou inégalités : …………………………
Le triangle existe-t-il ? …………………………………………………………………………

Fiche 5 : Inégalité triangulaire	Info + @ inégalité triangulaire.
Dans la fiche 4 , vous avez pu constater qu'il n'est pas toujours possible de dessiner un triangle dont les mesures des côtés sont trois nombres donnés quelconques.
· Le triangle est « aplati » dans le cas où les cercles sont …………………... Dans ce cas, un des nombres est égal à la ………………. des deux autres ou ce qui revient au même, un des nombres est égal à la ……des deux autres. · Le triangle n'existe pas dans le cas où les cercles ne se …………………… Dans ce cas, un des nombres est strictement ……………….. à la somme des deux autres ou ce qui revient au même, un des nombres est strictement ………………………. à la différence des deux autres.
· Le triangle existe uniquement dans le cas où les cercles se ..….. Dans ce cas, chacun des nombres est strictement ………………………. à la somme des 2 autres et chacun des nombres est strictement …………………….à la différence des deux autres.
Remarque 1 On peut dire que le triangle existe uniquement dans le cas où le « plus grand côté » est inférieur à la somme des deux autres (explique oralement pourquoi les autres conditions sont automatiquement vérifiées).
Conséquences : Etant donnés 3 points « A »,  « B » , « C » distincts si ces points ne sont pas alignés, ils déterminent un triangle. Puisque ce triangle existe c'est donc qu'un côté quelconque est strictement inférieur à la somme des deux autres. On peut donc écrire : BC BA + AC.
Si les trois points sont alignés le triangle est aplati. Un des points est situé sur le segment déterminé par les deux autres. En appelant « A » ce point, on a alors BC BA + AC. et par conséquent BA BC + AC et AC BC + BA.
II n'y a pas de cas où l'on puisse écrire BC > BA + AC. En définitive on peut dire :
Propriété 39 : A , B , C étant 3 points quelconques du plan, alors BC BA + AC BC = BA + AC signifie que A est situé sur [ bc] .
Remarque 2 L'inégalité ci-dessus est connue sous le nom d'inégalité triangulaire.
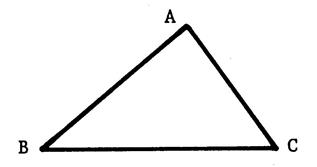
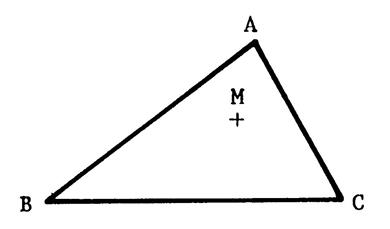
Exercice : « ABC » est un triangle quelconque et « M » un point " à l'intérieur" du triangle « ABC ». Nous allons démontrer que le trajet (B,M,C) est plus court que le trajet (B,A,C). C'est-à-dire que BM + MC < BA + AC. Activité : Tracez (BM) qui coupe (AC) en « E » et tracez [MC]. Dans le triangle « MEC », grâce à la propriété 39, on peut écrire : MC < ME + ……….
Ajoutons BM aux deux membres de cette inégalité (cours sur … Fiche 5) : BM + MC < BM + …..+ ……. « M » est un point à l'intérieur du triangle , donc « M » est situé sur [BE], donc BM + ME = ………. L'inégalité précédente s'écrit alors : BM + MC < …… + …….. ( 1)
Dans le triangle « BAE », grâce à la propriété 39, on peut écrire : BE < B A + ……… Ajoutons « EC » aux deux membres de cette inégalité, on obtient : BE + EC < BA + ……+ ………. Or, « E » est un point de [AC] , donc AE + EC = ………….. L'inégalité précédente s'écrit alors : BE + EC < BA +…………… (2) En considérant les inégalités (1 ) et ( 2 ) , on peut écrire : ………+………. < ………+ ……….

Fiche 6 : Régionnement du plan par la médiatrice d’un segment .				Info @ ……
Problème : Etant donné deux points distincts A et B, cherchons où se situent les points M du plan tels que MA < MB ou MA > MB .
Vous connaissez , déjà l'ensemble des points « M » tels que « MA = MB ». Cet ensemble est constitué par les points de la …………………. De [ AB ]
Tracez cette droite sur la figure ci-contre. Appelons-la « d ». Cette droite partage le plan en deux demi-plans, l'un contenant « A » , l'autre contenant « B ». Elle coupe [AB] en son milieu. Appelons-le « O ». Pour tout point « M » situé sur la demi-droite [OA, on a évidemment MA …….. MB.
Choisissez un point « M » dans le demi-plan contenant « A », « M » non situé sur [OA ni sur « d » . Tracez [MA] et [MB] . « M » et « B » étant de part et d'autre de « d », la droite d coupe [MB] en un point « E » situé entre « M » et « B » donc MB = ME + EB
Tracez [EA] et appliquons la « propriété 39 » au triangle « MAE » : MA < ……….. + ………….. Or « E » est un point de la médiatrice de [AB] donc EA = ……………………………. En remplaçant « EA » par « EB » dans l'inégalité précédente, on obtient : MA <………..+ …………. et comme ME + EB = …………. alors MA <………………… II en est ainsi pour tout point « M » situé dans le demi-plan contenant « A » ( « d » exclue). On prouverait de même que : MA > MB pour tout point M situé dans le demi-plan contenant ……………… ( « d » exclue ). On énoncera alors :
Théorème 18 : Etant donné, deux points « A » et « B » , en appelant « d » la . Médiatrice de [ab] , L’ensemble des points « M » du plan tels que MA = MB est la médiatrice de. [ab], L’ensemble des points « M » du plan tels que MA MB est le demi-plan de frontière « d » contenant « A » ( « d » exclue) L’ensemble des points « M » du plan tels que MA MB est le demi-plan de frontière « d » contenant « B » ( « d » exclue)
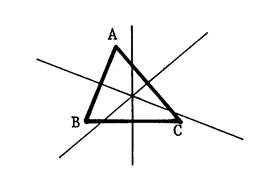
Exercice On donne 3 points « A » , « B » , « C ». Tracez les médiatrices de [AB] , [BC] , [ÇA] . (comme sur la figure ci-contre) (remarque : MA< MB < MC )
Vous savez que les médiatrices d'un triangle sont concourantes. Ces trois droites déterminent donc entre elles ………. zones dans le plan. « M » étant un point quelconque d'une des zones, vous allez écrire une double inégalité entre MA , MB , MC.
Exemple : Pour la zone contenant le point A, par rapport à la médiatrice de [AB], on peut écrire MA< MB, par rapport à la médiatrice de [AC], on peut écrire MA<C.MC, par rapport à la médiatrice de [BC], on peut écrire MB<CMC, On en déduit que MA < MB < MC. Activité : Faites de même pour les autres zones, (écris la double inégalité dans la zone correspondante).

Fiche 7 : Distance d’un point à une droite.			Info +++@ +++++
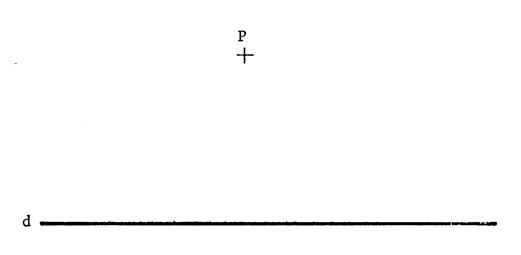
Voici , ci-contre , une droite « d » et un point « P ». Choisissez quelques points de « d » et mesurez leur distance à « P ». Vous constatez que ces distances sont différentes d'un point à l'autre. On se propose de chercher un point de « d » pour lequel la distance à « P » soit la plus petite possible. Q’ avez- vous trouvé ?...................................................
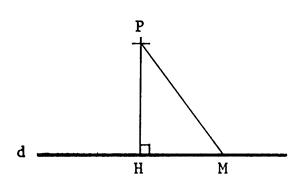
Voici comment on peut le démontrer : Appelons « H » le projeté orthogonal de « P » sur « d ». Appelons « M » un point quelconque de « d », « M H ». Le triangle « PHM » est rectangle en « H ». Or, vous savez (théorème 11) que dans tout triangle rectangle l'hypoténuse est le plus ………… des côtés. Donc PM………..PH. Donc « H » est le point dont la distance à « P » est la plus ………………..
Définition : On appelle distance d'un point à une droite , la distance, du point à son projeté orthogonal sur cette droite.
ENSEMBLE DES POINTS SITUÉS A UNE DISTANCE IMPOSÉE D'UNE DROITE DONNÉE
Ci –contre : On donne une droite «  » . Activité : Placez des points dont la distance à «  » (en mm) est 12. Activité : Tracez en rouge l'ensemble de tous les points possibles. Puis démontrez (oralement) le théorème :
Théorème 19 : L’ensemble des points situés à une distance imposée d’une droite donnée est constitué par ………………………………………………………..
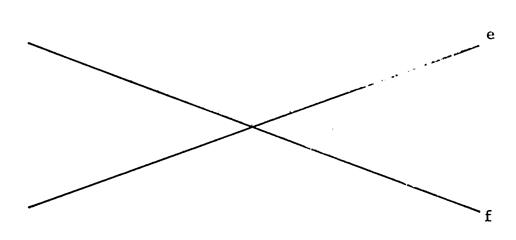
Exercice 1 : Ci-contre. Voici deux droites « e » et « f » . Déterminez les points qui sont à la fois à 10 mm de « e » et à 8mm de « f ».
DISTANCE DE DEUX PARALLELES.
Vous avez vu en 5^ème collège que :
Définition On appelle « distance de deux parallèles , la distance d’un point de l’une à son projeté orthogonale sur l’autre.
Exercice 2 Dans un parallélogramme, on appelle " hauteur " la distance des côtés opposés parallèles. Mesurez les hauteurs du parallélogramme ci-contre. Vous trouvez :……………..mm et …………..mm.

Fiche 8 : Positions relatives d’une droite et d’un cercle.		Info + @+++
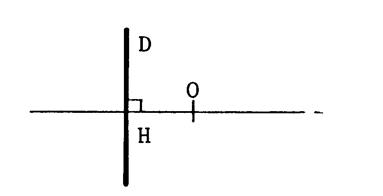
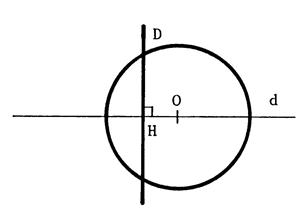
ci-contre , voici une droite « d » et une droite « D » perpendiculaire à « d », coupant « d » en « H ». Considérons des cercles dont le centre « O » est sur « d ». La distance de « O » à « D » est égale à « OH ».
1^er Cas « H »  EST EXTERIEUR AU CERCLE C'est-à-dire OH ……R Pour tout point M de D, OM OH (théorème ) Donc, par transitivité OM…….R Donc , la droite et le cercle ont ……….  point commun. On dit alors que la droite est extérieure au cercle.
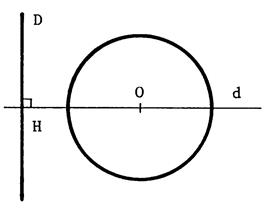
2^ème Cas « H » EST SUR LE CERCLE C'est-à-dire « OH ….R » On démontre comme précédemment que : Pour tout point « M » de « D » autre que « H », « OM……..R » Donc, la droite et le cercle ont ………….point commun.
Définition On appelle « tangente » , à un cercle toute droite qui n'a qu'un point commun avec le cercle.	Théorème 20 Toute, droite passant par un point d'un cercle et perpendiculaire au rayon passant par ce point est tangente à ce cercle.
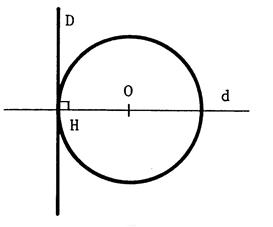
3^ème Cas : « H » EST INTERIEUR AU CERCLE C'est-à-dire OH…….R. Il est possible de démontrer que la droite et le cercle ont ……….points communs. On dit que la droite est sécante au cercle.
Remarque Grâce au « théorème 16 », on peut dire : Une droite et un cercle ne peuvent pas avoir plus de deux points communs.
RECIPROQUES 1°) Si la droite est extérieure au cercle, peut-on avoir OH = R ?........ OH<R ?................... (Explique pourquoi oralement). Donc il reste OH ……..R. 2°) Si la droite est tangente au cercle, peut-on avoir OH < R ?......... OH>R ? ……………… (Explique pourquoi oralement). Donc il reste OH……..R. 3°) Si la droite est sécante au cercle, peut-on avoir OH > R ? OH = R ? (Explique pourquoi oralement). Donc il reste OH ……..R.
Théorème 21 : 1°) Une droite est extérieure à un cercle si et seulement si sa distance au centre est strictement supérieure au rayon. La droite et le cercle ont alors 0…. point commun. 2°) Une droite est tangente à un cercle si et seulement si sa distance au centre est égale au rayon. La droite et le cercle ont alors …1 ... point commun. 3°) Une droite est sécante à un cercle si et seulement si sa distance au centre est strictement inférieure au rayon. La droite et le cercle ont alors 2…. point commun.
Dans le cas d'une droite tangente à un cercle, on peut transcrire le théorème de la manière suivante
Théorème 22 Toute tangente à un cercle est perpendiculaire. au rayon passant par le point commun au cercle et à cette droite.

Fiche 9 : Tangente à un cercle.	Info +++@ tangentes au cercle …..
Voici un cercle de centre « O » et 2 points « A » et « B » de ce cercle non diamétralement opposés.
Tracez par « A » et par « B » les tangentes à ce cercle. (pensez au théorème 22) . Puisque « O » ,  « A » ,  « B » ne sont pas alignés, les tangentes se coupent (expliquez). Appelons « P » le point d'intersection.
1°) Démontrez que « O » , « A », « P », « B » sont situés sur un même cercle dont vous préciserez le centre.
2°) a) Tracez le cercle de diamètre [OP]. b) Démontrez que la figure admet un axe de symétrie. c) Démontrez que [OP est la bissectrice de et [PO bissectrice de et que PA = PB.
3°) Sachant que le rayon du cercle est 15cm et OP = 39cm , calculez PA et PB et une valeur approchée à 1° près de .
Construction des tangentes à un cercle passant par un point extérieur au cercle.
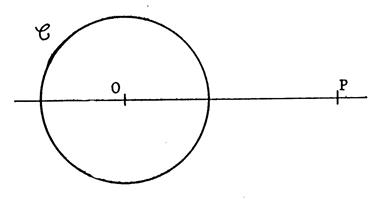
On donne un cercle « C » de centre 0 et un point P extérieur au cercle. On demande de construire les droites passant par P et tangentes au cercle « C » .
La figure de l'activité précédente vous suggère de tracer le cercle de diamètre []OP] . Ce cercle coupe le cercle £ en 2 points A et B. Grâce au théorème 8, puisque [OP] est diamètre, alors (PA) est perpendiculaire à (OA) et comme [ÔA] est rayon du cercle « C » , alors grâce au théorème 20, (PA) est tangente au cercle. Il en est de même pour (PB). Complétez la figure.
Activité : On donne un cercle de centre 0. [AB] est un diamètre du cercle. « M » est un point quelconque du cercle, M A , M B. 1°) Tracez les droites « d » et « d’ » respectivement tangentes en « A » et  « B » au cercle. Démontrez que « d » et « d »' sont parallèles. 2°) Tracez «   »   tangente en « M » au cercle. «   »   coupe « d » en « E » et «d' » en « F ». Trace [OE et [OF. Démontrez que  est droit. (Utilisez le « 2° » de l'activité du début de la fiche ). 3°) Démontrez que OE 0F = OM EF. (Utilisez le calcul d'aire). 4°) Démontrez que l'aire du trapèze « AEFB » est le double de l'aire du triangle « OEF ». Déduisez -en que « AE + BF = EF » 5°) Démontrez d'une autre façon que « AE + BF = EF » (Utilisez le 2° du début de la fiche ). ,

Fiche 10 : Propriété des points de la bissectrice d’un angle.		Info +++@ tangentes et bissectrices …..
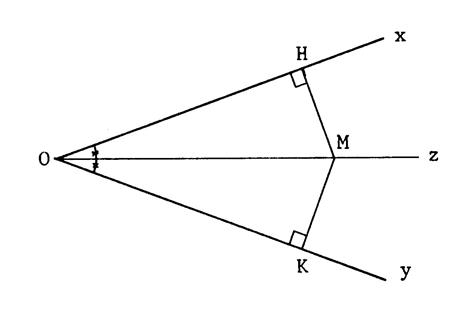
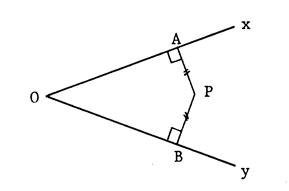
Voici, ci-contre , un angle et sa bissectrice [Oz. « M » est un point quelconque de [ Oz. « H » est le projeté orthogonal de « M » sur [Ox. « K » est le projeté orthogonal de M sur [Oy. Appelons «   »    le support de [Oz. «   »    est axe de symétrie de . Expliquez pourquoi (oralement) « H » et « K » sont symétriques par rapport à «   »   .
On en déduit alors que MH ………..MK. Donc M est ……………………………………. de [ Ox et de [Oy.
Théorème 23 Tout point de la bissectrice d'un angle est équidistant des côtés de cet angle.
Réciproque « P » est un point à l'intérieur de l'angle . « A » est le projeté orthogonal de « P » sur le support de [Ox. « B » est le projeté orthogonal de « P » sur le support de [Oy. « P » est tel que « PA = PB ».
Démontrons que « P » est sur la bissectrice de . Les triangles « OPA » et « OPB » sont des triangles rectangles. Grâce au théorème de Pythagore, on peut écrire : OA² = OP² - PA² et OB² =……… ……….. Puisque par hypothèse « PA = PB » alors « OA² = OB² » et par suite « OA = OB » . Sachant que « PA = PB » et « OA = OB » on en déduit que (OP) est ………………………………. de [AB ]. (OP) est donc « axe de symétrie » de la figure donc [OP est …………………………...
Théorème 24 Tout point équidistant des côté d'un angle est situé sur la bissectrice de l'angle.
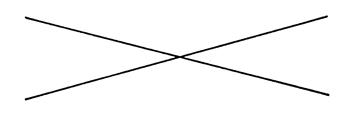
Exercice 1 Tracez l'ensemble des points équidistants des deux droites sécantes ci-contre. Cet ensemble est constitué par deux droites. Ces deux droites sont …………………………………………………. Expliquez pourquoi (oralement).
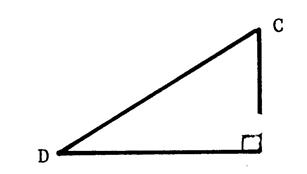
Exercice 2. « CED » est un triangle rectangle en « E ». La bissectrice de coupe (ED) en « F ». Démontrez que EF < FD. (Utilisez le projeté « G » de « F » sur (CD)).
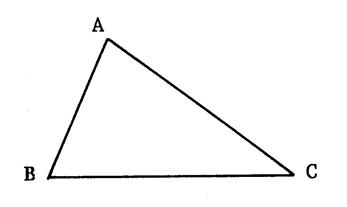
Exercice 3 « ABC » est un triangle quelconque. La bissectrice de et la médiatrice de [BC] se coupent en « M ». « H » et « K » sont les projetés orthogonaux de « M » sur (AB) et sur (AC). Démontrez que « HB = KG » » (Utilisez le théorème de Pythagore).
Exercice_4 On donne un segment [AB ] et deux demi-droites parallèles [Ax et [By situées dans un même demi-plan de frontière (AB). Les bissectrices de et se coupent en « C ». « C » se projette en « E » sur [Ax , en « F » sur [By et en « H » sur (AB). 1°) Démontrez que « C » est le milieu de [EF] (Utilisez CH). 2°) Démontrez que le cercle passant par « E »,  « H » , « F » est tangent à (AB). 3°) Démontrez que le triangle « EHF » est rectangle en « H ».
29/11/2014

TRAVAUX AUTO – FORMATIFS.

CONTROLE :

I ) Donner les définitions des caractéristiques suivantes :

centre 

cercle

Rayon 

diamètre

circonférence

disque

arc de circonférence

corde

Angle au centre

II) Quelles sont les positions d’un point par rapport à un cercle. ?

III) Quelles sont les positions d’une droite par rapport à un cercle ?.

IV) Quand dit - on que droite est tangente à un cercle ?

EVALUATION :

1°)Tracer un cercle et tracer et nommer la flèche ; la corde , le diamètre , le centre, le rayon , une tangente et une sécante

2°) D’un point situé à 12 cm du centre d’un cercle de 6cm de rayon , on mène deux tangentes à ce cercle. Quel est leur angle ?

3°) devoir de tracés : cliquez ici

( à imprimer )