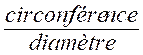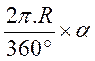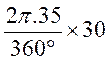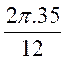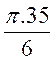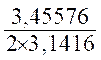Pré requis:
|
Les
conversions de longueurs |
|
|
Périmètre
(définition) |
|
|
Rappels
géométriques |
|
|
Tracés
géométriques (angles) |
|
|
« pi » |
|
|
Les unités
de longueurs |
|
|
|
ENVIRONNEMENT du dossier:
|
|
||||||||||||
|
|
||||||||||||
|
|
DOSSIER
« géométrie » : Calcul de
la longueur de la circonférence du cercle |
|
||||||||||
|
|
1°) Calcul de la LONGUEUR de la circonférence
du cercle |
|
||||||||||
|
|
2°) Calcul de la Longueur d’un arc de cercle |
|
||||||||||
|
|
3°) Applications aux cas courants. |
|
||||||||||
|
|
Recherche par le CALCUL DU
DIAMETRE et DU RAYON |
|
||||||||||
|
|
|
|
||||||||||
|
|
Problème
de niveau I : Stade : « des tours de piste »: Calculs
numériques |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
TEST |
COURS |
|
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
Info : Problèmes suite. La longueur est une « GRANDEUR » ; GRANDEUR: Une grandeur est un nombre
associé à une unité. |
|
|
|
|
|
|
|
|
|
|
|
1°)
Calcul de la LONGUEUR de la
circonférence du cercle :
( se rappeler que p = |
|
|
|
On
obtient la longueur de la
circonférence en multipliant le
diamètre par 3,1416 |
|
|
|
En
effet puisque p
=
|
|
|
|
La
longueur de la circonférence du cercle est égale au périmètre du disque "Pd".
Pd = p D ou sachant que D (Diamètre du cercle = 2 fois le rayon
"R") on peut aussi écrire
que Pd = 2pR |
|
|
|
La
longueur de la circonférence du cercle est égale au périmètre du disque "Pd".
Pd = p D ou sachant que D (Diamètre du cercle = 2 fois le rayon
"R") on peut aussi écrire
que Pd = 2pR |
|
|
|
Application :
Trouver la
circonférence d’une roue de 0,30 m de
rayon. On sait que : Pd =2r
|
|
|
|
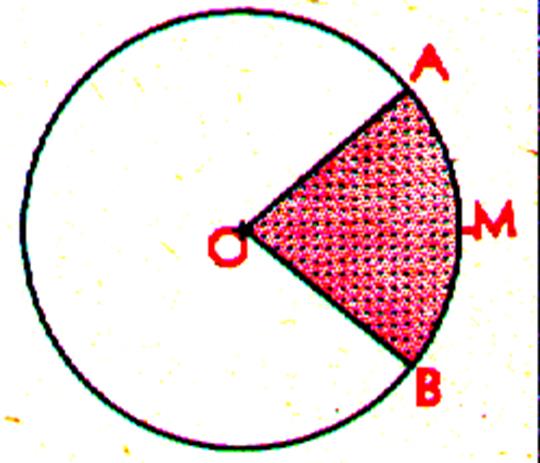
2°) Calcul de la longueur d’un arc. |
|
|
|
On obtient la longueur d’un arc
en multipliant la longueur de la circonférence par le nombre de degrés de
l’arc et en divisant le produit par 360. |
|
|
|
Calcul de
la longueur d’un arc de cercle dont l’angle est exprimé en degrés : |
|
|
|
Formule : lg arc = |
|
|
|
On divise
le périmètre du cercle en 360 parties égales ; pour multiplier par le
nombre degrés de l’angle
au centre de l’arc. |
|
|
|
|
|
|
|
Si l’angle alpha(
On sait que lg arc = soit : lg arc = |
|
|
|
En statistique une des
représentations graphiques des pourcentages est le « diagramme
circulaire » .
La circonférence est divisée en 100 parties égales ; Relation entre % et valeur en
degré : 360° représente
100% ; soit Le
1% représente 3,6° d’angle |
|
|
|
|
|
|
|
|
|
|
|
3°) Applications aux cas courants. |
|
|
|
Exercices : |
|
|
|
1 ) Calculer la longueur du périmètre du
disque de 10 cm de rayon. |
|
|
|
Corrigé : a )inventaire
de ce que je connais : Pd = 3,14 b) On remplace dans
Pd la valeur de R : Pd
= 3,14 c) Calcul : 3,14 d) Conclusion : la longueur du périmètre du disque est de
628 cm |
|
|
|
2 )Calculer la longueur du périmètre du disque de 10cm de diamètre. |
|
|
|
Corrigé : a )inventaire
de ce que je connais : Pd = 3,14 b) On remplace dans
Pd la valeur de D : Pd
= 3,14 c) Calcul : 3,14 d) Conclusion : la longueur du périmètre du disque est de
314 cm |
|
|
|
|
|
|
|
Recherche par le CALCUL DU
DIAMETRE et DU RAYON |
|
|
|
On obtient : Le DIAMETRE en divisant la longueur de la
circonférence par 3,1416 Et le RAYON , en divisant
la longueur de la circonférence par 2p En effet : Pd =
p D ou
Pd = 2pr Donc D = Application : Trouver le rayon d’un cerceau de
3,45576 m de longueur. r = |
|
|
|
Compléter le tableau suivant : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cercle
1 |
Cercle
2 |
Cercle
3 |
Cercle
4 |
|
P ou Lg Arc
|
|
628
cm |
628
mm |
|
|
R |
15
dm |
|
|
20
m |
|
D |
|
|
|
|
|
Angle
au centre |
360° |
360° |
90° |
38° |
|
|
TRAVAUX AUTO – FORMATIFS : |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
1
°) Donnez la définition de
"périmètre" 2° ) Quelle est l'unité usitée pour exprimer le résultat du
calcul du périmètre ? 3° ) Donner la définition littérale relatif au calcul du périmètre du cercle 4° ) Donner la formule permettant de calculer la
longueur d' un arc de cercle d'angle "alpha" Exercices :
compléter le tableau suivant
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
INTERDISCIPLINARITE
PROBLEMES : Série 1
. Série 2
Série 3
Problème
de niveau I « des tours de
piste »:
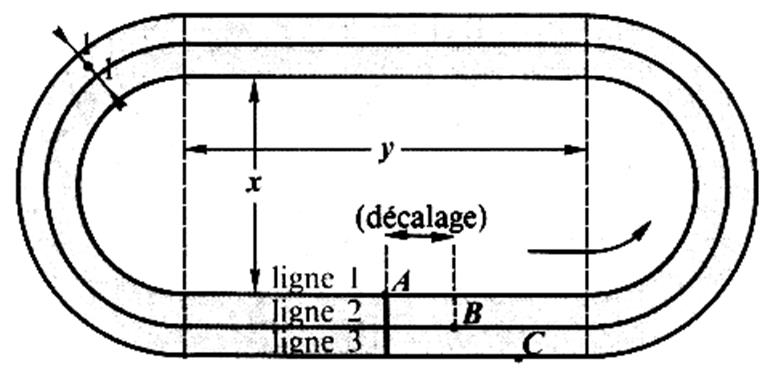
Calculs numériques Une piste
d'athlétisme possède 4 couloirs , un couloir par coureur. Dans le
dessin ci- dessus les couloirs ne sont pas dessinés ,les
lignes représentent le milieu ( l'axe)
de chaque couloir. "x"
= 60 m ;
"y" = 100 m 1°)
Calculer la longueur du tour de piste
1. 2°)
Calculer la longueur du tour de piste 2. 3°)
Calculer la longueur du tour de piste 3.
4°) Si
l'on veut que le coureur "B" ligne 2 , parcourt
la même distance que le coureur "A" ligne 1 , il faut un
"décalage" entre les coureurs "A" et "B" (voir
figure) Calculer ce
décalage . 5°)
Montrer que le décalage entre les coureurs
A et B et le même qu'entre les coureurs "B" et "C" . |
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|