L’inégalité triangulaire.

La symétrie axiale .

Notions : plan –ligne – point

Matériel de traçage

Le nombre "pi"

La ligne courbe

Retour vers l’accueil « warmaths »

Objectif précédent  

1° )Le cercle .

2°)projection orthogonale d'un point sur une droite.

Objectif suivant :

1°)Les disques

2°) détermination du centre

3°)positions relatives de deux cercles

tableau   

Géométrie présentation

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

 Sciences     

Corrigé Contrôle 

Corrigé évaluation 

1 ° )Position relative d’un point / au cercle

2° ) Position relative d’une droite / cercle :

Extérieur 

Tangente

Sécante

TRACE d’un cercle :

Voir exercices CC

L’outil utilisé pour tracer un cercle est appelé : COMPAS

A) Positions relatives d’un point et d’un cercle 

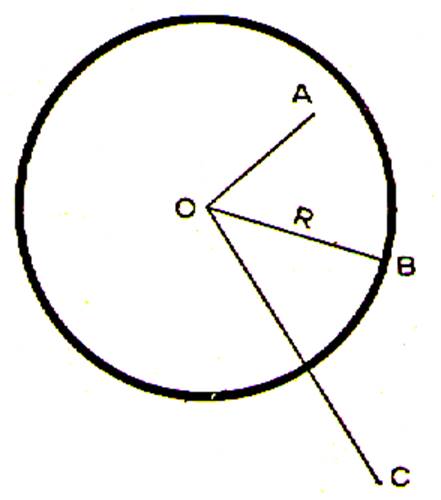
Un cercle partage le plan en deux régions .

L’intérieur du cercle .

L’extérieur du cercle qui ne contient pas le centre. On voit sur la figure qu’un point est à l’intérieur ou à l’extérieur du cercle suivant que sa distance au centre est inférieur ou supérieur au rayon.

Par contre tous les points du cercle ont la propriété commun d’être à la distance R du point O et ils sont  les seule points du plan qui possèdent cette propriété.

Pour cette raison on dit que le cercle de centre O et de rayon R est le lieu géométrique des points situés à la distance R  du point O .

B )  Positions relatives d’une droite et d’un cercle

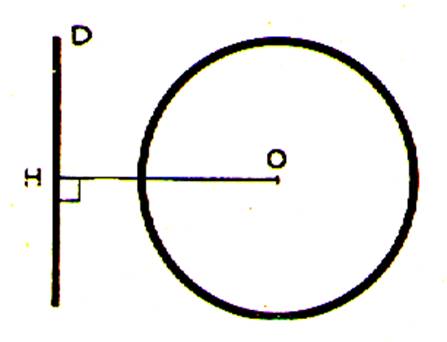
Pour chaque cas étudié :  O étant un point extérieur à une droite D , menons la perpendiculaire OH à la droite D ; elle mesure la distance d du point O à cette droite. Décrivons un cercle de centre O et de rayon R .

Suivant les grandeurs relatives de R et de « d » , nous obtenons trois figures différentes.

1 ° ) Droite extérieure

« d » > R

le point H est extérieur au cercle O ; or c’est le point de la droite D le plus proche de O.

 Il en résulte que tous les points de D sont extérieurs au cercle. On dit que la droite D est extérieur au cercle .

Droite tangente

Info plus : projection orthogonale et distance.

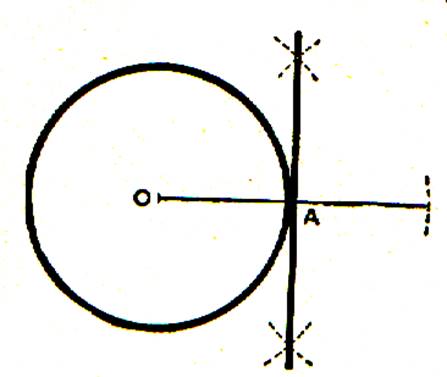
« d » = R

le point H est sur le cercle O , or c’est le point de la droite D le plus rapproché de O .Il en résulte que tous les autres points de D sont extérieurs au cercle. La droite D et le cercle  O ont un seul point commun. On dit que la droite D est tangente au cercle O.

remarque : on peut dire indifféremment que la tangente à un cercle rencontre celui-ci en un seul point ou qu’elle rencontre en deux points confondus.

Si une droite est tangente à un cercle tous ses points , à l’exception du point de contact est donc le plus petit segment joignant le centre O à un point quelconque de la tangente ; il est donc perpendiculaire à celle-ci .

: En géométrie encore , on pose cette définition :

  - La tangente à une courbe en un point donné de la courbe est la limite des positions d’une sécante, qui coupe la courbe en ce point et qui tourne autour de ce point de façon qu’un second point de section tende à se confondre avec le premier.

Construction de la tangente à un cercle en un point A de ce cercle.

Théorème :la tangente est perpendiculaire au rayon aboutissant au point de contact. On ne peut mener qu’une perpendiculaire à l’extrémité d’un rayon ; il en résulte que :

Théorème : par un point d’un cercle on ne peut mener qu’une tangente à ce cercle.

Tracer : à OA mener le rayon OA sur son prolongement ;tracer la perpendiculaire à ce rayon au point A .

Cercles tangents aux deux cotés d’un angle.

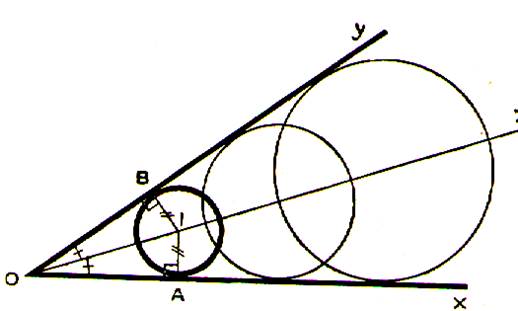
Un point quelconque I de la bissectrice intérieure d’un angle xOy est équidistant des cotés de cet angle.

 IA = IB

Il en résulte que le cercle de centre I etde rayon IA = IB sera tangent aux cotés de l’angle xOy .il y a donc une infinité de cercles tangents aux cotés d’un angle ; on peut choisir le centre n’importe où sur la bissectrice de l’angle.

Voir cercle inscrit dans un triangle

Droite sécante :

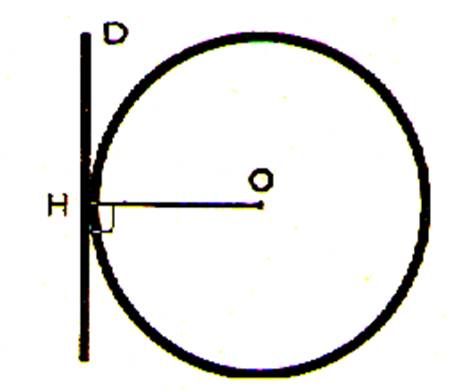
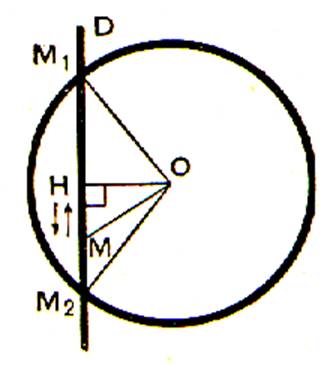
« d » < R

le point H est intérieur au cercle O ; par conséquent lorsqu’un  point M se déplace sur D de part et d’autre de H , l’oblique OM augmente depuis la valeur  d(<R) jusqu’à une valeur aussi grande qu’on le veut .Il existe donc , de part et d’autre de H , deux positions M₁ et M₂ du point M pour lesquelles .  OM₁ = OM₂  = R

la droite D et le centre O ont deux points commun et ne peuvent en avoir davantage. On dit que la droite D est sécante au cercle O.

Voir ++« Arc » , « corde »  

Voir ++ « flèche »