Pré requis:
|
|
|
|
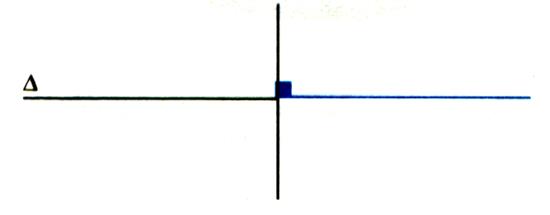
Tracé d’une perpendiculaire à une droite |
|
|
Les axes de symétrie : |
ENVIRONNEMENT du
dossier:
|
Objectif suivant |
DOSSIER « LES SYMETRIES »
SYMETRIE
ORTHOGONALE de figures simples
(dit
aussi : symétrie axiale )
-
Symétrie
orthogonale de figures simples et
propriétés
|
TEST |
COURS |
Interdisciplinarité |
|
INFORMATION
|
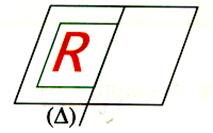
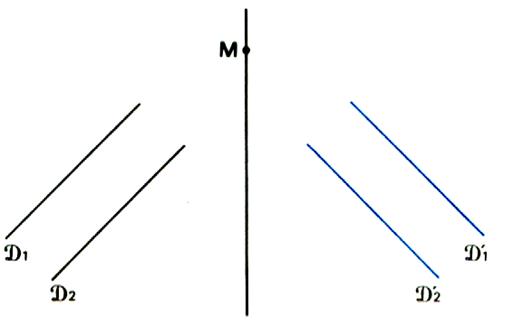
La rotation axiale
conduit à la symétrie axiale |
||
|
On calque R |
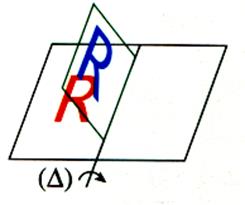
On fait tourner le caque
autour de (D) |
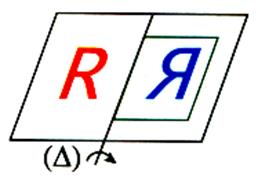
On obtient en bleu le
symétrique de R par rapport à la
droite (D) |
|
|
|
|
COURS :
Dans la Symétrie orthogonale de figures simples:
|
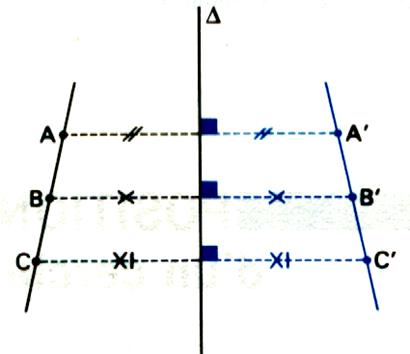
Dans un symétrie orthogonale par rapport à une
droite « delta » , si le point A
n’appartient par à « delta » , la point A
a pour image
le point A’ , Alors la droite « delta » est
perpendiculaire à ( AA’) et « delta » passe par le milieu du
segment [AA’] |
|
|
|
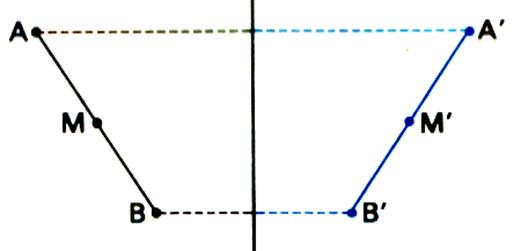
L’image d’une droite est une droite : Remarque : L’image du milieu d’un segment est le milieu du segment
« image » : M
milieu de [A,B] a pour image M’ milieu de [A’,B’] Une symétrie orthogonale conserve
les distances : d( A,M) = d ( A’,M’) d( M,B) = d ( M’,B’) d( A,B) = d ( A’,B’) |
|
|
|
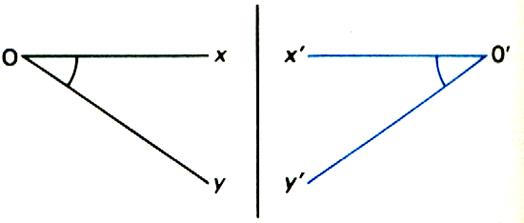
Une symétrie orthogonale conserve les angles.
|
|
|
|
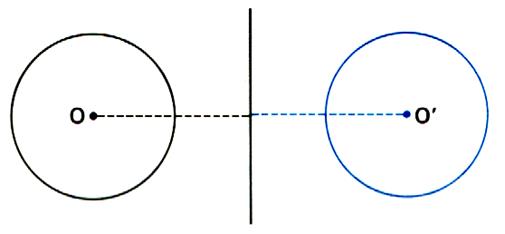
L'image d'un cercle de centre « O » est un cercle de même
rayon. Donc
: l'image d'un disque est un disque de même aire. Remarque :
si les deux cercles sont tangents ; la droite est tangente aux cercles .( elle est perpendiculaire au rayon ) |
|
|
|
La symétrie orthogonale d’un rectangle est un rectangle de mêmes
dimensions |
|
|
|
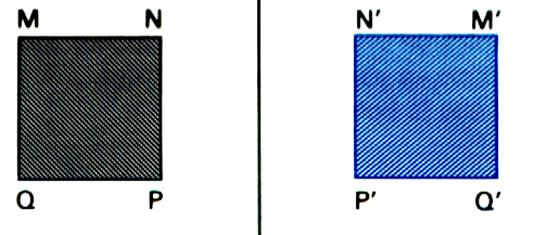
La symétrie orthogonale d’un carré est un carré de mêmes dimensions |
|
|
Donc un symétrie orthogonale
conserve les aires .
|
Deux droites parallèles ont pour images deux droites parallèles. Remarque : Si M est un point de l’axe ,
alors l’image de M dans la
symétrie est lui-même. Il en est de même pour tout
point de « delta » , c’est pourquoi nous
disons que « delta » est invariante dans la symétrie par rapport à
« delta ». |
|
|
|
La droite delta étant
perpendiculaire à
l’axe de symétrie a pour image elle-même |
|
|
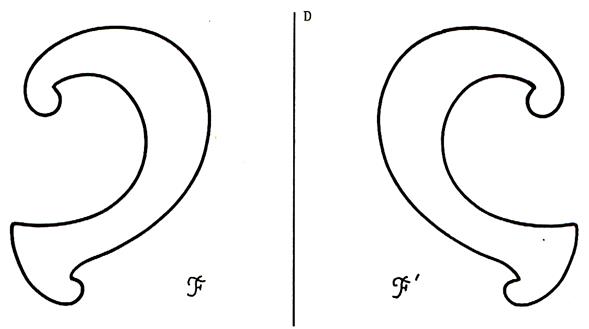
Exemple de figures symétriques par rapport à une droite « D ».
Si l’on dessine ces deux figures sur une feuille de calque ; on
remarque que ces figures se superposent.
La symétrie d’une figure
quelconque est cette figure quelconque.
|
|
EN
CONCLUSION:
Dans une symétrie orthogonale par rapport à une droite
« delta » , la droite « delta »
est appelée « axe de symétrie »
|
Une symétrie
orthogonale conserve : L'alignement
Les longueurs Les angles Il en résulte que toutes figures géométriques à pour image
une figure de mêmes dimensions , donc de même
aire. Une symétrie orthogonale conserve aussi : les aires . |
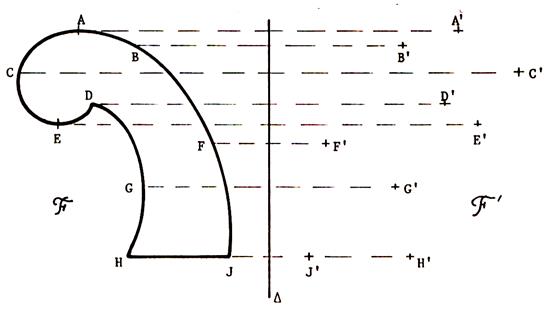
IMAGE d’ une figure dans une symétrie orthogonale.
Voici dans le plan ci dessous , une droite « delta » et une figure
« F »
|
|
L’image de « F » dans la symétrie orthogonale par rapport a « delta » est une figure « F’ »
constituée par l’ensemble des points qui sont les symétriques des points de
« F ».
Sur le
dessin ci-dessus , on a choisi quelques points de
« F » et on a déterminé leurs images .En imaginant que l’on fait la même chose pour
tous les points de « F » ,on peut compléter la figure
« F’ » .
Ainsi dans toute
symétrie orthogonale toute figure et son
image sont superposables. Ce qui
signifie que dans une symétrie orthogonale la figure et son image ont donc même
forme et mêmes dimensions.
|
Exemple
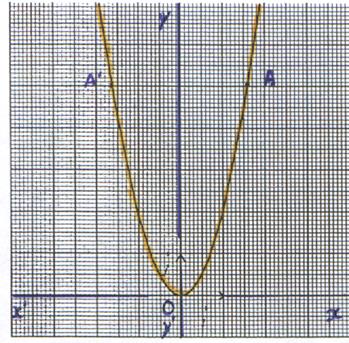
appliqué aux études de fonction : L’axe « y’ y » est axe de symétrie dans le tracé de la
fonction « x2 » Les points A’ et A sont
symétrique par rapport à « y’y »! ! |
|
CONTROLE
1°) Que
conserve une symétrie
orthogonale conserve ?:
Série1 :
|
Tracer la symétrie orthogonale |
|
|
|
|
|
|
|
- d’un segment de droite. |
|
|
|
-d’une droite. |
|
|
|
- d’un angle |
|
|
|
Tracer la symétrie orthogonale d’une figure
géométrique simple. |
|
|
|
|
|
|
|
Cercle |
|
|
|
Disque |
|
|
|
triangle |
|
|
|
Carré |
|
|
|
Rectangle |
|
|
Série 2 :
Construction
de l’image d’une figure :
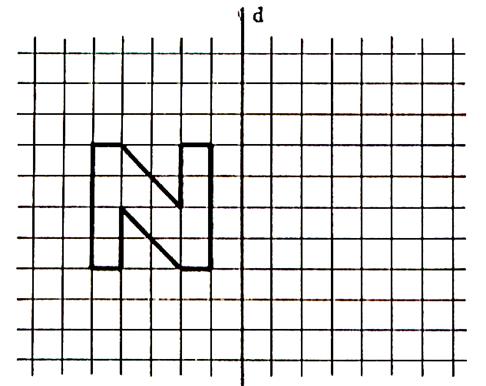
En utilisant le quadrillage , dans chacun des deux cas ,
dessiner les images des figures ci-dessous dans la symétrie orthogonale d’axe
« d »
|
1°)
|
|
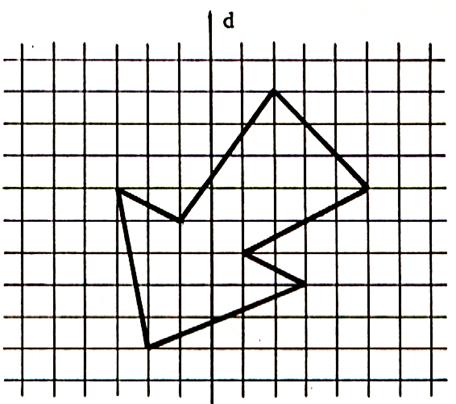
2°)
|
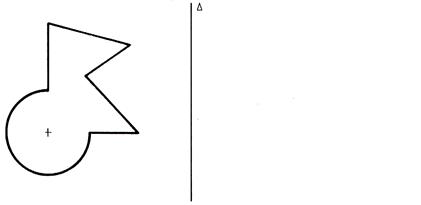
3°) Dessiner la figure ci-dessous
dans la symétrie orthogonale d’axe « delta » . Pour cela il faut déterminer l’image de certains points .
Laisser les droites
perpendiculaires à « delta » apparentes
|
|
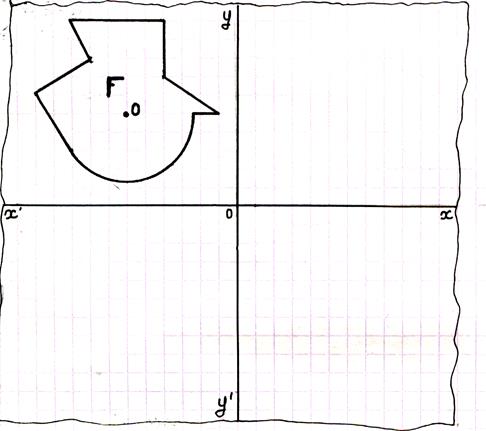
4° )COMPOSITION de deux
symétries orthogonales d’axes perpendiculaires.
xx’ et yy’ sont deux
droites perpendiculaires sécantes en « O ».Dessiner l’image F’ de la
figure « F » dans la symétrie
orthogonale d’axe x’x
puis l’image « F’’ » de la figure « F’ » dans la
symétrie orthogonale d’axe yy’ .
|
|