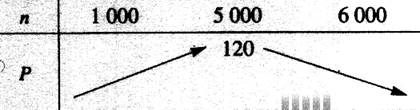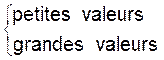PRE REQUIS
|
. |
|
|
|
|
|
|
|
|
. |
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant : 2°)
Etudes de fonctions numériques. |
|
|
|
|
|
|
|
DOSSIER : LES FONCTIONS N°1
Etude de la
représentation graphique d’une FONCTION NUMERIQUE.( généralités )
|
|
·
Rappels sur le tracé d’une fonction ou non fonction. |
. |
|
|
·
Etude du tracé d’une fonction. |
. |
|
|
·
Sens de variation (tableau de variation) |
. |
|
|
·
Maximum, minimum. |
. |
|
|
·
Parité. |
. |
|
|
·
Résumé : ce qu’il faut savoir faire lorsque l’on demande d’étudier
el graphique d’une fonction…. |
|
|
|
|
|
|
||||
|
|
|
Corrigé évaluation : |
|||||
Intérêt : savoir étudier un tracé
dans des matières interdisciplinaires (physique,chimie ,
géographie, histoire, statistique,….)
|
|
|
|
RAPPELS sur le tracé d’une fonction
ou non fonction. |
|
RAPPELS : Exemples de tracés
représentant une fonction :
|
|
|
|
|
A une valeur de « x » correspond au plus
une valeur de « y » |
Exemples de tracés ne représentant pas
une fonction :
|
|
|
|
|
A une valeur de « x » correspond plus
d’une valeur de « y » |
|
I )
Définition |
|
Lecture du symbole : la flèche « à
talon » elle remplace l’expression
« à pour image »
Soit une équation de la forme « y » égale
à une expression exprimée en fonction d’une variable
« x » : notée y = f(x)
Il y a « fonction » notée
« f » » si à un nombre
« x » on fait correspondre au
plus un nombre « y » .
On écrit
indifféremment :
|
f : x f(x) |
Lire : il y a
fonction ; où « x » à pour image « f(x) » |
|
|
f : x y |
Lire : il y a
fonction ; où « x » (en abscisse) a pour image « y » (en ordonnée) |
|
- « y » est obtenu par calcul ; on dit que
« y » est l’image de « x » ou que « x » fait correspondre « y ».
|
II )
REPRESENTATION GRAPHIQUE d’une fonction. |
Pour faire une représentation graphique ,on doit
faire des calculs , à partir de valeurs de « x ».
Plus on prendra de valeurs , plus on obtiendra
de « coordonnées » de points à placer dans un repère et plus le tracé de la courbe sera précis.
CHOIX
des valeurs de « x » et
« intervalle de définition ».
Les valeurs de « x » sont choisies, dans
des limites qui sont, ou non, fixées par
avance (ou imposées)
- Si ces limites ne sont pas imposées
, il n’y a pas « d’intervalle » qui fixent ces limites.
- Si ces limites
de « x » sont fixées (valeurs minimales et valeurs maximales
de « x »), on dit que l’on définit « un intervalle de calcul ou
d’étude ».
Cet intervalle (limité ou pas) est appelé « l’ensemble
de définition. »
|
|
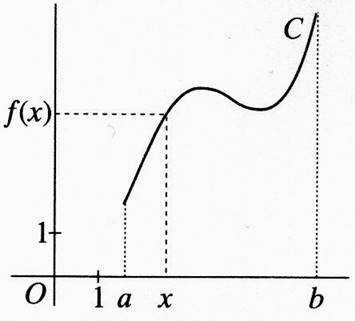
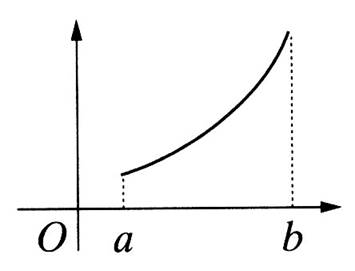
Le
tracé de la courbe est obtenue et
limitée par les valeurs de « x » appartenant à l’intervalle limité
par la valeur minimale « a » et la valeur maximale « b »
noté :[ a ; b] |
Exemple
d’application :
|
|
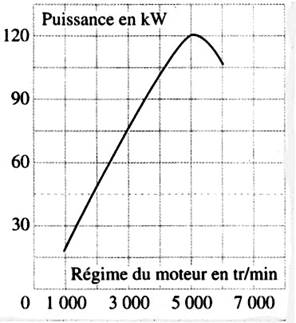
Ici
L’intervalle d’étude est
[1000 ; 6000 ] |
Procédure
à appliquer pour construire la représentation graphique d’une fonction :
- Rechercher des couples de valeurs ( x ; y ) avec l’équation y = f (x) ,
Au début , pour les premiers tracés ;ces valeurs seront
placés dans un tableau de
préférence .
|
x |
« x » |
Les
valeurs de « x » sont à choisir « judicieusement » |
Ligne des « Abscisses » |
|
0 |
|
|
y |
« f(x) » |
Ces valeurs sont obtenues par calculs (s.o.s calculs) |
Ligne des « ordonnées » |
|
f(0)= |
|
-
Placer les points de coordonnées ( x ;
y ) ; (coordonnées obtenues par calcul)
- Relier les points par une courbe « continue » ( ce peut être une droite si les points sont alignés)
|
|
La courbe obtenue est appelée : « courbe représentative » ou « représentation graphique » |
|
|
III ) ETUDE DE
LA REPRESENTATION GRAPHIQUE |
Exemple
d’application :
|
|
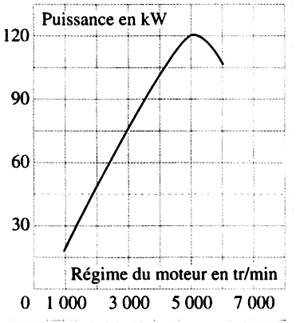
Ici
L’intervalle d’étude est
[1000 ; 6000 ]. On remarque qu’entre 1000 et 5000 tr/
min la puissance du moteur augmente,
et qu’entre 5000 et 6000 tr/min la puissance diminue. On constate qu’à 5 000 tr/min la
puissance est maximum.(120 kW ) Nous pouvons résumé
ces variations par le tableau suivant :
les flèches indique
le sens de variation de la fonction. |
|
A) DETERMINATION DU SENS DE VARIATION (tableau de variation). |
Dans un
intervalle donné I = [a ;b] ;on
peut rencontrer 3 possibilités
Le « sens de variation » est indiqué dans un tableau dit de variation.
I)
La fonction est CROISSANTE.
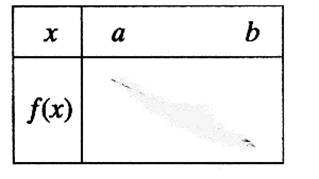
Une
fonction est dite croissante sur un intervalle [ a ;
b ] si les valeurs de « y » augmentent quand celles de
« x » augmentent.
|
|
|
|
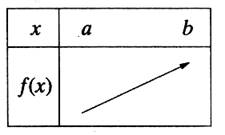
On établit le tableau de variation suivant : La flèche indique le sens de variation de la
fonction.
|
Si pour tous nombres x1 et x2
d’un intervalle I = [a ;b], tels que x1 < x2 . et si
f ( x1 ) £ f (x2) ,on peut
dire alors que la fonction est
croissante sur I (%º@ Par le
calcul :calcul du taux d’accroissement.) |
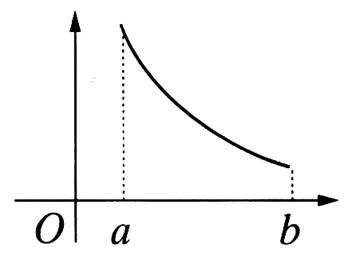
II)
La fonction
est DECROISSANTE.
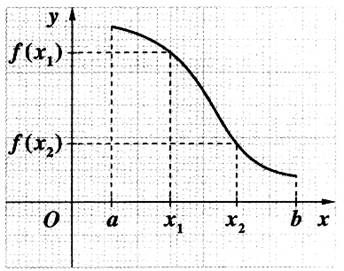
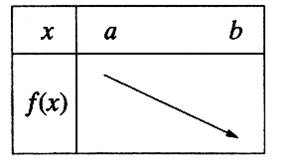
Une fonction est dite « décroissante » sur un intervalle [ a ; b ] si les valeurs de « y » diminuent
quand celles de « x » augmentent.
|
|
|
|
|
On établit le tableau de variation suivant : La flèche indique le sens de variation de la fonction.
|
Si pour tous nombres x1 et x2
d’un intervalle I = [a ;b], tels que x1 < x2 . et si
f ( x1 ) ³ f (x2) ,on peut
dire alors que la fonction est
décroissante sur I ((%º@ Par le
calcul :calcul du taux d’accroissement.) |
|
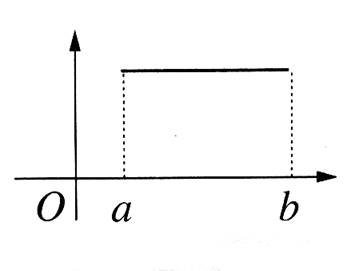
III ) La fonction est CONSTANTE.
Une
fonction est dite « constante » sur un intervalle [
a ; b ] si la valeur de « y » est constante quand
« x » varie.
|
|
|
|
On établit le tableau de variation suivant : La
flèche indique le sens de variation de la fonction.
|
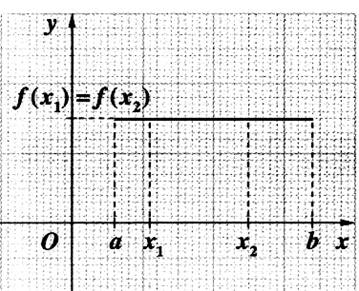
Si pour tous nombres x1 et x2 d’un intervalle I
= [a ;b], tels que x1 < x2 . et si
f ( x1 ) = f
(x2) ,on peut dire alors
que la fonction est constante sur I ((%º@ Par le
calcul :calcul du taux d’accroissement.) |
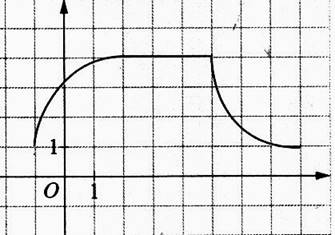
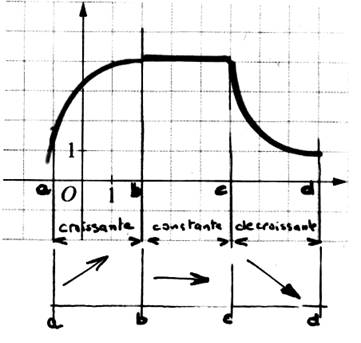
Exemple d’ étude d’un tracé:
|
- On identifie des segments différents. - On détermine des intervalles. - Dans un tableau , on indique par une
flèche, si dans l’intervalle choisi la fonction est croissante ,
décroissante, ou constante. |
|
INFO : On peut connaître le sens de
variation d’une fonction, par le calcul ,il faut
savoir calculer , dans un intervalle donné ,« le nombre dérivé » et
étudier le signe (+ ou - ) de ce nombre.
Ce nombre dérivé est aussi appelé « taux d’accroissement ».Savoir calculer ce nombre dérivé (via le taux d’accroissement)
c’est savoir calculer la pente (tangente) d’un
triangle rectangle.
(évidemment : pour qu’un triangle soit
rectangle dans un repère
,il faut que le repère soit orthogonal)
|
B) RECHERCHE d’un MAXIMUM ou MINIMUM sur le
graphique. |
Préambule :
Certaines fonctions croissent puis décroissent,et vis versa, par exemple
lorsque le tracé est une parabole, on dit que la
fonction passe un point maximum ou un point minimum.
Ce point est identifiable sur un tracé, c’est
le point le plus haut ou le plus bas de la courbe et les coordonnées sont
relevables sur le tracé.
|
Exemples
types :
de la fonction dite « polynomiale » du second degré. ( type : y = a x² + bx + c
) Les
tracés de ces types de fonctions sont des courbes appelées : paraboles. Remarque :
les fonctions du type f(x) = a x² ont la même forme de courbe… |
|
|
|
|
Pour
informations :
En
absence du tracé de la courbe , Comment rechercher les
coordonnées du point « maxima » ou « minima » ? :
Ces coordonnées peuvent être obtenues par
calculs ; Il faut savoir
1°) calculer « une tangente »
2°) calculer le taux d’accroissement et
étudier ce que devient ce taux d’accroissement au voisinage du point de « changement de
pente ». (ce qui implique de connaître la notion
de limite lorsque l’on veut que
f(x)/x tend vers 0).
3°) Il faut apprendre à calculer de la dérivée
d’une équation ……….(nous
verrons cela au niveau III)
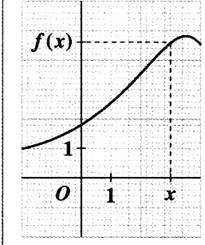
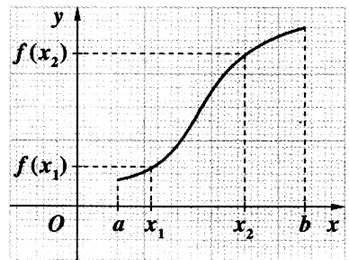
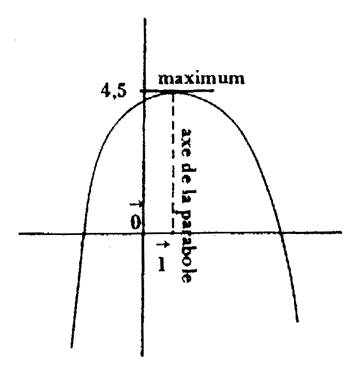
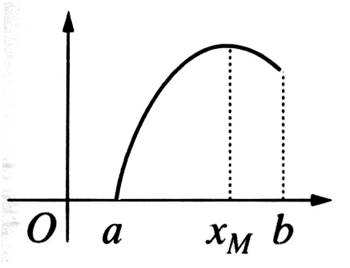
1°) MAXIMUM :
On appelle « maximum » la valeur
maximale atteinte par f(x). On dit que la fonction « f » atteint un
maximum en « x M »
|
Représentation graphique : |
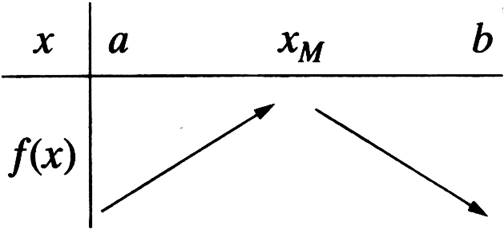
Il s’en suit le tableau de variation ci -
dessous : La fonction croit [a ; x M
] et décroît dans
l’intervalle [ x M ; b]] |
|
|
|
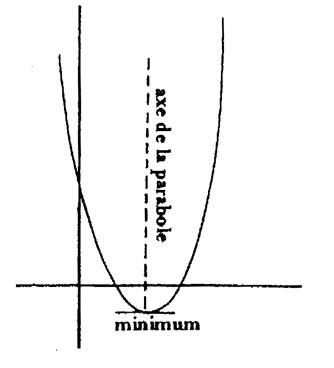
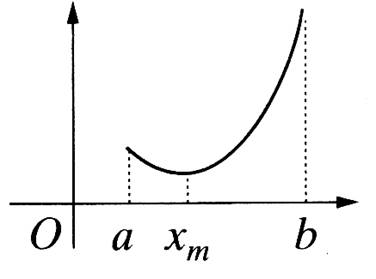
2°) MINIMUM :
On appelle « minimum» la valeur minimale
atteinte par f(x). On dit que la fonction « f » atteint un minimum en
« x m »
|
Exemple de représentation graphique : |
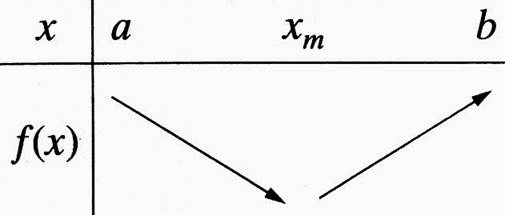
Il s’en suit le tableau de variation ci -
dessous : La fonction croit [a ; x m ] et
décroît dans l’intervalle [ x m ; b]] |
|
|
|
|
INFO :Symétrie
centrale. |
RECHERCHE de la PARITE (en lecture sur le graphique) |
Par le calcul |
On dit qu’une fonction, peut
être, « paire » ou « impaire ».Cette parité est
remarquable sur un tracé.
1°) Fonction « paire » :
Pour affirmer qu’une fonction est
« paire » on peut soit le montrer
par le calcul ; soit sur le vérifier sur le tracé.
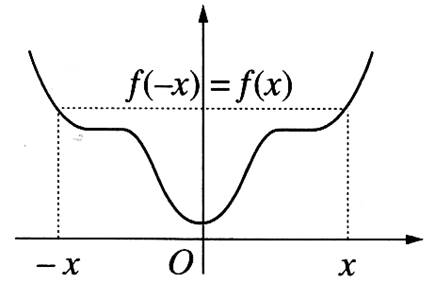
a) Par le calcul : Une
fonction est dite « paire » si
pour toutes les valeurs de « x » : f (-x) = f (x)
Ce qui se montre par le calcul (exemple la courbe de f(x) = x²)
b)
le tracé : La courbe représentative d’une
fonction « paire » admet l’axe des ordonnées pour axe de symétrie.
|
|
|
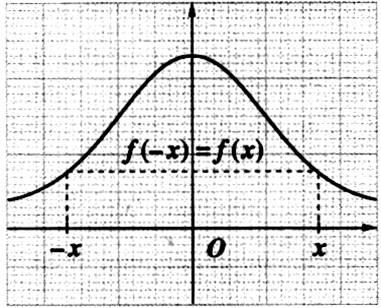
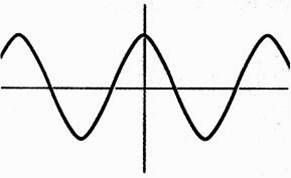
Cas
des fonctions périodiques: la courbe de la fonction cosinus (
appelée : sinusoïde)
|
Cette représentation graphique est le tracé
d’une fonction dite « périodique ». La courbe sinusoïde de la fonction cosinus
est symétrique par rapport à l’axe des ordonnées, elle est
« paire ». |
|
.
2°) Fonction
« impaire » : Pour affirmer qu’une fonction est «im paire » on peut soit le montrer par le calcul ; soit sur le vérifier sur
le tracé.
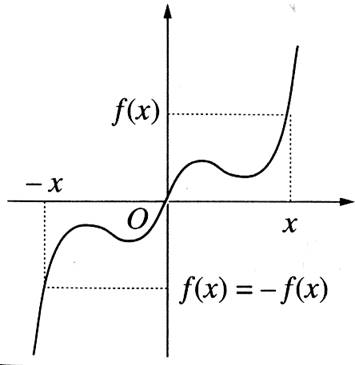
a)
Par le calcul : Une fonction
est dite « impaire » si, pour
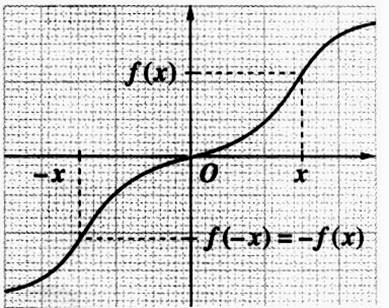
toutes les valeurs de « x » :f (-x) = - f (x)
Ce qui se montre par le calcul (exemple la courbe de f(x) = x3)
La courbe représentative d’une fonction
« impaire » admet l’ origine « O »
du repère pour entre de symétrie.
|
|
|
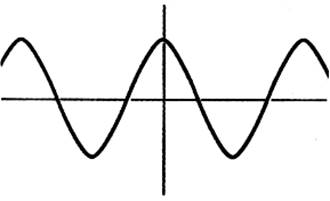
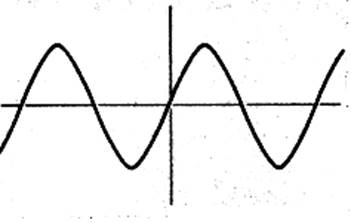
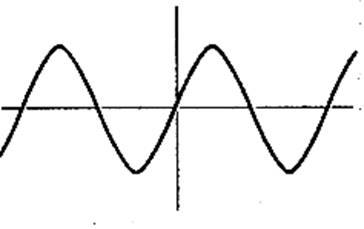
Cas des
fonctions périodiques: la courbe de la fonction sinus (
appelée : sinusoïde)
|
Cette représentation graphique est le tracé
d’une fonction dite « périodique ». La courbe sinusoïde de la fonction sinus est
symétrique par rapport à l’origine « O » du repère
, elle est «impaire ». |
|
|
C) IDENTIFIER si une FONCTION PERIODIQUE. |
|
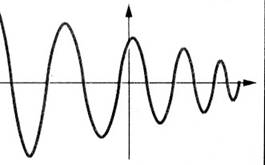
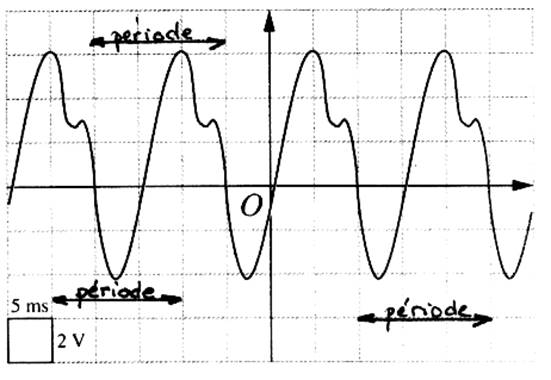
Ce type de fonction est rencontrée en
science :le tracé d’une telle fonction est
obtenue par un oscilloscope.(courant alternatif)
Le
courant électrique alternatif est visualisé sur l’écran d’un oscilloscope .ll en est de même
pour le son émis par un appareil.
En réalité , l’oscilloscope
visualise la variation d’une tension en fonction du temps.
|
Une fonction est dite
« périodique » si dans un intervalle donné le tracé de la courbe se
reproduit, indéfiniment. La période est mesurée sur l’axe de la variable « temps ».Elle est généralement
« T ». |
|
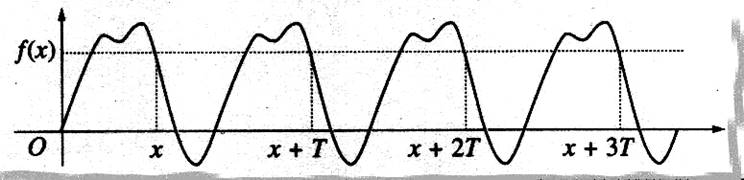
Exemple :
|
La fonction est périodique de période
« T » si : f(x) = f (x+T)= f (x+2T)= f (x+3T)= …. |
|
|
|
|
Les fonctions périodiques les plus simples étudiées sont les sinusoïdes.
|
Fonction « sinus » (fonction impaire) |
onction « cosinus » (fonction paire) |
INFO : MOTS CLEFS : l’ensemble de définition ;taux d’accroissement, tableau
de variation , représentation graphique ; utiliser le repère cartésien . le
plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )
EN RESUME :
Lorsque l’on vous demande
d’ étudier la représentation graphique d’une fonction
on doit :
-1°) Savoir
Identifier, par la forme du tracé, le type de l’équation qui à permis de réaliser ce tracé..(l’allure de la
courbe) : linéaire, affine , du second degré, du troisième degré , racine
, inverse (homographique), sinusoïde
représentant un sinus ou un cosinus ;…..Il savoir dire si la
fonction est périodique ou non périodique.
- 2°) Identifier
ce qui caractérise le tracé d’« une
fonction ».
-Savoir donner
le domaine de définition. (pour quelles valeurs
de « x » le tracé sera le
représentant de la fonction)
- Savoir identifier les
bornes des intervalles de « x ». ou savoir donner les valeurs mini et maxi de
« x » qui limite l’étude du tracé .
- Savoir identifier dans
un intervalle donné, l’allure de la
courbe. Dire si la fonction est croissant, décroissante,
constante.
- Dans un tracé continu d’une fonction pouvant être successivement :
« croissant », « décroissant », « constant », il
faut savoir identifier le point de passage de changement de
« pente » : Est-il « maximum » ou
« minimum ». et éventuellement quelles sont les coordonnées de ce
point ?
- 3°) Pour rendre
compte de l’étude d’une fonction (observation sur le tracé) il faut savoir construire
et compléter et remplir un tableau de variation.
Pour « x » :
- on indiquera :
«les valeurs des bornes de chaque intervalle»,
- la valeur de
« x » qui indique un changement de pente.
- Si la courbe coupe
l’axe des « x » on donnera l’ abscisse ou
les abscisses de ces points.
Pour f(x) :
- pour les valeurs particulières de « x » on calculera
les valeurs « f(x) » correspondantes. De ces valeurs partira et
arrivera la flèche
4°) On complétera l’étude en indiquant
-
si la fonction est « paire » ou
« impaire ».
-
si elle est périodique (ou non périodique)
|
|
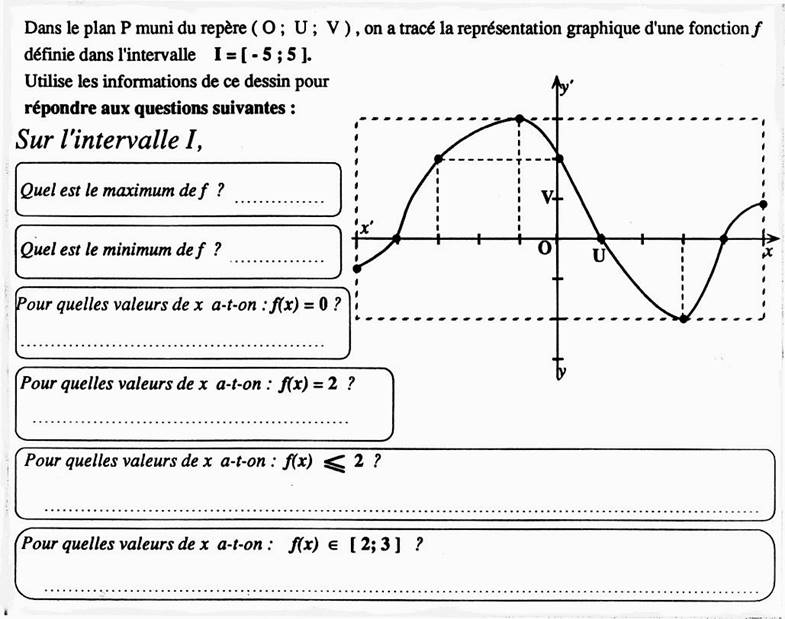
Exemple d’application : |
|
|
|
|
|
Maximum de f = 3 Minimum de f = - 3 f(x) = : - 4 ; 1 ; 4 f(x) = 2 ; 0 et - 3 f (x) £
2 : x Î [ - 5 ; - 3 ] È [ 0 ; 5 ) ] f (x) Î [ 2 ; 3 ] ;
réponse : x Î [ -
3 ; 0 ] |
TRAVAUX AUTO FORMATIFS.
CONTROLE:
1°) Sur quelles caractéristiques peut
porter l’étude de la
représentation graphique d’une fonction ?
(Préciser pour chaque caractère)
|
|
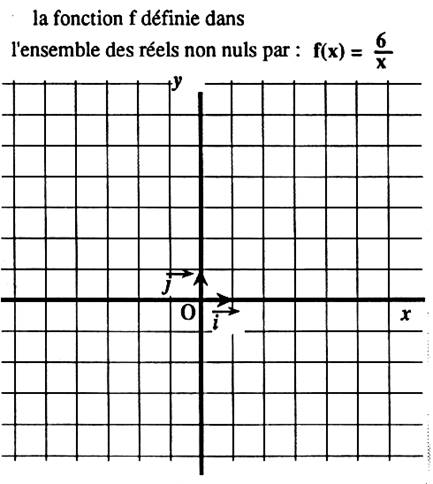
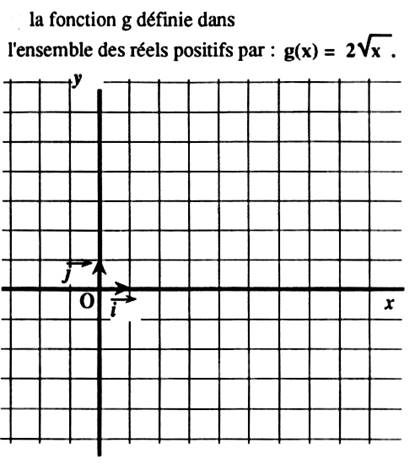
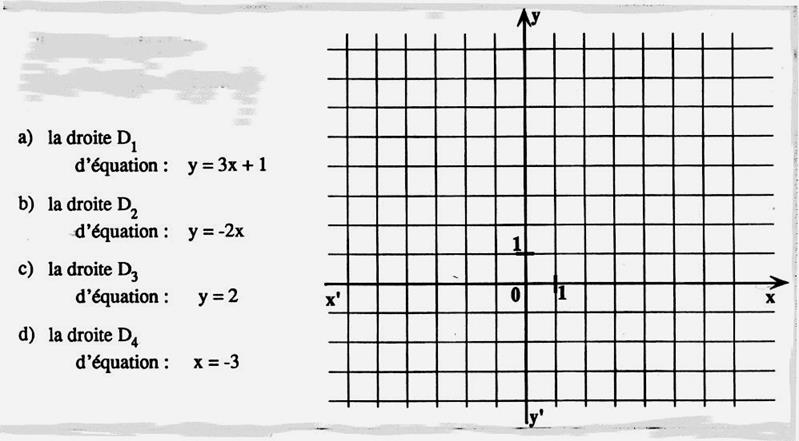
N°1 : Utiliser les quadrillages pour représenter graphiquement les fonctions
suivantes : |
|||
|
|
|
|
|
|
|
|
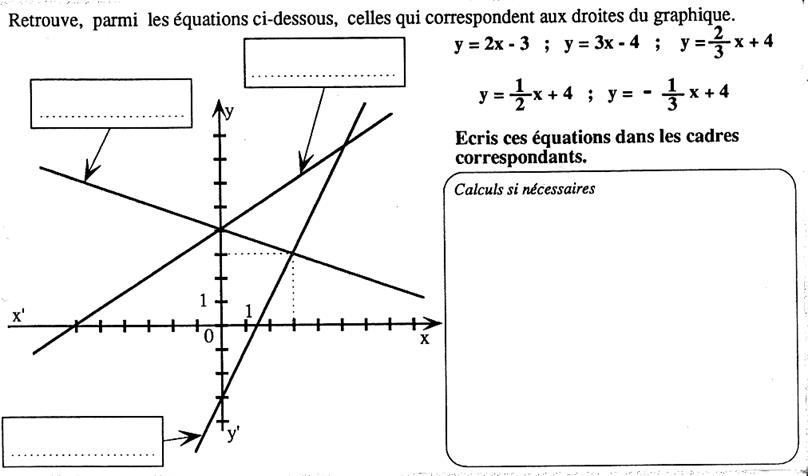
Donner le sens de variation des
fonctions « f » et « g » sur les intervalles indiqués, en
complétant les phrases suivantes : Sur [ 1 ;
6 ] ; « f » est une fonction ……………………………………………. Sur [ 0 ;
5 ] ; « g » est une fonction ……………………………………………… Toujours à propos des fonction
« f » et « g » , dans chacun des
cas ci - dessous, entourer la réponse qui convient et barrer l’autre : Pour les petites valeurs positives de « x » , f(x) prend des : Pour les grandes valeurs
positives de « x » , f(x) prend
des : Pour les grandes valeurs positives de « x » , g(x) prend des : |
|||
|
|
N°2 ( SOS Corrigé) |
|
|
|
|
|
|
|
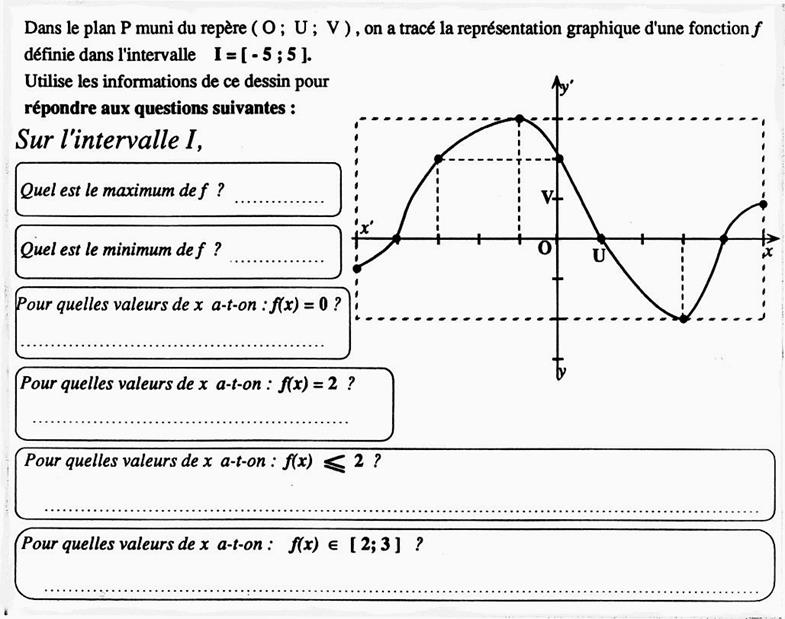
N°3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
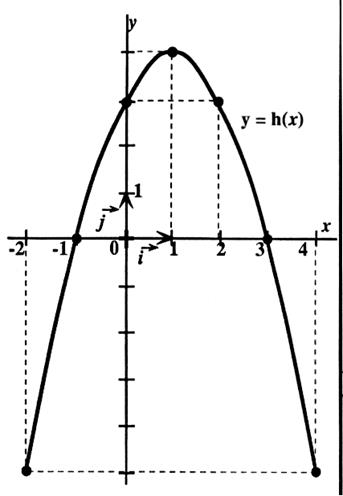
Voici la représentation graphique d’une fonction « h »
définie sur l’intervalle [ - 2 ; 4 ] Utiliser le graphique pour répondre aux questions suivantes : On notera que le point « · »
sont sur la courbe et ont pour
coordonnées des nombres entiers. 1°) Dresser le tableau de
variation de « h » 2°) Donner les solutions de l’équation : h (x) = 0 3°) Etudier le signe de h(x) sur l’intervalle [ -
2 ; 1] 4°) Donner l’ensemble des solutions
de l’inéquation : h(x) ³ 3 |
|
|
|
|
|
|
|
|
ACTIVITES
COMPLEMENTAIRES :
|
LES FONCTIONS : |
|||||||
|
I
) Génération et description des fonctions |
Liste des tests |
||||||
|
|
a) exemples de modes de génération de fonctions. |
|
|
|
|
|
|
|
|
Exemples de description d’une situation à l’aide d’une fonction. |
|
|
|
|
|
|
|
|
Représentation graphique d’une fonction dans un repère ortho
normal ou orthogonal. |
|
|
|
|
|
|
|
|
b) Exemples simples de calculs de valeurs d’une fonction à l’aide
d’une calculatrice. |
|
|
|
|
|
|
|
|
c) Parité , périodicité. : maximum , minimum d’une fonction, fonctions croissantes,
fonction décroissantes |
|
|
|
|
||
|
|
d) exemples de lecture de propriétés de fonctions à partir de leur
représentation graphique. |
|
|
|
|
||
|
II
) Fonctions usuelles. |
Liste des tests |
||||||
|
|
a) Variations et représentation graphiques des fonction : x ® a x + b ; x ® x² ; x ® x 3 ; x ® |
|
|||||
|
|
b) Exemples simples d’études de comportements de fonctions tels
que : signe ,
variations, recherche de maximum et de minimums, représentations graphiques
dans un repère (orthonormal ou orthogonal). |
|
|
|
|||
|
|
c) Exemples simples d’étude graphique d’équation de la forme f (x) = l où l a une valeur numérique donnée. |
|
|
|
|||
|
|
d)Etude des
fonctions cosinus et sinus : périodicité ,
symétries, sens de variation. Courbes représentatives. |
|
|
|
|||
|
|
|
|
|
|
|
|
|