Pré requis:
|
Les Fonctions numériques |
ENVIRONNEMENT du dossier:
|
Objectif précédent |
Objectif suivant |
DOSSIER : Etudes des FONCTIONS USUELLES (niveau 5et 4 )
1 - ETUDE TYPE D’
UNE FONCTION :
2 - Exemples
d’étude de LA FONCTION LINEAIRE :
· Exemple 1 f : x ![]() - 3x
- 3x
·
Exemple 2 f : x ![]() 2x
2x
· Cas général : f : x ![]() ax
ax
3 - Etude de
la FONCTION
AFFINE : f : x![]() a
x+ b
a
x+ b
·
Exemple 1 : f : x ![]() 2 x+ 1
2 x+ 1
·
Exemple 2 :
f : x ![]() -
- ![]() x
+1
x
+1
·
Cas général : f : x![]() a
x + b
a
x + b
4- ETUDE DE
LA FONCTION
MONOME du second degré : f :
x![]() ax2
ax2
· Exemple 1 f : x
![]() 1 x 2
1 x 2
·
Exemple 2: f : x ![]() -
0, 5 x2
-
0, 5 x2
· Exemple 3 f : x ![]() 2x2
2x2
5- Etude
de la FONCTION MONOME du
troisième degré : f : x![]() ax3
ax3
6- ETUDE
DE LA FONCTION racine
carrée : f : x ![]()
![]()
7 -ETUDE DE LA FONCTION
homographique : f : x ![]()
![]()
9- Comparaison de deux
fonctions
10 - Fonction se
déduisant d’une fonction usuelle par addition d’une constante.
Liste des fonctions :
|
Exemples de f : R |
Nom de fonction |
Info++ |
|
x |
|
|
|
x |
||
|
x |
Fonction monôme du second degré |
|
|
x |
Fonction monôme du troisième degré |
|
|
x |
Fonction racine carrée |
|
|
x |
Fonction homographique |
|
TEST |
COURS |
Interdisciplinarité |
|
COURS
1 - ETUDE TYPE D’ UNE
FONCTION :
Etudier une
fonction c’est :
A partir de f :
R ![]() R
R
x ![]() f
(x)
f
(x)
1°) Donner l’ensemble de définition.
2°) Faire une étude aux
bornes du domaine de définition :
a) que se passe-t-il
pour f (x) quand « x » tend vers -¥ ?
b) que se passe-t-il
pour f (x) quand « x » tend vers +¥ ?
c) que se passe-t-il
pour f (x) quand « x » = 0
d) résoudre f (x) =
o
3°) Donner le sens de variation :
il faudrait calculer le taux d’accroissement
4°) Construire le tableau
de variation :
type
|
x |
-¥
0
+¥ |
|
|
? ? ? ? ?sens donner avec des flèches |
5°) Faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le repère
cartésien orthonormé ( dit aussi « orthonormal »
)
Repère cartésien
|
|
2 - Exemples d’étude de LA FONCTION LINEAIRE :
Exemple
1 f : x |
f : R ![]() R
R
x![]() -3x
-3x
1°)Ensemble de définition.
Df = R
2°)Etude aux bornes du domaine de définition Df:
a) que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x)
tend vers +¥ quand « x » tend vers -¥
b) que se passe-t-il pour f
(x) quand « x » tend vers +¥ ?
f (x) tend
vers -¥ quand « x » tend vers +¥
c) que se passe-t-il pour f
(x) quand « x » = 0
f (o) = o
d) résoudre f (x) = o
0 =
-3 x donc x = 0
3°)Sens de variation :
Calculer le taux d’accroissement : pas nécessaire le taux
correspond à « a »
le
coefficient de « x » est négatif
( a = -3 ) , f est donc strictement décroissante dur Df
4°) le tableau de
variation :
|
x |
-¥ 0 +¥ |
|
|
+¥
0
-¥ |
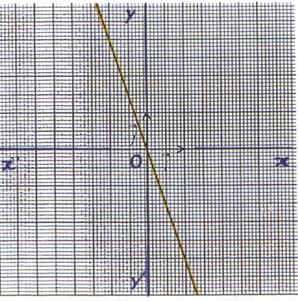
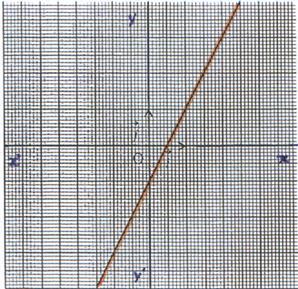
5°) Représentation graphique :
|
La représentation graphique de la fonction f est
une droite d’équation y = -3x passant par l’origine du repère et le
point de coordonnées (1 ; -3 ) |
|
Exemple 2 : f : x |
INFORMATIONS +++ |
f : R ![]() R
R
x ![]() 2x
2x
1°)Ensemble de définition. Df
= R
2°)Etude aux bornes du domaine de définition Df:
b) que se passe-t-il pour f (x) quand
« x » tend vers -¥ ?
f (x) tend vers +¥
quand « x » tend vers +¥
b) que se passe-t-il
pour f (x) quand « x » tend vers +¥ ?
f (x) tend vers -¥
quand « x » tend vers -¥
c) que se passe-t-il
pour f (x) quand « x » = 0
f (o) = o
d) résoudre f (x) =
o 0 = 2 x donc x = 0
3°)Sens de variation :
calculer le taux d’accroissement :
pas nécessaire le taux correspond à
« a »
le coefficient de
« x » est négatif ( a = 2 ) ,
f est donc strictement croissante sur Df
4°) le tableau de
variation :
|
x |
-¥
0
+¥ |
|
|
+¥ 0 -¥ |
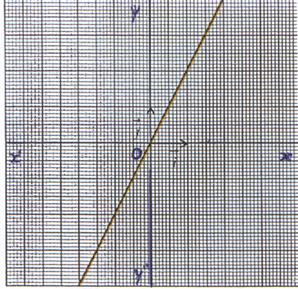
5°) Représentation graphique :
|
La représentation graphique de la fonction f est
une droite d’équation y = 2x passant par l’origine du repère et le
point de coordonnées (1 ; 2 ) |
|
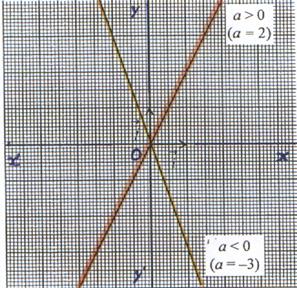
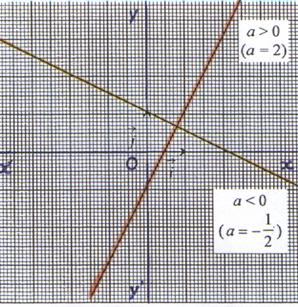
Cas général : FONCTION LINEAIRE : de
la forme : f : x![]() ax
ax
|
|
f :
R ![]() R
R
x![]() ax
ax
1°)Ensemble de définition. Df
= R
2°)Etude aux bornes du domaine de définition Df:
|
a < 0 |
a
> 0 |
|
f
(x) tend vers +¥ quand « x » tend vers -¥ f
(x) tend vers -¥ quand « x » tend vers +¥ f
(o) = o |
f (x) tend vers +¥ quand « x » tend
vers +¥ f (x) tend vers -¥ quand
« x » tend vers -¥ f (o) = o |
3°)Sens de variation :
|
a < 0 |
a
> 0 |
|
f est donc strictement décroissante sur Df |
f
est donc strictement croissante sur Df |
4°) le tableau de
variation :
|
a < 0 |
|
a
> 0 |
||
|
x |
-¥ 0 +¥ |
|
x |
-¥ 0 +¥ |
|
|
+¥ 0
-¥ |
|
f(x) |
+¥ 0 -¥ |
5°) Représentation graphique :
|
La représentation graphique de la fonction f est
une droite d’équation y = ax passant par l’origine du repère et le
point de coordonnées (1 ; a ) |
|
|
3 - Etude de la FONCTION AFFINE : f :
x |
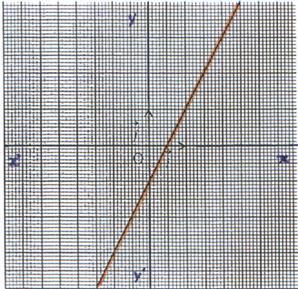
Exemple 1 :
f : x![]() 2
x+ 1
2
x+ 1
f : R ![]() R
R
x ![]() 2 x
- 1
2 x
- 1
1°)Ensemble
de définition. Df = R
2°)Etude
aux bornes du domaine de définition Df:
c)
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x) tend vers -¥ quand « x » tend vers -¥
b) que se passe-t-il pour f
(x) quand « x » tend vers +¥ ?
f (x) tend vers +¥ quand « x » tend vers +¥
c) que se passe-t-il pour f
(x) quand « x » = 0
f (o) = 1
d) résoudre f (x) = o 0 =
2 x-1 donc x = ![]()
3°)Sens
de variation :
calculer
le taux d’accroissement : pas nécessaire le taux correspond à « a »
le coefficient de
« x » est négatif ( a = 2 ) ,
f est donc strictement décroissante sur Df
4°) le tableau de variation :
|
x |
-¥ 0 +¥ |
|
|
+¥ -1 -¥ |
|
5°)
Représentation graphique : La représentation graphique de la
fonction f est une droite d’équation y
= 2x-1 passant par l’origine du repère et le point de coordonnées (0 ;
-1 ) et le point de coordonnées ( |
|
|
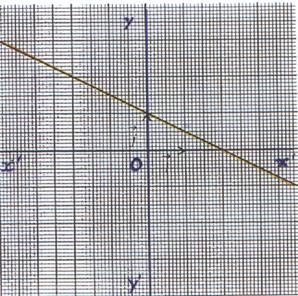
Exemple 2 FONCTION AFFINE : x |
f : R ![]() R
R
x ![]() -
- ![]() x
+1
x
+1
1°)Ensemble de définition. Df = R
2°)Etude aux bornes du domaine de définition Df:
d) que se passe-t-il pour f (x)
quand « x » tend vers -¥ ?
f
(x) tend vers +¥
quand « x » tend vers -¥
b)
que se passe-t-il pour f (x) quand « x » tend vers +¥ ?
f
(x) tend vers -¥
quand « x » tend vers +¥
c)
que se passe-t-il pour f (x) quand « x » = 0
f
(o) = 1
d)
résoudre f (x) = o 0 = -![]() x +1
donc x = 2
x +1
donc x = 2
3°)Sens de
variation :
calculer le taux d’accroissement :
pas nécessaire le taux correspond à
« a »
le coefficient de « x » est négatif ( a = -![]() ) , f est donc strictement décroissante sur Df
) , f est donc strictement décroissante sur Df
4°) le
tableau de variation :
|
x |
-¥
0
+¥ |
|
|
+¥ 1
-¥ |
|
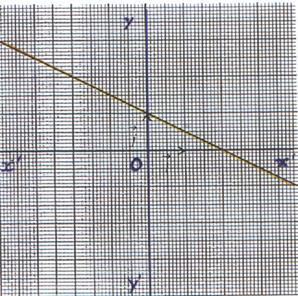
5°) Représentation graphique : La
représentation graphique de la fonction f est une droite d’équation y = - |
|
f : R ![]() R
R
x ![]() a x
+ b
a x
+ b
1°) Ensemble de définition. Df = R
2°) Etude aux bornes du domaine de
définition Df:
|
a < 0 |
a
> 0 |
|
f
(x) tend vers +¥ quand « x » tend vers -¥ f
(x) tend vers -¥ quand « x » tend vers +¥ f
(o) = b |
f (x) tend vers +¥ quand « x » tend
vers +¥ f (x) tend vers -¥ quand
« x » tend vers -¥ f (o) = b |
3°)Sens de
variation :
|
a < 0 |
a
> 0 |
|
f est donc strictement décroissante sur Df |
f est donc strictement croissante sur Df |
4°) le
tableau de variation :
|
a < 0 |
|
a
> 0 |
||
|
x |
-¥ 0 +¥ |
|
x |
-¥ 0 +¥ |
|
|
+¥ b
-¥ |
|
f(x) |
+¥ b -¥ |
|
5°) Représentation graphique : La
représentation graphique de la fonction f est une droite d’équation y = ax + b
passant par les points de
coordonnées : (
0 ; b ) ; (1 ; a + b
) et (- |
|
|
4- ETUDE DE LA FONCTION MONOME du second degré : f :
x |
Exemple 1 :
x ![]() 1 x 2
1 x 2
f : R ![]() R
R
x ![]() x2
x2
1°)Ensemble
de définition. Df = R
2°)particularité :
(est-elle paire ou impaire ? )
quel
que soit le réel « x » appartenant à Df f(-x) = (-x2) = x2 =f(x) ; f est donc « paire »
3°
) Etude aux bornes du domaine de définition Df:
e)
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x) tend vers +¥ quand « x » tend vers -¥
b) que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f (x) tend vers -¥ quand « x » tend vers -¥
c) que se passe-t-il pour f (x)
quand « x » = 0
f (o) = o
d) résoudre f (x) = o 0 =
x2 donc x = 0
4°)Sens
de variation :
voir
le calcul du taux correspond à « a »
f est donc strictement décroissante sur
R- et strictement croissante
sur R+
5°) le tableau de variation :
|
x |
-¥ 0 +¥ |
|
|
+¥
+¥ 0 |
f admet
un minimum égal à 0 pour x = 0
|
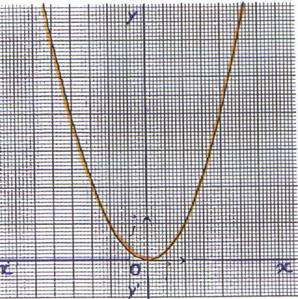
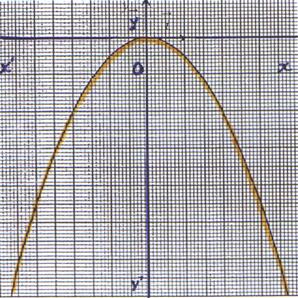
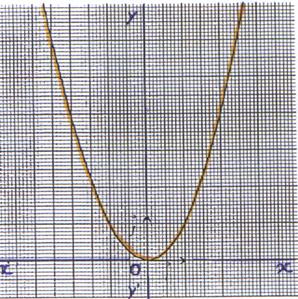
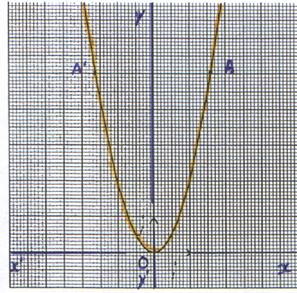
6°)
Représentation graphique : La représentation graphique de la
fonction f est une parabole d’équation
y
= x2 , de sommet O (
0 ;0 ) , admettant l’axe (y’ y ) comme axe de symétrie et l’axe
« x’ x » ) comme tangente au sommet . |
|
Fonction
se déduisant d’une fonction usuelle par multiplication par une constante .
Soit
« a » un nombre réel et une fonction numérique f de R vers R.
-
si a > 0
, les fonctions x![]() f (
x) et x
f (
x) et x![]() a f
( x) ont le même sens de variation.
a f
( x) ont le même sens de variation.
-
si a < 0
, les fonctions x![]() f (
x) et x
f (
x) et x![]() a f
( x) varient en sens contraire .
a f
( x) varient en sens contraire .
La courbe représentant la fonction x![]() a f
( x) s’obtient à partir de celle représentant x
a f
( x) s’obtient à partir de celle représentant x![]() f (
x) en multipliant les ordonnées des
points par « a ».
f (
x) en multipliant les ordonnées des
points par « a ».
|
INFORMATIONS |
f : R ![]() R
R
x ![]() -
0, 5 x2
-
0, 5 x2
1°)
Ensemble de définition. Df
= R
2°)
Particularité : (est-elle paire ou impaire ? )
quel
que soit le réel « x » appartenant à Df f(-x) = (-x2) = x2 =f(x) ; f est donc « paire » ?,,
3°)
Etude aux bornes du domaine de définition Df:
f)
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x) tend vers -¥ quand « x » tend vers -¥
b) que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f (x) tend vers -¥ quand « x » tend vers +¥
c) que se passe-t-il pour f (x)
quand « x » = 0
f (o) = o
d) résoudre f (x) = o 0 =
- 0,5 x2 donc x
= 0
4°)Sens
de variation :
le
coefficient de x2 est
négatif « a » = -0, 5
f est donc strictement croissante sur R- et strictement décroissante sur R+
5°) le tableau de variation :
|
x |
-¥ 0 +¥ |
|
|
0 - ¥ -¥ |
f admet
un maximum égal à 0 pour x = 0
|
6°) Représentation
graphique : La représentation graphique de la fonction
f s’obtient en multipliant les
ordonnées des points de celle de la fonction x c’
est une parabole d’équation y
= -0,5 x2 , de sommet O (
0 ;0 ) , admettant l’axe (y’ y ) comme axe de symétrie et l’axe
« x’ x » ) comme tangente au sommet . |
|
|
Exemple 3 f :
x |
f :
R ![]() R
R
x ![]() 2x2
2x2
1°)Ensemble
de définition. Df = R
2°)particularité :
(est-elle paire ou impaire ? )
quel
que soit le réel « x » appartenant à Df f(-x) = (-x2) = x2 =f(x) ; f est donc « paire »
3°
) Etude aux bornes du domaine de définition Df:
g)
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x) tend vers +¥ quand « x » tend vers -¥
b) que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f (x) tend vers +¥ quand « x » tend vers +¥
c) que se passe-t-il pour f (x)
quand « x » = 0
f (o) = o
d) résoudre f (x) = o 0 = 2 x2 donc x = 0
4°)Sens
de variation :
le
coefficient de x2 est
positif « a » = 2
f est donc strictement décroissante sur
R- et strictement croissante
sur R+
5°) le tableau de variation :
|
x |
-¥ 0 +¥ |
|
|
+¥
+¥ 0 |
f admet
un minimum égal à 0 pour x = 0
|
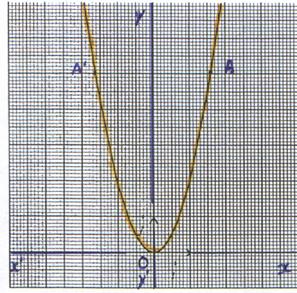
6°) Représentation
graphique : La représentation graphique de la
fonction f s’obtient en multipliant
les ordonnées des points de celle de la fonction x c’
est une parabole d’équation y
= 2 x2 , de sommet O (
0 ;0 ) , admettant l’axe (y’ y ) comme axe de symétrie et l’axe
« x’ x » ) comme tangente au sommet . |
|
|
5- Etude
de la FONCTION MONOME du
troisième degré : f : x |
f :
R ![]() R
R
x![]() x3
x3
1°)Ensemble de définition. Df = R
2°)particularité : (est-elle paire ou
impaire ? )
quel que soit le réel « x » appartenant à
Df
f(-x) = (-x) 3 = -x3 = - f(x) ; f est donc « impaire »
3° ) Etude aux bornes du domaine de
définition Df:
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x)
tend vers - ¥
quand « x » tend vers -¥
que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f
(x) tend vers +¥
quand « x » tend vers +¥
c)
que se passe-t-il pour f (x) quand « x » = 0
f
(o) = o
d)
résoudre f (x) = o 0 = x3 donc x = 0
4°)Sens de
variation :
le coefficient de x3 est positif
« a » = 1
f
est donc strictement décroissante sur R- et strictement croissante sur R+
5°) le
tableau de variation :
|
x |
-¥ 0 +¥ |
|||
|
f(x) |
+¥
0 -¥ |
|
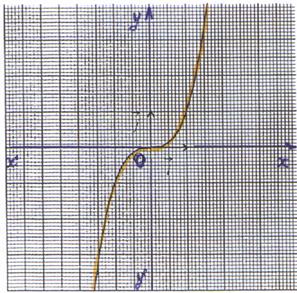
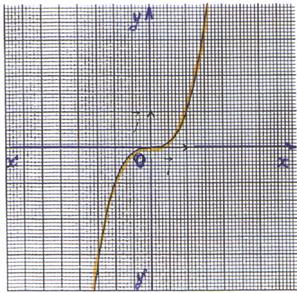
6°) Représentation graphique : La représentation
graphique de la fonction f est la
courbe d’équation y = admettant le
point O (0 ;0 ) comme centre de symétrie et l’axe ( x’x ) comme tangente au point O . |
|
f :
R ![]() R
R
x![]()
![]()
1°)Ensemble de définition.
On ne fait pas la racine carrée d’un
nombre « négatif »
Df
= R+ ou
= [ 0 ; +¥ [
2°)particularité : (est-elle paire ou impaire ?
) pas de réponse !
3° ) Etude aux bornes du domaine de
définition Df:
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
f
(x) tend vers - ¥
quand « x » tend vers -¥ : impossible !
que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f
(x) tend vers +¥
quand « x » tend vers +¥
c)
que se passe-t-il pour f (x) quand « x » = 0
f
(o) = o
d)
résoudre f (x) = o 0 = ![]() donc x = 0
donc x = 0
4°)Sens de
variation :
le coefficient de ![]() 3 est positif
« a » = 1
3 est positif
« a » = 1
f
est strictement croissante sur R+
5°) le
tableau de variation :
|
x |
0
+¥ |
|
|
+¥ 0 |
|
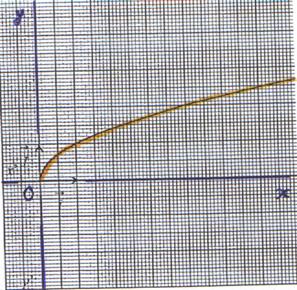
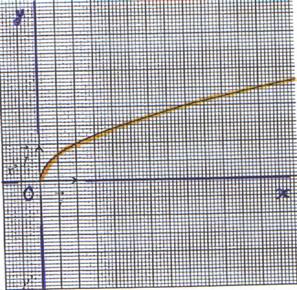
6°) Représentation graphique : La
représentation graphique de la fonction f
est un arc de parabole
d’équation y = |
|
||
7
-ETUDE DE LA FONCTION homographique : f : x |
|
||
f : R ![]() R
R
x ![]()
![]()
1°)
Ensemble de définition.
On
ne peut diviser par 0 donc Df = R* = ]
-¥ ;0[ È ]0 ; +¥ [
2°)
particularité : (est-elle paire ou impaire ? )
quel
que soit le réel « x » appartenant à Df f(-x) = ![]() =
-
=
-![]() = - f(x) ; f est donc « impaire »
= - f(x) ; f est donc « impaire »
3°
) Etude aux bornes du domaine de définition Df:
que se passe-t-il quand f (x)
tend vers 0-
(lire zéro moins)?
f (x) tend vers 0 - quand « x » tend vers -¥
que se passe-t-il pour f (x)
quand « x » tend vers -¥ ?
f (x) tend vers - ¥ quand « x » tend vers 0 -
que se passe-t-il pour f (x)
quand « x » tend vers +¥ ?
f (x) tend vers +¥ quand « x » tend vers 0+
que se passe-t-il quand f (x)
tend vers 0+-
(lire zéro plus)?
f (x) tend vers 0+ quand « x » tend vers +¥
c) que se passe-t-il pour f (x)
quand « x » = 0
f (o) = impossible
d) résoudre f (x) = o 0 = ![]() donc x =
donc x =
4°)
Sens de variation :
le
coefficient de ![]() est positif
« a » = 1
est positif
« a » = 1
f est donc strictement décroissante sur
R- et strictement croissante
sur R+
5°) le tableau de variation :
|
x |
-¥ 0 +¥ |
|
|
0 - +¥ -¥ 0 - |
La double barre indique que
f(x) n’existe pas pour x=0
|
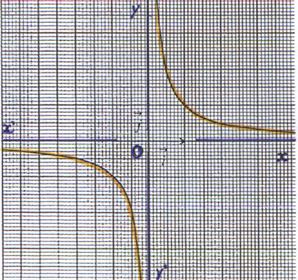
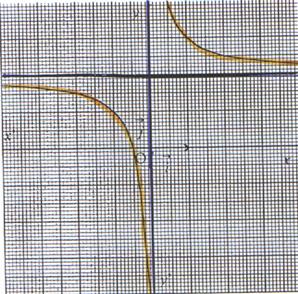
6°)
Représentation graphique :
La représentation graphique de la fonction f est l’ hyperbole d’équation y = |
|
Si f
et g sont deux fonctions définies sur
un intervalle I , on appelle
« somme de deux fonctions » f et g la fonction
notée f + g définie sur l’ intervalle
I par x![]() f(x)
+ g(x).
f(x)
+ g(x).
La
courbe représentant la fonction f + g
est l’ensemble des points de coordonnées ( x ; f(x) + g(x))
Si
f et g sont croissantes ( ou décroissante ) sur I , alors f + g est croissante ou décroissante sur I .
Dans les autres cas , le sens de
variation de f + g se détermine à l’aide de la fonction dérivée de la fonction f + g.
|
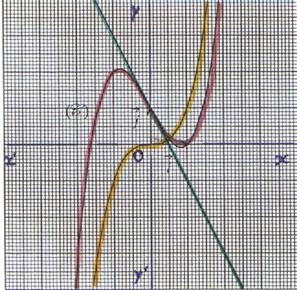
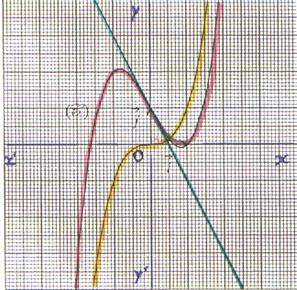
Exemple : Soit les fonctions f et g
de R vers R définies respectivement par f : x La
représentation graphique de f+ g est
la courbe ( C ) . (rouge) |
|
9- Comparaison de deux fonctions :
.
f et g étant deux fonctions
définies sur un intervalle I , dire que f ³ g
sur cet intervalle signifie que pour tout x de I : f(x) ³
g(x)
|
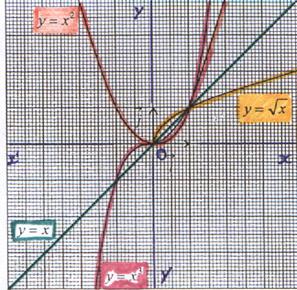
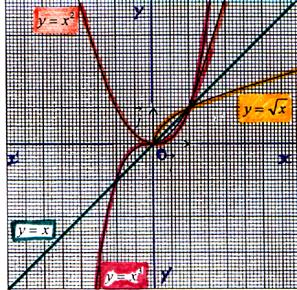
Exemple : soit les fonctions f , g , h , i de R vers R
telles que f : x Sur l’intervalle [
1 ; +¥ [ : i³ h ³ g ³ f |
|
10 - Fonction se déduisant d’une fonction usuelle par addition d’une constante.
Soit b un nombre réel et une
fonction numérique f de R vers R.
Les fonctions x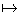 f(x) et x
f(x) et x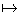 f(x)+b
ont le même sens de variation.
f(x)+b
ont le même sens de variation.
La courbe représentant la fonction x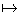 f(x)+b
se déduit de celle représentant x
f(x)+b
se déduit de celle représentant x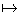 f(x)
par la translation de vecteur b
f(x)
par la translation de vecteur b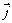
Exemple : f : R ![]() R
R
x![]()
![]() +2
+2
Sens de variation :
f a même sens de variation que x![]()
![]() ;
elle est donc strictement décroissante sur ] -¥ ;0[ et sur ]0 ; +¥ [
;
elle est donc strictement décroissante sur ] -¥ ;0[ et sur ]0 ; +¥ [
le tableau de
variation :
|
x |
-¥ 0 +¥ |
|
|
0 -
+¥
-¥ 0 - |
La double barre indique que f(x) n’existe pas pour x=0
|
6°) Représentation
graphique : La représentation graphique de la fonction f s’obtient à partir de celle de x La représentation
graphique de la fonction f est l’ hyperbole
d’équation y = |
|
TRAVAUX AUTO FORMATIFS.
CONTROLE:
1°)Nommer les étapes qui
concernant l’étude d’une fonction :
CORRIGE :
Etudier une fonction c’est :
A partir de f : R ![]() R
R
x![]() ax
ax
1°) donner l’ensemble de définition.
2°) faire une étude aux b o r n es du domaine de
définition :
a) que se passe-t-il pour
f (x) quand « x » tend
vers -¥ ?
b) que se passe-t-il pour
f (x) quand « x » tend
vers +¥ ?c) que se passe-t-il pour
f (x) quand « x » = 0
d) résoudre f (x) = o
3°)donner le sens de
variation : calculer le taux
d’accroissement
4°) construire le tableau de variation :
type
|
x |
-¥ 0 +¥ |
|
|
? ? ? ? ?sens donner avec des flèches |
5°) faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le
repère cartésien orthonormé ( dit aussi « orthonormal » )
Commentez les
représentations graphiques suivantes :
( forme de
l’équation,Ensemble de définition,particularité : (est-elle paire ou
impaire ? ) Etude aux bornes du domaine de définition, Sens de variation , le tableau de variation .
|
1°) |
|
2°)
|
|
|
|
N°3 |
|
|
N°4 |
|
|
N°5 |
|
|
N°6 |
|
|
N°7 |
|
|
N°8 |
|
|
N°9 |
|
|
N°10 |
|
|
N°11 Commentez les tracés |
|
|
N°12 Commentez :
les tracés |
|