|
|
ENVIRONNEMENT du dossier:
|
|
Objectif
précédent : les
équations (résoudre) |
Tableau |
Liste
des cours et leçons sur LES FONCTIONS et études…. (Sommaire sur…)
Lecture : LES
FONCTIONS ( INFORMATIONS)
De nombreuses données numériques
, c 'est à dire chiffrables , évoluent en fonction d' autres données ,
elles - mêmes chiffrables . Il n 'est pour s ' en convaincre que de se tourner vers
quelques - unes de nos préoccupations habituelles.
Dans la vie quotidienne :
C 'est ainsi que la majorité des hommes
et femmes , soucieux aujourd ' hui de l ' harmonie de
leur silhouette , savent pertinemment que leur poids en kilogramme est fonction
de la quantité de calories consommées au cours des repas quotidiens , mais aussi de leur mode de vie (
actif ou sédentaire )..
De la
même façon , nous savons que la taille et le
poids d ' un enfant évoluent en fonction de son âge . Toutefois
, il n ' existe pas de lien absolu entre âge et taille et poids , car d ' autres éléments non
mesurables interviennent dans le phénomène de croissance ( taille des parents ,
hygiène , niveau de vie , climat ….).
Il est vrai aussi que la pression artérielle
est , chez un être humain , fonction de son âge , de son sexe , mais
encore de sa façon de s 'alimenter ,, de la
quantité de cigarettes fumées et d ' alcool consommé chaque jour , mais
également de son métier et d ' autres facteurs tels que l ' hérédité ou le
tempérament individuel.
Dans
l ' industrie.
Dans un autre domaine , celui de la
construction automobile , il est devenu habituel de présenter comme argument de
vente la consommation d ' essence des voitures proposées , consommation qui
évolue en fonction de la puissance du véhicule , de la vitesse , mais aussi du
style de conduite de chacun et des conditions de circulation ( sur route , en
ville , par temps sec ou humide , etc….. …..)
Le poids des variables
A
travers chacun des exemples précédents , on voit bien qu 'une certaine quantité ( poids , taille , pression
du sang dans les artères , consommation d'essence ) varie en fonction
d' une ou de plusieurs données (
alimentation , âge , mode de vie , vitesse ) que l' on appelle des variables .
En effet , la variation de l 'une
de ces données entraîne immédiatement une variation de la quantité
étudiée .
Pour étudier cette variation , on procède par sondages ou par
mesures successives que l' on regroupe dans un tableau. On peut aussi placer
des points dans un repère .
Pour l '
abscisse , on prendra une valeur de la variable et , pour ordonnée , la valeur
prise par la quantité étudiée pour cette valeur de la variable. On trace
ensuite une courbe passant par ces points. Elle représente la variation de la
quantité en fonction des valeurs prises
par la variable.
Le mot
"fonction" utilisé dans le cours de mathématiques pourra être
plus facilement assimilé si l 'on se réfère aux définitions suivantes que donne le
"Petit Larousse illustré" :
Etre fonction de: dépendre de …
En fonction de ( locution
prépositive) : en suivant les variations de ……
L 'image d ' u n nombre ( si
elle existe) , par une fonction algébrique , est un nombre qui se calcule à l
'aide des quatre opérations usuelles.
CONVENTION DE REPRESENTATION:
Une "patatoïde" représente un ensemble.
Si nous avons deux patatoïdes.
I
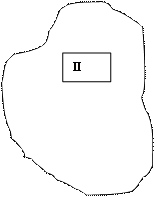
La première ( à
gauche ) représente ce que l' on appelle : l ' ensemble de départ
La deuxième ( à
droite ) représente ce que l ' on appelle : l ' ensemble d ' arrivée
Pour passer de la patatoïde "I" à la patatoïde
"II" : on dit aussi :pour passer de I vers II il faut une relation mathématique notée : Â on dit alors que l' on
construit l' ensemble II à partir
de l ' ensemble I .
La relation mathématique notée : Â est une expression
algébrique contenant une inconnue (généralement des "x") et des
nombres séparés apr des signes opératoires ( addition ,…..)
Généralement ; nous rencontrons les
relations mathématiques du type
suivant:
"3x" ;
"
; donc de la forme "ax"
"3x+5" ; +2 ; …donc de la forme
" ax +b "
3x2 ; 
; …..donc de la
forme "ax2"
3x2+5 ;
+7
; …..donc de la forme
"ax2+b"
3x2+5x
; +7x
; …..donc de la forme
"ax2+bx"
3x2+5x +1 ; +7x+2
; …..donc de la forme
"ax2+bx+c"
D'autres sont du genre:
; 
;……………
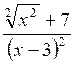Ces relations mathématiques se
mettrons sous la forme d 'une équation qui commencera
toujours sous la forme " y
=……" tel que
Avant de continuer vous devez faire le devoir :
cliquez
ici
|
DEVOIR de CALCUL dit "algébrique" de premier
degré |
|
|
|
|
|
Soit x élément de l'
ensemble de départ ( I ) |
Soit la relation mathématique: |
Alors l 'élément dans l 'ensemble d' arrivée ( II ) prendra
pour valeur: |
|
équation |
Si x = 2 |
Alors y = |
|
|
|
|
Y = 3x |
|
|
X vaut 2 |
3x |
Alors y vaut 6 |
|
Y = |
|
|
|
|
|
|
Y =3x+5" ; |
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
Y =3x2; |
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
Y =3x2+5x
; |
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
Y =3x2+5x +1 |
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
Y = |
|
|
|
|
|
Ce module à pour but d’aborder tout ce
qui touche à la fonction en général.
Ce module est composé de six objectifs
et une fiche « récapitulatif »
Lorsque ce module sera entièrement
maîtrisé vous pourrez ,voir ou revoir le module
traitant des rapports ,proportions et grandeurs proportionnelles ;et
aborder la fonction linéaire.
Info. quand la fonction linéaire est
maîtriser vous pourrez aborder les applications
sur la fonction linéaire , à savoir :
1.
les pourcentages
2.
Echelle
3.
les relations trigonométriques