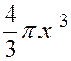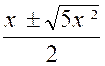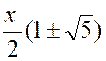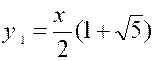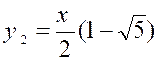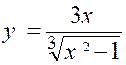Les modes de représentations mathématiques
![]()
![]()

![]()

![]()

![]()

![]()
![]()
![]() d’une situation
d’une situation
ENVIRONNEMENT du dossier:
|
Objectif précédent |
Objectif suivant : 1°) Etude sur l’étude de la représentation graphique d’une
fonction |
1°) Les
fonctions niveau V B EP . 2°) Le
second degré niveau V BEP 3°) Les tracés BEP |
Généralités
sur LES FONCTIONS : « nomenclature » et « ses MODES DE
REPRESENTATION »
|
Chapitres : |
|
|
|
|
||
|
|
· Variables et
constantes. |
|
|
|
· Fonction d’une
variable. |
|
|
|
· Les fonction algébriques et transcendantes. |
|
|
|
· Fonctions de
plusieurs variables ; |
|
|
Partie II ) Les
différents modes de représentation d’une fonction.. |
|
|
|
|
III ) voir les études d’une fonction.. |
|
|
|
|
|
|
Partie I ) Les fonctions « nomenclature ». |
|
|||||
|
|
« variables et constantes » |
|
||||
|
|
On dit qu’une quantité est « variable »
quand elle est susceptible de passer par différentes valeurs ; Par opposition , on dit
qu’une quantité est « constante » lorsque sa valeur est fixe. On désigne généralement les variables par les
dernières lettres de l’ alphabet
« x » ; « y » ; « z » ;
« t » ; « u » ; « v » ;
« w » ;… ;et les constantes par les premières
lettres « a » ;
« b » ; «c » ;…. |
|
||||
|
|
« Fonctions d’une variable ». |
|
||||
|
|
On dit qu’une quantité variable « y » est
fonction d’une autre quantité variable « x » quand « y »
dépend de « x » suivant une loi connue ,
de telle manière qu’à chaque valeur attribuée à « x » corresponde
une valeur bien déterminée de « y ». La quantité « x » qu’on peut faire
varier d’une manière arbitraire porte le nom de « variable
indépendante ». Une fonction « y » de la variable
« x » est définie au point de vue mathématique ,
dès qu’on se donne la relation qui permet de calculer « y » quand
on connaît « x ». |
|
||||
|
|
Exemple 1 : la longueur « y » de la circonférence , le volume
« z » d’une sphère sont des fonctions de leur rayon « x »
définies par les relations : |
|
||||
|
|
|
« y = 2 |
|
« z
= |
|
|
|
|
Le sinus « y » d’un angle
« x » est une fonction de cet angle : « y = sin . x » |
|
||||
|
|
|
|
||||
|
|
Exemple 2 : Soit l’équation : «
y² - xy – x²
= 0 » A toute valeur de « x » , elle fait correspondre deux valeurs de « y »
que l’on obtient en résolvant . « y = Ces deux fonctions : S’appellent des « fonctions implicites » parce qu’elles sont définies par une
équation non résolue par rapport à « y ». Au contraire, les fonctions définies par une
équation de la forme :
« y = f (x ) »
qui est résolue par rapport à « y » sont dites « fonctions explicites ». Dans
certain cas , il n’est pas possible
« d’expliciter » une équation, c'est-à-dire de la résoudre par
rapport à « y » en fonction
de « x ». Ce serait le cas de l’équation : « y² - xy – 1 = 0 » D’une manière générale une relation quelconque
qui lie la fonction « y » ou « z » à la variable
« x » dont elle dépend , peut se
représenter par l’une des notations : |
|
||||
|
|
|
« y = f ( x ) » |
« y = F ( x ) » |
« z = |
|
|
|
|
Pour désigner la valeur numérique que prend une
fonction « f ( x ) »lorsqu’on donne à la
variable une valeur particulière , on remplace à l’intérieur des parenthèses
« x » par cette valeur. Ainsi
« f ( 0 ) » ; « f ( 1 ) » ; « f
( -2 ) » désignent les valeurs
numériques de « f ( x ) » pour « x = 0 » ; «
x = 1 » ; « x = ( - 2)
» |
|
||||
|
|
|
|
||||
|
|
« Fonction algébriques » et « fonctions transcendantes. » |
|
||||
|
|
On distingue parmi les fonctions
, les « fonctions algébriques » et les « fonctions
transcendantes ». |
|
||||
|
|
Les fonctions algébriques sont celles où
l’équation qui lie la fonction à la variable ne renferme qu’un nombre limité
d’opérations de l’algèbre élémentaire : addition ; soustraction, multiplication , division , fraction , élévation à une
puissance constante , ou extraction de racine déterminée.
|
|
||||
|
|
|
|
||||
|
|
Exemples de fonctions algébriques : |
|
||||
|
|
« y = 2 x² - 5 x + 4 » ; |
|
||||
|
|
|
|
||||
|
|
Exemples de fonctions transcendantes : « y = sin x »
; « y = log
x » |
|
||||
|
|
|
|
||||
|
|
Fonctions de plusieurs variables
. |
|
||||
|
|
On dit qu’une quantité variable « z »
est fonction de deux autres quantités variables « x » et
« y » , quand « z » dépend de
« x » et de « y » suivant une loi connue , de telle
manière qu’à chaque système de valeurs attribuées à « x » et à
« y » corresponde une valeur bien déterminée de « x ». Les quantités « x » et « y »
auxquelles on peut donner des valeurs arbitraires et indépendantes l’une de
l’autre sont appelées « variables indépendantes ». Une fonction « z » de deux variables
« x » et « y » est définie au point de vue mathématique
lorsqu’on donne une relation permettant de calculer « z » quand on
connaît « x » et « y ». |
|
||||
|
|
Exemple : L’aire « z » d’un
rectangle est une fonction de ses deux dimensions « x » et
« y » définie par la relation : « z = x y » On rencontre également des fonctions de trois variables , de quatre variables , …… Lorsqu’ on ne voudra pas préciser la nature de la
fonction, on représentera une fonction « z » de deux variables
« x » et « y » , une fonction « y » de trois variables « u ;
v ; w » , par des notations de ce genre : « z =
f ( x ; y ) » ;
« y = f ( u ;
v ; w ) » Une fonction de plusieurs variables peut être algébrique ou
transcendante. |
|
||||
|
|
Résumé : On dit
qu’une variable « y » est fonction d’une autre variable
« x » , si l’on peut calculer « y » lorsqu’on se donne
la valeur de « x ». On distingue les fonction algébriques
, dont la définition ne fait intervenir que les opérations de l’algèbre
, et les fonctions transcendantes qui , par définition , ne sont pas
algébriques. Il peut se faire qu’une variable « z »
soit à la fois fonction de plusieurs variables telles que « z » et
« y ». |
|
||||
|
|
|
|
||||
|
Partie 2 : Les 4 différents modes de
représentation d’une fonction. |
|
|||||
|
|
|
|
||||
|
Pour tous les élèves qui doivent
étudier les fonction en milieu scolaire : IMPORTANT à lire et s’imprégner
: A voir : cliquez ici : « Fonction et
application » :
( définitions) |
INFORMATIONS : Ce dossier traite des généralités
sur la fonction
Une fonction peut
s’identifier à partir de quatre modes de représentation :
|
|
|
|
|
Liste des différents modes de
représentation d’une fonction |
Pré requis : |
Cliquez
sur la pastille : |
|
|
|
|
|
I ) Equation |
||
|
|
|
|
|
II ) Graphe |
||
|
|
|
|
|
III ) Tableau
de variation |
Pré
requis :le tableau à double entrées
|
|
|
|
|
|
|
IV ) Représentation graphique. |
Travaux proposés :
|
Tests « évaluations » : |
|
|
Tests contrôle des savoirs |
|
|
Devoir
sommatif |
Consigne :
Vous cliquez sur un point pour
obtenir un des chapitres