Pré requis:

Les Fonctions USUELLES
Savoir Tracer une courbe dans un repère .

ENVIRONNEMENT du dossier:

Index

Objectif précédent   Algèbre : le second degré. A lire : 1°) étude graphique d’une fonction. 2°) Etude d’une fonction (application de la dérivée)

Objectif suivant 1°) Le second degré au niveau I V. 2°° Suite : fonction x² 3°) la parabole .

Info :  Etude de la fonction trinôme du second degré.

DOSSIER :

ETUDES DES FONCTIONS USUELLES du Second  Degré (forme y = a x²)

Et la fonction monôme du troisième degré.(forme : y = x ³ )

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

COURS

 

FONCTION MONOME du second degré :                 f : xax2

INFORMATIONS

 

Etudier une fonction  du second degré c’est :

 

Exemple 1  

   ²

1°) Ensemble de définition.  

 

2°)  Particularité : (est-elle paire ou impaire ? )

quel que soit le réel « x » appartenant à Df   f(-x) = (-x²) = x²  =f(x) ; f est donc « paire ».

 

3° ) Etude aux bornes du domaine de définition Df:

 

a)  Q ue se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

f (x) tend vers +¥  quand « x » tend vers -¥ 

b) que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?

f (x) tend vers -¥  quand « x » tend vers -¥ 

c) que se passe-t-il pour  f (x)  quand « x » = 0

f (o) = o

d) résoudre  f (x) = o    0 =  x²         donc x = 0

 

4°) Sens de  variation :

 

 voir le calcul  du  taux correspond  à « a »

f est donc strictement décroissante sur R^-  et strictement croissante sur R⁺

 

5°)  Le tableau de variation :

 

x	-¥                                0                                           +¥
f(x)	+¥                                                                         +¥                                               0

                                

 

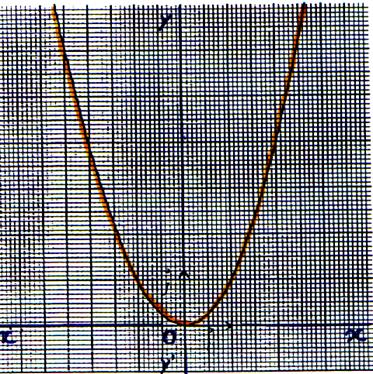
6°) Représentation graphique : La représentation graphique de la fonction f est une parabole  d’équation 2 , de sommet  O ( 0 ;0 ) , admettant l’axe (  ) comme axe de symétrie et l’axe « » ) comme tangente au sommet .

Fonction se déduisant d’une fonction usuelle par multiplication par une constante .

 

Soit « a » un nombre réel et une fonction numérique de R vers R.

 

-       si a > 0  , les  fonctions    f ( x) et    a f ( x)  ont le même sens de variation.

 

-       si a < 0  , les  fonctions    f ( x) et    a f ( x) varient en sens contraire .

 

La courbe représentant la fonction   a f ( x) s’obtient à partir de celle représentant    f ( x)   en multipliant les ordonnées des points par « a ».

 

 

 

FONCTION MONOME du second degré : f :  2

INFORMATIONS

 

Exemple 2                      

 - 0, 5 x²

 

1°) Ensemble de définition.   Df  =  R

 

2°)  Particularité : (est-elle paire ou impaire ? )

quel que soit le réel « x » appartenant à Df   f(-x) = (-x²) = x²  =f(x) ; f est donc « paire » ?,,

 

3° ) Etude aux bornes du domaine de définition Df:

b)  que se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

f (x) tend vers -¥  quand « x » tend vers -¥

b) que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?

f (x) tend vers -¥  quand « x » tend vers +¥

c) que se passe-t-il pour  f (x)  quand « x » = 0

f (o) = o

c)   résoudre  f (x) = o

 

0 =  - 0,5 x²         donc x = 0

 

4°) Sens de  variation :

 le coefficient de x²  est négatif   « a » = -0, 5

f est donc strictement croissante sur R^-  et strictement décroissante sur R⁺

 

5°)  Le tableau de variation :

 

x	-¥                                      0                                     +¥
f(x)	0         - ¥                                                                            -¥

                                   f   admet un maximum égal à 0 pour x = 0

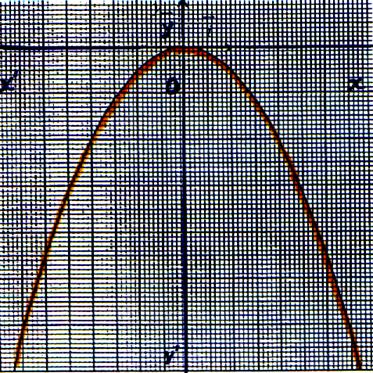
6°) Représentation graphique : La représentation graphique de la fonction f  s’obtient en multipliant les ordonnées des points de celle de la fonction                    x2  par –0,5   c’ est une parabole  d’équation y = -0,5 x2 , de sommet  O ( 0 ;0 ) , admettant l’axe (y’ y ) comme axe de symétrie et l’axe « x’ x » ) comme tangente au sommet .
FONCTION MONOME du second degré : f :   ax2		INFORMATIONS

Exemple 3                               

f   : R  R

  2x²

1°)  Ensemble de définition.   Df  =  R

 

2°)  Particularité : (est-elle paire ou impaire ? )

quel que soit le réel « x » appartenant à Df   f(-x) = (-x²) = x²  =f(x) ; f est donc « paire »

 

3° ) Etude aux bornes du domaine de définition Df:

 

a) que se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

f (x) tend vers +¥  quand « x » tend vers -¥ 

b) que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?

f (x) tend vers +¥  quand « x » tend vers +¥ 

c) que se passe-t-il pour  f (x)  quand « x » = 0

f (o) = o

d) résoudre  f (x) = o    0 = 2 x²         donc x = 0

 

4°) Sens de  variation :

 le coefficient de x²  est positif   « a » = 2

f est donc strictement décroissante sur R^-  et strictement croissante sur R⁺

 

5°)  Tableau de variation :

 

x	-¥                                    0                                       +¥
f(x)	+¥                                                                            +¥                                               0

                                   f   admet un minimum égal à 0 pour x = 0

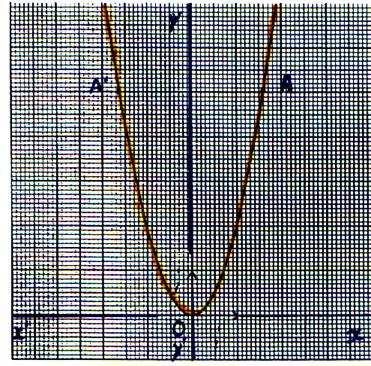
6 °) Représentation graphique : La représentation graphique de la fonction f  s’obtient en multipliant les ordonnées des points de celle de la fonction x x2  par 2   c’ est une parabole  d’équation y = 2 x2 , de sommet  O ( 0 ;0 ) , admettant l’axe (y’ y ) comme axe de symétrie et l’axe « x’ x » ) comme tangente au sommet .

 

 

FONCTION MONOME du troisième  degré :    f : ax3

INFORMATIONS

f : R  R

x ³

1°) Ensemble de définition.   Df  =  R

 

2°)  Particularité : (est-elle paire ou impaire ? )

quel que soit le réel « x » appartenant à Df   f(-x) = (-x) ³ = -x³  = - f(x) ; f est donc « impaire »

 

3° )  Etude aux bornes du domaine de définition Df:

que se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

f (x) tend vers - ¥  quand « x » tend vers -¥

 que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?

f (x) tend vers +¥  quand « x » tend vers +¥

c) que se passe-t-il pour  f (x)  quand « x » = 0

f (o) = o

d)  résoudre  f (x) = o   

0 =  x³         donc x = 0

 

4°) Sens de  variation :

 le coefficient de x³  est positif   « a » = 1

f est donc strictement décroissante sur R^-  et strictement croissante sur R⁺

5°)  le tableau de variation :

 

x	-¥                                    0                                        +¥
f(x)	+¥                                       0  -¥

 

 

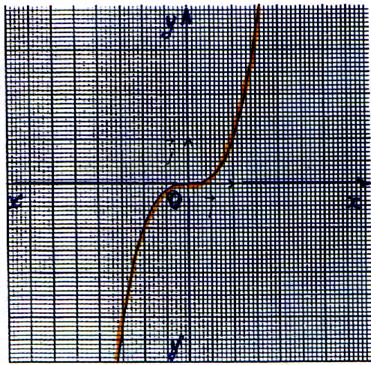
6°) Représentation graphique : La représentation graphique de la fonction f  est la courbe d’équation y =     admettant le point O (0 ;0 ) comme centre de symétrie et  l’axe ( x’x )  comme tangente au point O .

 

TRAVAUX   AUTOFORMATIFS

CONTROLE:

 

Question :   Donner les étapes d’étude d’une fonction :

 

 

 

EVALUATION:

 

1°)  Faire l’étude de la fonction :

f :   R  R x         x2

2°)  Faire l’étude de la fonction :

f    :  R  R x      - 0, 5 x2

3°)  Faire l’étude de la fonction :

f   : R  R x        2x2

4°)  Faire l’étude de la fonction :

f :     R  R x      x3

 

 

 

 

 

 

Corrigé :

Voirs dans le cours :

Question :   Donner les étapes d’étude d’une fonction :

 

Etudier une fonction c’est :

 

 

A partir de                               f : R  R

x      ax

1°)donner l’ensemble de définition.

 

2°)faire une étude aux bornes du domaine de définition :

a) que se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

b) que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?c) que se passe-t-il pour  f (x)  quand « x » = 0

d) résoudre  f (x) = o 

 

3°)donner le sens de  variation : calculer le taux d’accroissement

 

 

 

4°) construire le tableau de variation :

 

type

x	-¥                                0                                              +¥
f(x)	? ? ? ? ?sens donner avec des flèches

 

5°) faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )