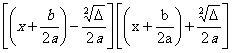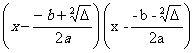DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

DOSSIER N° 3 sur le Second degré. Matière : MATHEMATIQUE :

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

Formation : NIVEAU  IV : BAC PROFESSIONNEL : Formation Niveau IV

OBJECTIFS : - Savoir résoudre l’équation du second degré : «  a x² + b x + c = 0 »   - Savoir factoriser le polynôme de la forme : « a x² + b x + c » En vu d’étudier les fonctions de la forme : f(x) = a x² + b x + c ayant pour équation : y = a x + b x +c .

I ) Pré requis:

1-	Cours de niveau V (repérage) BEP - CAP
2-	Pré requis tracés géométriques	:i
3-	Cours niveau V sur la fonction (en BEP)	:i
4 -	TESTS : Calculs ( série E , et toute la partie 2)	:i
5-	TESTS : tracés (série 1 : n°6 et série 2 : n°5)	:i
6 -	INFO : Représentation graphique d’une fonction	:i

II ) ENVIRONNEMENT du dossier :

Index warmaths

Dossier précédent : 1°)Fonction « a x² » 2°) :voir résolutions des équations du second degré incomplètesi 3°) Résumé niv V / niv IV.

Dossier suivant : - Somme et produit. - Niveau IV dossier 4 - Les fonctions(étude) de la forme : y = a x² + b x + c - Résoudre un système d’équation du second degré.

Info : Tableau synoptique :i Info : Retour vers la liste des cours sur le second degré « équations »

III ) LECON n°3 : LE SECOND DEGRE (niv IV / niv. III )

Chapitres :

i9	Définition	:i
iles IR9	Résoudre l’équation de la forme a x² + bx + c = 0	:i
		et - Somme et produit.
i19	Factorisation de «  a x² + b x + c » démonstration  exemple et cas général	Forme canonique :i
i29		2°) Factoriser :
i9	Système d’équations comportant le produit de deux inconnues ou leur carré.	:i
	Racines et signe du trinôme
i9	Inéquation du second degré (signe du trinôme et résolution à partir d’un tableau.	:i

IV) INFORMATIONS «  formation leçon » :

Test	COURS	Travaux auto - formation.		Ici : Exercices corrigés	Corrigé des travaux auto - formation.
		Contrôle	évaluation	Interdisciplinarité  Débouche sur ! résoudre une situation problème du second degré	Corrigé Contrôle	Corrigé évaluation

V ) DEVOIRS ( écrits):

Devoir diagnostique L tests. (devoir 1)	Ÿ
Devoir Auto - formatif (intégré au cours)  ici : ; autres devoirs à préparer	Ÿ
Devoir Formatif « Contrôle : savoir » ; (remédiation)	Ÿ
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	Ÿ
Devoir sommatif.	Ÿ
Devoir certificatif : (remédiation)	Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°3	LE SECOND DEGRE

CHAPITRES

i9	Définition	:i
i9	Résoudre l’équation de la forme a x² + b c + c = 0	:i
i9	Factorisation Démonstration	:i
i9	Système d’équations comportant le produit de deux inconnues ou leur carré.	:i
	Racines et signe du trinôme
i9	Inéquation du second degré.	:i

COURS

i9

Définition

:i

Une équation du second degré d’inconnue « x » est une équation de la forme :

a x² + b x + c = 0

« a », « b », « c » sont les coefficients ( ce sont des nombres réels) ; et « a » "` 0

info : a x² + b x + c = 0 est un trinôme de degré deux , appelé « polynôme du second degré ».

Activité : x² + 2 x = -1 se ramène à la forme x² + x - 1 = 0

3 x² = + 2x - 5 se ramène à la forme 3x² - 2 x + 5 = 0

x² = 9 x - 6 se ramène à la forme x² - 9 x + 6 = 0

i9

Résoudre l’équation de la forme a x² + b c + c = 0

:i

	a x² + b c + c = 0
	Calcul du discriminant : ∆ = b² - 4 ac
∆ > 0		∆ = 0	∆ < 0
Deux solutions : x’ = x’’ =		Une solution : x’ = x’’ =	Aucune solution

Remarques :

la première solution se note , invariablement , : x’ (lire : ixe prime) ou x₁ ( lire : ixe indice 1)

la deuxième solution se note , invariablement , : x’’ (lire ixe seconde) ou x₂ ( lire :ixe indice 2)

EXEMPLES DE RESOLUTION : (parfois Il faut transformer l’égalité et ramener l’équation à la forme d’un polynôme du second degré ( vu précédemment) )

Exemple 1 : résoudre x² - 9 x + 6 = 0

Procédure :	x² - 9 x + 6 = 0 ; x’ = ? et x’’ = ?
Identifions les coefficients	a = 1 ; b = -9 ; c = 6
Calcul du discriminant : ∆ = b² - 4 ac	(-9) ² - 4 × 1 × 6 ; = 81 - 24 ; = 57
Analyse du signe et du résultat de ” 1^ère conclusion :	Le discriminant est > 0 ; positif Le discriminant étant positif l’équation a …2…solution (s)
Calcul de la racine de ” ( )	# 7,55
Calcul de la ou des solutions :	x1 = = 8,275 x2 = =0,725
2^ème conclusion :	x² - 9 x + 6 = 0 à pour solutions (racines) 8,275 et 0,725

Activité : résoudre 7 x² + 5 x - 38 = 0 ( x’ = 2 ; x’’ = )

Exemple 2 : résoudre 25 x² - 30 x + 9 = 0

Identifions les coefficients	a = 25 ; b = - 30 ; c = 9
Calcul du discriminant ∆ = b² - 4 ac	( - 30)² - 4 × 25 × 9 ; 900 - 900 = 0
Analyse du signe et du résultat de ” 1^ère conclusion :	Le discriminant est nul (= 0) L’équation a 2 solution (s) égales.
Calcul de la racine « double »
Calcul de la ou des solutions :	x ‘ = x ‘’ = = = 0,6
2^ème conclusion :	25 x² - 30 x + 9 = 0 à pour solutions x ‘ = x ‘’ = 0,6

Exemple 3 : résoudre 2 x² - 4 x + 5 = 0

Identifions les coefficients	a = 2 ; b = - 4 ; c = 5
Calcul du discriminant ” = b² - 4 ac	( - 4)² - 4 × 2 × 5 = 16 - 40 = -30
Analyse du signe et du résultat de ” 1^ère conclusion :	Le discriminant est négatif L’équation n’admet pas de solution

i9	FACTORISATION : Démonstration sur la factorisation du polynôme a x² + b x + c	1°) Forme canonique :i 2°) Factoriser :
	Ici : Activité pédagogique

Pour factoriser il faut connaître les racines de l’équation !donc avant de factoriser il faut « résoudre ».

Application numérique	Cas général
Résoudre l’équation x² - 4 x + 3 = 0	Résolution de l’équation a x² + b x + c =0  Le coefficient « a » ¹ 0
Factorisons le polynôme : - 4 x = - 2 × 2 × x x² - 4 x sont les 2 premiers termes du développement * de (x - 2)²	On met en facteur « a » a x² + b x + c = a ( x² + x +) On factorise x² + x + (1)
*Le développement de l’I.R. (x - 2)² étant : x² - 4 x + 4	Ainsi on sait que : (x + ) ² = x² + x +
Nous pouvons établir l’égalité : x² - 4 x + 3 = x² - 4 x + 4 - 4 + 3	Par conséquent : x² +x + = x ² + x+ - +
Ainsi : x² - 4 x + 3 = (x - 2)² + 1 comme 1 = 1² = 1×1 = 1 ; on peut écrire (x - 2)² + 1 = (x - 2)² + 1² On remarque que X² + 1² = (X+1) (X-1)	Voir l’identité remarquable de la forme a ² - b² = ( a + b ) ( a - b) regroupons + Û
D ‘ où : (x - 2)² + 1² = [ ( x -2) +1) ( x - 2 - 1) ]	L’équation (1) devient ( x + )² - +=( x + )² - (2)
(x - 2)² + 1² = ( x -1) ( x - 3)	Soit : ” le discriminant On pose : ∆= b² - 4 ac

L’expression factorisée de x² - 4 x + 3 est : ( x -1) ( x - 3)

On discute suivant la valeur de ” pour obtenir une factorisation possible: Si ∆ > 0 : l’expression (2) s’écrit : = les racines du polynôme a x² + b x + c sont x’ =  ; x’’ = On peut écrire : = ( x - x’ ) ( x - x’’) Si ∆ = 0 ; l’expression (2) s’écrit : ( x + )² - = ( x + )² - ” = ( x + )² - 0 = ( x + )² La racine du polynôme « a x² + b x + c » est x’ (= x’’) = On peut écrire : ( x - x’ )² (ou) ( x - x’’)² Si ∆ < 0 : le polynôme « a x² + b x + c » ne peut être factorisé et il n’a donc pas de « racine »

Résolution de l’équation : Pour que ( x -1) ( x - 3) = 0 Il faut que (x -1) = Soit : x - 1 = 0 Û x = 1 0 et ou (x - 3) =0 x - 3 = 0 Û x = 3

FACTORISATION (résumé)

	Cas général : a x² + b x + c	Application : « factoriser »
1^er cas : ∆ > 0	Alors 2 racines : x ‘ et x ’’ Factorisation : a x² + b x + c = a ( x -x’) ( x -x’’)	7 x² + 5 x - 38 = 0 les racines sont x’ = 2 ; x’’ = Factorisation : = 7 ( x - 2 ) ( x - ) vérification : il faut développer.
2^e cas ∆ = 0	Alors 1 racine : x ‘ (ou) x ’’ Factorisation : a x² + b x + c = a( x -x’)² (ou) a( x -x’’)²	25 x² - 30 x + 9 = 0 une racine « double » : 0,6 Factorisation : = 25 ( x - ² vérification : il faut développer.
3^e cas ∆ < 0	Pas de racine ; la factorisation n’est pas possible.	2 x² - 4 x + 5 = 0 ∆ = - 30 Pas de factorisation possible

On retiendra la procédure suivante:

Pour factoriser un polynôme de la forme a x² + b x + c il faut résoudre l’équation a x² + b x + c = 0 .

Il faut appliquer la procédure suivante :

- calculer le discriminant. ∆= b² - 4 ac

- ensuite il suffit d’appliquer  suivant la valeur de ”:

Si : ∆ > 0	Alors 2 racines : x’ =  ; x’’ = Factorisation : a x² + b x + c = a ( x -x’) ( x -x’’)
Si ∆ = 0	Alors 1 racine : x ‘ (ou) x ’’ = Factorisation : a x² + b x + c = a( x -x’)² (ou) a( x -x’’)²
Si ∆ < 0	Pas de racine : On rédige la phrase : La factorisation n’est pas possible puisque le discriminant est négatif. ( = …)

i9

Système d’équations comportant le produit de deux inconnues ou leur carré.

:i

Voir les INFORMATIONS SUR la somme ( S ) et le produit ( P ) des solutions :

Le système est de la forme

Pour résoudre un système de deux équations faisant intervenir leur produit ou leur carré , on peut utiliser :

- Soit la méthode de substitution.

- Soit résoudre l’équation de la forme x² - S x + P = 0

Exemple : résoudre le système

Par substitution :	Par x² - S x + P (1)
de l’équation (1) tirons y = 9 - x (3) On remplace (3) dans (2) x ( 10 - x ) = 20 on développe : 9x - x² = 20 on transforme l’équation pour ……= 0 0 = 20 - 9 x + x² On résout l’équation x² - 9 x + 20 = 0 a = 1 ; b = -9 ; c = 20 Calcul de ” = 81² - 4 fois 20 = 81 - 80 = 1 Calcul de = x’ = 4 et x’’ = 5 conclusion les deux nombres sont 4 et 5	On note que S = x+y = 9 On note que P = x y = 20 On remplace dans l’équation (1) : x² - 9 x + 20 = 0 IL suffit de résoudre l’équation : On trouve x’ = 4 et x’’ = 5 Les deux nombres ont pour valeur : 4 et 5 Conclusion
Les nombres dont la somme est « 9 » et le produit « 20 » sont 4 et 5

(pas de système à résoudre)

Activité : résoudre le système (sol. : 2 et 3)

i29

« Racines » et « signe » du trinôme.

:i

Commentaire : nous devons faire l’étude d’une fonction de la forme y = a x² + b x +c .

Lors de cette étude il est demandé de savoir donner le signe du trinôme « a x² + b x + c » lors que l’on fait varier « x ».

La valeur de « x » peut être positif, négatif ou être égal à « 0 ».

On se pose la question : Quel est le signe du résultat du calcul du trinôme si l’on prend « x » >0 ; < 0 ou = 0 ?

ACTIVITES :

Activité 1 :

A ) remplir le tableau :

x	- 20	-15	-10	-7	-5	+0	+2	+3	+5	+10	+20
x² + 2x - 15

B ) Avec un logiciel traceur de courbe sortir le graphique y = x² + 2x - 15

Activité 2 :

A ) remplir le tableau :

x	- 20	-15	-10	-7	-4	-3	-2	+3	+5	+10	+20
-x² - 9x - 14

B) Avec un logiciel traceur de courbe sortir le graphique y = -x² - 9x - 14

Activité 3 :

A) remplir le tableau :

x	- 20	-15	-10	-5	-3	+0	+2	+3	+5	+10	+20
3x² - 2x + 14

B) Avec un logiciel traceur de courbe sortir le graphique y = 3x² - 2x + 14

Activité 4 :

A ) remplir le tableau :

x	- 20	-10	-5	-3	0	+2	+3	+6	+7	+10	+20
x² - 12x +36

B) Avec un logiciel traceur de courbe sortir le graphique y = x² - 12x +36

Recherche du signe du trinôme a x² + b x + c

Il faut tout d’abord résoudre l’équation a x² + b x + c = 0 ; de là trois cas peuvent se présenter. (suivant la valeur de ”)

I ) Cas où le ∆ est supérieur à 0 (∆ > 0)

Premier exemple : Soit le trinôme x² + 2x - 15

On remarque que : a = + 1 > 0 ; Les racines du trinôme sont x₁ = -5 ; x ₂ = +3

Activité 1 :

A ) remplir le tableau :

x	- 20	-15	-10	-7	-5	+0	+2	+3	+5	+10	+20
x² + 2x - 15					0			0
Signe du résultat du calcul du trinôme :	+	+	+	+		-	-		+	+	+
Noter : Signe de « a » ou signe de « -a »	a	a	a	a		-a	-a		a	a	a

B ) Avec un logiciel traceur de courbe sortir le graphique y = x² + 2x - 15 , comparer les calculs et la courbe.

Si l’on trace la courbe : y = x² + 2x - 15 (activité 1-B)

Etude du signe de  x² + 2x - 15, d’après le tableau.	Forme du graphique : vérifiez !
Si x < -5 ; x² + 2x - 15 > 0 Si x = -5 ; x² + 2x - 15 = 0 Si x > 3 ; x² + 2x - 15 > 0 Si x = 3 ; x² + 2x - 15 = 0 Si - 5 < x > 3 ; x² + 2x - 15 < 0

Ces résultats peuvent être consignés dans un tableau des signes :

x		-5		+3
Signe de x² + 2x - 15
	+	0	-	0	+

Conclusion :

Le coefficient « a » du trinôme x² + 2x - 15 > 0 à pour valeur a = +1 > 0.

Le trinôme a le signe de « a » pour les valeurs de « x » extérieures à -5 et à + 3

Le trinôme a le signe contraire de « a » pour les valeurs - 5 <  x  < +3

Soit l’inégalité x² + 2x - 15 > 0

L’inégalité proposée est donc vérifiée pour x < -5 et x > 3

Soit l’inégalité x² + 2x - 15 < 0

L’inégalité proposée est donc vérifiée pour - 5 <  x  < +3

Deuxième exemple : Soit le trinôme = - x² - 9x - 14

Activité 2 :

A ) remplir le tableau :

x	- 20	-15	-10	-7	-4	-3	-2	+3	+5	+10	+20
-x² - 2x - 14
Signe du résultat du calcul du trinôme :	-	-	-		+	+			-	-	-
Noter : Signe de « a » ou signe de « -a »	a	a	a		-a	-a		a	a	a	a

B) Avec un logiciel traceur de courbe sortir le graphique y = - x² - 9x - 14

Les racines du trinôme sont x₁ = -7 ; x ₂ = -2

Si l’on trace la courbe : y =- x² - 9x - 14 (activité 1-B)

Etude du signe de  x² + 2x - 15	Forme du graphique
Si x < - 7 ; - x² - 9x - 14 < 0 Si x = -7 ; - x² - 9x - 14 = 0 Si x > -2 ; - x² - 9x - 14 < 0 Si x = -2 ; - x² - 9x - 14 = 0 Si - 7 < x > -2  ; x² - 9x - 14 > 0

Ces résultats peuvent être consignés dans un tableau des signes :

x		-7		-2
Signe de -x² - 9x - 14
	-	0	+	0	-

Conclusion :

Le trinôme - x² - 9x - 14 > 0 ; a = -1 < 0.

Le trinôme a le signe de « a » pour les valeurs de « x » extérieures à -7 et à - 2

Le trinôme a le signe contraire de « a » pour les valeurs -7 < x < -2

Soit L’inégalité : - x² - 9x - 14 > 0 

L’inégalité proposée est donc vérifiée pour -7 < x < -2

Soit L’inégalité : - x² - 9x - 14 < 0 

L’inégalité proposée est donc vérifiée pour x < -7 et x > -2

En résumé :

Si ∆ > 0 ; le trinôme à deux racines

Si « a » > 0

x		-5		+3
Signe de x² + 2x - 15
	+	0	-	0	+

Et si a < 0

x		-7		-2
Signe de -x² - 9x - 14
	-	0	+	0	-

On peut observer que le signe du trinôme a x² + b x + c dépend du signe de « a »

Si ∆ > 0 ; le trinôme à deux racines :

x		x1			x 2
Signe de a x² +b x + c
	Signe de « a »		0	Signe de « - a »	0	Signe de « a »

II ) Cas où le ∆ est inférieur à 0 (∆ < 0)

Voir l’activité :

Voir le trinôme 3x² - 2x + 14 

Calcul du discriminant du trinôme : 3x² - 2x + 14 ; ” = (-2 )² - 4 fois 3 fois 14 = 4 - 168 = -164

A ) remplir le tableau :

x	- 20	-15	-10	-5	-3	+0	+2	+3	+5	+10	+20
3x² - 2x + 14
Signe du résultat du calcul du trinôme :
Noter : Signe de « a » ou signe de « -a »

B) Avec un logiciel traceur de courbe sortir le graphique y = 3x² - 2x + 14

Calcul du discriminant du trinôme : 3x² - 2x + 14 ; ” = (-2 )² - 4 fois 3 fois 14 = 4 - 168 = -164

Pas de racine possible ( la courbe ne coupe pas l’axe des « x »)

Le discriminant étant négatif, le trinôme 3x² - 2x + 14  a toujours le signe de « a ».

Voir le trinôme - x² - 2x - 3 ; ” = -12 ;

Pas de racine possible (la courbe ne coupe pas l’axe des « x »)

A ) remplir le tableau :

x	- 20	-15	-10	-5	-3	+0	+2	+3	+5	+10	+20
- x² - 2x - 3
Signe du résultat du calcul du trinôme :
Noter : Signe de « a » ou signe de « -a »

B) Avec un logiciel traceur de courbe sortir le graphique y = - x² - 2x - 3 

Le discriminant étant négatif, le trinôme - x² - 2x -3  a toujours le signe de « a ».

CONCLUSION :

On retiendra que dans un trinôme du second degré, si le discriminant est négatif ; la courbe tracée ne coupe pas l’axe des « x » ; la factorisation est impossible ;

Et a x² + b x + c est toujours du signe de « a »

Si « a » est négatif alors a x² + b x + c < 0

Si « a » est positif alors a x² + b x + c > 0

En résume :

Si le discriminant de a x² + b x + c est négatif ; le trinôme a x² + b x + c

x
Signe de a x² +b x + c
	Signe de « a »

Cas où le ∆ est égal à 0 (” = 0)

Trinôme : x² - 12x +36

A ) remplir le tableau :

x	- 20	-10	-5	-3	0	+2	+3	+6	+7	+10	+20
x² - 12x +36								0
Signe du résultat du calcul du trinôme :	+	+	+	+	+	+	+		+	+	+
Noter : Signe de « a » ou signe de « -a »	a	a	a	a	a	a	a	a	a	a	a

B) Avec un logiciel traceur de courbe sortir le graphique y = x² - 12x +36

« a » = + 1 , le trinôme x² - 12x +36 doit avoir le signe de « a »

Le discriminant ∆ = 0 ; x₁ = x₂ = 6

Trinôme :- x² - 12x - 36

A ) remplir le tableau :

x	- 20	-10	-5	-3	0	+2	+3	+6	+7	+10	+20
-x² - 12x -36								0
Signe du résultat du calcul du trinôme :	-	-	-	-	-	-	-		-	-	-
Noter : Signe de « a » ou signe de « -a »	a	a	a	a	a	a	a		a	a	a

B) Avec un logiciel traceur de courbe sortir le graphique y = -x² - 12x -36

« a » = - 1 , le trinôme -x² - 12x -36 doit avoir le signe de « a »

Le discriminant ” = 0 ; x₁ = x₂ = 6

En résumé :

Si « a » > 0

x		6
Signe de x² - 12x +36
	+	0	+

Et si a < 0

x		-6
Signe de -x² - 12x - 36
	-	0	-

On peut observer que le signe du trinôme a x² + b x + c dépend du signe de « a »

x		x1
Signe de a x² +b x + c
	Signe de « a »		0	Signe de « a »

i19 et

Résolution d’inéquations du second degré à partir d’un tableau des signes.

. I ) Résolution des inégalités du second degré :

Une inégalité du second degré à une inconnue peut être ramenée à l’une des formes :

a x² + b x + c > 0

ou

a x² + b x + c < 0

Procédure :

Calculer le discriminant ”; raisonner sur le signe de « a »,

- pour «  a x² + b x + c < 0 » ; prendre les valeurs ,qui vérifient l’inégalité , inférieures à zéro.

- pour «  a x² + b x + c > 0 » ; prendre les valeurs ,qui vérifient l’inégalité ,supérieures à zéro.

Construire le tableau des signes ( vous aidez avec des valeurs numériques intermédiaires qui ne sont pas « racines ».)

Exemple 1 :

Résoudre : x² + 2x - 15 > 0

1°) Calcul du ∆ ; x’ = -5 ; x’’ = +3

2°) Tableau :

x	-10	-5	0	+3	10
Signe de x² + 2x - 15
	+	0	-	0	+

3° conclusion : L’inégalité x² + 2x - 15 > 0 est donc vérifiée pour x < -5 et x > 3

Exemple 2 :

Résoudre : x² + 2x - 15 < 0

1°) Calcul du ∆ ; x’ = -5 ; x’’ = +3

2°) Tableau :

x	-10	-5	0	+3	10
Signe de x² + 2x - 15
	+	0	-	0	+

3°) Conclusion : L’inégalité x² + 2x - 15 < 0 est donc vérifiée pour - 5 <  x  < +3

Exemple 3 : 3x² - 2x + 14 > 0

Calcul du discriminant du trinôme : 3x² - 2x + 14 ; ∆ = (-2 )² - 4 fois 3 fois 14 = 4 - 168 = -164

Pas de racine (3x² - 2x + 14  sera toujours différent de zéro)

2°) Tableau : (on prend quelque valeur simple pour calculer)

x	-10	-5	0	+3	10
Signe de 3x² - 2x + 14
	+	+	+	+	+

3°) l’inégalité 3x² - 2x + 14 >0 est vérifiée quelque soit les valeurs de « x » .

Attention : l’inégalité 3x² - 2x + 14 < 0 n’est pas possible !!!!!

Exemple 4 : résoudre - x² - 2x - 3 < 0 ;

1°) calcul du ∆ = -12 ; pas de racine

2°) tableau

x	-10	-5	0	+3	10
Signe de -3x² - 2x - 3
	-	-	-	-	-

3°) l’inégalité - x² - 2x - 3 < 0 est vérifiée quelque soit les valeurs de « x » .

Attention : l’inégalité - x² - 2x - 3 > 0 ; n’est pas possible !!!!!

Exemple 5 : résoudre -x² - 12x -36 < 0

1°) calcul de ∆ = 0 ; x₁ = x₂ = - 6

2°) Tableau

x	(-10)	-6	(0)
Signe de -x² - 12x - 36	(-16)		(-36)
	-	0	-

3°) l’inégalité -x² - 12x -36 < 0 est vérifiée pour toutes les valeurs de « x » sauf pour « -6 »

Attention : L’inégalité -x² - 12x -36 > 0 est impossible.

Exemple 6 : résoudre x² - 12x +36 > 0

1°) calcul de ∆ = 0 ; x₁ = x₂ = - 6

2°) Tableau

x	(-10)	6	(0)
Signe de x² - 12x +36	(+16)		(36)
	+	0	+

3°) °) l’inégalité x² - 12x +36 > 0 est vérifiée pour toutes les valeurs de « x » sauf pour « 6 »

Attention :L’inégalité x² - 12x +36 < 0 est impossible

ON RETIENDRA : ETUDE du TRINOME : a x² + b x + c

1° Calcul du discriminant 

	a x² + b c + c = 0
	Calcul du discriminant : ∆ = b² - 4 ac
∆ > 0		∆ = 0	∆ < 0
Deux solutions : x’ = x’’ =		Une solution : x’ = x’’ =	Aucune solution
Factorisation possible		Factorisation possible	Factorisation impossible

2° Factorisation :

Si : ∆ > 0	Alors 2 racines : x’ =  ; x’’ = Factorisation : a x² + b x + c = a ( x -x’) ( x -x’’)
Si ∆ = 0	Alors 1 racine : x ‘ (ou) x ’’ = Factorisation : a x² + b x + c = a( x -x’)² (ou) a( x -x’’)²
Si ∆ < 0	Pas de racine : On rédige la phrase : La factorisation n’est pas possible puisque le discriminant est négatif. ( = …)

3°) Signe de a x² + b x + c :

Si : ∆ > 0

x		x1			x 2
Signe de a x² +b x + c
	Signe de « a »		0	Signe de « - a »	0	Signe de « a »

Si ∆ = 0

x		x1
Signe de a x² +b x + c
	Signe de « a »		0	Signe de « a »

Si ∆ < 0

x
Signe de a x² +b x + c
	Signe de « a »

Leçon	Titre (niveau IV)
N°	TRAVAUX d ’ AUTO - FORMATION sur le second degré

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION

EVALUATION

Série 1

Former les équations du second degré ayant pour solutions :

- 2/5 et 8

2/4 et 6

-7 et - 1/2

a+b et a -b

1/ ( a+b) et 1 / (a - b)

1 + 2 et 1 - 2

(+1) / 2 et (-1) / 2

ab et a/b

(ab) / ( a+b) et (ab) / (a - b)

Problèmes :

1°) Etant donné l’équation x² + p x + q = 0 déterminer p et q de façon que les solutions de l’équation soient égales à p et à q.

2°)Soit AH le hauteur du triangle ABC relative à la base BC . ON connaît AB = 5 cm ; AC = 4 cm . On sait que de plus BH fois DH = 135 / 16 . Calculer B C.

3°) Trouver deux nombres tels que leur différence soit 5 et leur produit 60.

4°) leur différence - 10 et leur produit - 21

Série 2

1 - Résoudre les équations suivantes :

Exercices :	Solutions	Exercices :	Solutions
1 . 4 x² + 3 x = 0		4 x² + 9 = 0
2 . 4 x² - 1 = 0		(x -1)² - 9 = 0
3. x² - x = 0		4 x² + 9 = 0
4. 2 x² + = 0		X² - 25 + 2 ( x + 5 ) = 0

2 - Indiquer si les équations suivantes n’ont pas de solution, ont une solution double ou ont deux solutions distinctes. On ne demande pas de calculer les solutions éventuelles.

x² + 5 x + 12 = 0

15 x² + 14 x + 3 = 0

25 x² - 120 x + 144 = 0

5 x² - 0,2 x + 1,6 = 0

3 - En utilisant les formules générales de résolution, résoudre les équations suivantes.

x ² - 2 x - 35 = 0

4 x² - x - 2 = 0

2 x² - 3 x + 4 = 0

x² + x - = 0

4 - Résoudre par la méthode la mieux adaptée les équations suivantes :

x² + 6 x = 0

15 x² - 17 x - 4 = 0

x² + x + = 0

5 - Dans un repère ortho normal d’unité graphique 1 cm , tracer la courbe (P) courbe représentative de la fonction définie sur R par x x²

6 - Résoudre graphiquement l’équation x² - 2x - 6 = 0

Puis résoudre algébriquement cette équation.

7 - Résoudre graphiquement l’équation x² - 2x - 1= 0

Puis résoudre algébriquement cette équation.

8 - Déterminer les nombres réels « a » et « c » de manière que l’équation « a x² + b x + c = 0 » admette pour solutions les nombres « 2 » et « -1 ».

9 - Résoudre graphiquement les équations suivantes :

A	4 x² - 8 x - 3 = 0
B	2 x² - 4 x + 5 = 0
C	4 x² - 12 x + 9 = 0

10 - Pour chacun des polynômes suivants, déterminer les racines et donner la factorisation. Etudier à l’aide d’un tableau de signes , le signe du polynôme.

x ² + 4 x - 5

x² + 3 x + 4

- 4 x² + 3 x + 1

11 - Sachant que le polynôme 2 x² + b x + c admet pour racine double le nombre « -1 » donner sa factorisation et déterminer les réels « b » et « c ».

Donner le signe du polynôme.

12 - Résoudre les inéquations suivantes :

x ( x + 5 ) > 0

x² - 4 x < 0

x² > 7

( 2x + 3 ) ( x + 1 ) "e 0

4 x² + 5 > 0

9 x² + 6 x + 1 < 0

x² + 3 x - 2 < 0

- 3 x² + 2 x + 4 > 0

13 - Déterminer l’ensemble des valeurs du réel « b » pour lesquelles le polynôme 3 x² + b x + 3 n’a pas de racines.

PROBLEMES :

1- On se propose d’étudier d’abord graphiquement, puis algébriquement la rentabilité de la fabrication d’un produit par une entreprise. Le coût total de production est donné, en milliers d’euros, par la relation :

C (q) = 2 q² + 10 q + 900 où  « q » représente la quantité produite.

La recette globale est donnée, en millier d’euros, par la relation :

R (q) = 120 q où « q » représente la quantité vendue.

On suppose que tous les produits fabriqués sont vendus.

Première partie. Etude graphique

Le plan est reporté à un repère orthogonal. En abscisse,1 cm représente « 5 » et en ordonnée,1cm représente « 500 ».

A ) on considère la fonction « f » définie sur l’intervalle [ 0 ; 60] par x 2 x² =10 x + 900

a) calculer : f ( 0 ) ; f (10 ) ; f (20 ) ; f (30 ) ; f (40 ) ; f (50 ) ; f (60 ).

b) Donner l’allure de la courbe représentative de « f ».

B ) Soit la fonction  « g » définie sur [ 0 ; 60] par x 120 x .

Tracer dans le même repère la courbe représentative de « g ».

C ) En utilisant le graphique obtenu , déterminer :

a) pour quelle valeur de « q » , la recette globale est égale au coût de fabrication ?

b) sur quel intervalle , la production est rentable ?

Deuxième partie. Etude algébrique.

a) Le bénéfice réalisé par le fabrication et la vente de « q » unités est donné par B(q) = R (q) - C (q) . Calculer B (q)

b) Résoudre l’équation x² - 55x + 450 = 0 Interpréter le résultat obtenu.

c) Résoudre l’inéquation x ² - 55 x + 450 < 0 Interpréter le résultat obtenu.