Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
DOSSIER n°1 : Problèmes du second degré : LE SECOND DEGRE
.
Résoudre un problème relevant du second degré.
|
|
|
|
Chapitres :
|
|
|
|
|
|
. |
|
|
. |
|
|
3°) Résolution de problèmes : les données sont
littérales : DISCUSSION |
. |
|
TEST |
COURS |
Interdisciplinarité : Série 1
d’exercices et problèmes résolus.
« Interdisciplinarité ». |
|
Info COURS
|
1°)Généralités |
|
On dit qu’un problème est du « second
degré » s’il conduit à la résolution d’une équation du second degré à une
inconnue.
La mise en équation d’un tel problème s’effectue
comme dans le cas des équations du premier degré.
A savoir : on désigne par la lettre « x » l’inconnue et on écrit la
relation qui permettrait de vérifier l’exactitude du résultat, si la valeur de
« x » était connue .t
On résoud ensuite l’équation du second degré
obtenue.
Comme nous l’avons déjà vu : Cette équation
pourra avoir « 0 » ; « 1 » ou « 2 » racines.
Le problème pourra donc avoir « 0 » ,
« 1 » ou « 2 »
solutions.
|
2°) Exemples de résolution de
situations problèmes
« simples » du second degré les données sont
numériques. |
|
Situation problème
1 : Trouver deux nombres connaissant leur
différence « 7 » et leur produit « 60 » .
Recherche de la solution :
Nous désignons « x » le plus petit des
deux nombres. Le plus grand sera « 7 + x »
D’après l’énoncé, si « x » est le nombre cherché , le produit « x ( x+7) = 60 »
Après développement et transformation,nous obtenons l’équation : x² + 7 x – 60 = 0
Remarque : comme les termes extrêmes sont de
signe contraire, nous en déduisons que cette équations
possède deux racines.
L’une positive te l’autre négative : ( delta = 289 )
Ces racines sont : 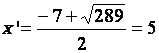 et
et 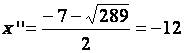
Il y a donc deux solutions : « 5 »
et « 12 » ; « -5 » et « -12 »
Situation problème
2 :
Calculer les dimensions d’un rectangle connaissant
son périmètre 20 m et son aire qui est de 21 m .
Le périmètre est égal au double de la somme
des côtés.
La somme des côtés est dons égale au demi périmètre , soit 10
m.
Désignons par « x » l’un des cotés , l’autre sera égal à « 10 – x ».
Or , l’aire
d’un rectangle est égale au produit de ses deux dimensions . Si donc « x »
est le côté cherché on doit avoir :
|
|
x
(10-x) = 21 |
|
|
Après développement : |
x
² - 10 x +21 = 0 |
|
Cette équation a deux racines qui sont :
|
|
|
|
|
|
|
|
Si l’un des
côtés du rectangle mesure « 7 m » , l’autre sera de « 3 m »
, au contraire , si l’on prend pour le
premier côté « 3 m » , le second est de « 10 – 3 = 7 m ».
On ne trouve , au fond, qu’
une seule solution.
Le rectangle cherché a pour
|
|
INTERDISCIPLINARITE :
Problème 1 : Un brocanteur achète une caisse contenant un lot
« soldé » de vases en verre blanc pour 360 € , 3 sont cassés et vend les
autres 5 euros de plus par vase qu’ils ne lui ont coûté. Il gagne ainsi 15
euros sur son marché ; combien chaque vase
lui avait-il coûté ?
Solution : soit « x » le nombre de
vases ; chaque vase lui coûte ![]() ;
il en pers 3 , donc il lui en reste « x - 3 » ; il revend
chacun 5 € de plus par vase , on il en
revend chacun «
;
il en pers 3 , donc il lui en reste « x - 3 » ; il revend
chacun 5 € de plus par vase , on il en
revend chacun « ![]() +
5 » ; cela fait ( x - 3)
(
+
5 » ; cela fait ( x - 3)
( ![]() +
5 )
+
5 )
Et ainsi il
gagne 15 euros , il
doit donc toucher 360 + 15 ou 375
€ .
On a enfin : ( x - 3)
( ![]() +
5 ) = 375
+
5 ) = 375
Soit 5x² -
30x - 1080 = 0 ou
x² - 6x - 216 = 0
Les racines sont « 18 » et
«-12 » ; le nombre « 18 » répond seul à l’énoncé
proposé ;le nombre « -12 » satisfait à
un énoncé modifié.
Problème 2 : Deux ville
« A » et « B » sont situées sur un
fleuve ;« A » à
1°) choix de l’inconnue : soit « x »
la vitesse propre du bateau.
2°) Mise en équation : Admettant que la
vitesse réelle du bateau est égale à sa vitesse propre , augmentée ou diminuée
de la vitesse du courant suivant qu’il le descend (trajet BA)
ou qu’il remonte ( trajet AB) nous exprimerons algébriquement
l’égalité :
Durée du trajet AB -
durée du trajet BA = 1 h ![]() ou
ou ![]() h .
h .
![]() -
- ![]() =
= ![]()
3°) Résolution de l’équation :
![]() -
- ![]() =
= ![]()
Supposant x¹ 4 et x ¹ -4
Multiplions tous les termes par le p.p.d.c. qui
est : 5 ( x+ 4) - 42 ( x -4) = 5 (
x² - 16)
il
vient : 210 ( x - 4) - 210 ( x- 4 ) = 6 ( x² - 16 )
soit 210 ( x + 4 - x + 4 ) = 6 x² - 96
1 680 = 6 x² - 96
6 x² = 1 680 + 96 = 1 776
x² = ![]() = 296
= 296
x = ± ![]() = ± 17,2
= ± 17,2
4°) Discussion : seule la
réponse positive convient :la vitesse propre du
bateau est de
Problème 3 :
Une amicale d’anciens élèves organise une excursion
en autocars. Le prix global de l’excursion s’élève à 1200 €. Le nombre des
participants étant supérieur de
« 4 »au nombre prévu chacun peut ainsi payer 10 € en moins. Quel
était primitivement le nombre
d’excursionnistes ?
Solution :
1°) Choix de l’inconnue : soit « x »
le nombre d’excursionnistes.
2°)Mise en équation :
Nous exprimerons algébriquement l’égalité :
« part de chaque excursionniste ans le 1er
cas » = « part de chaque excursionniste dans le second cas + 10
€ »
soit ![]() =
= ![]() + 10
+ 10
3°) Résolution de l’équation :
![]() =
= ![]() + 10
+ 10
Supposant x ¹ 0 et
x ¹ - 4 multiplions
tous les termes par le p.p.d.c.: «
x ( x+4) »
![]() =
= ![]() + 10
devient 1200 (
x + 4) = 1200x + 10 x (x+4)
+ 10
devient 1200 (
x + 4) = 1200x + 10 x (x+4)
1200
x + 4800 = 1200x + 10 x² + 40 x
10 x² + 40 x - 4800 = 0
Soit en simplifiant : x² + 4 x - 480 = 0
« a » = +1 ;
« b » = + 4 ; « b’ » = +2 ; « c » = -
480
” = 4 + 480 = 484
![]() = 22
= 22
« x’ »
= -2 + 22 = +
20
« x ’’ » = - 2
- 22 =
- 24
4°)
discussion : la solution positive convient seule. Le nombre des excursionnistes
primitivement prévu était de « 20 ».
Problème 4 : Un ascenseur
monte dans une cage d’escalier à la vitesse constante de
Quand il a parcouru
Voir dessin niveau « 0 » départ de
l’ascenseur vers le haut,la pierre est au niveau (+20) ;quand l’ascenseur
est au niveau (+10), la pierre est lachée.
Solution : En premier lieu nous remarquerons que le mouvement de la pierre étant uniformément accéléré ( @ ) , son
équation est :
e = ![]() avec « e » l’espace parcouru ;
« ³ » l’accélération ; « t » durée de parcours.
avec « e » l’espace parcouru ;
« ³ » l’accélération ; « t » durée de parcours.
Le mouvement de l’ascenseur étant uniforme, son
équation est :
e = v
t avec « e » l’espace parcouru ;
« v » la vitesse ; t la durée du parcours.
1°) Choix de l’inconnue : soit « t »
la durée de la chute de la pierre exprimée en secondes.
2°) Mise en équation :
Nous exprimerons algébriquement l’égalité :
« Chemin parcouru par l’ascenseur + chemin
parcouru par la pierre = 20 m »
10 + 2t + ![]() = 20
= 20
3°) résolution de l’équation :
10 + 2t + ![]() = 20 devient 4,9 t² + 2 t - 10 = 0
= 20 devient 4,9 t² + 2 t - 10 = 0
« a » = + 4,9 ; « b » =
+2 ; « b’ » = +1 ; « c » = - 10
” =
1 + 49 =
50
![]() #
7,07
#
7,07
t’ = ![]() # 1,25
s
# 1,25
s
t’’
= ![]() s Cette réponse négative ne peut convenir.
s Cette réponse négative ne peut convenir.
La distance du point de rencontre au haut de la
cage s’obtient en remplaçant dans la formule « e = 4,9 t² » ,
« t » par sa valeur « 1,25 ».
On trouve « e #
Problème
5 : Un détaillant en
électroménager ayant commandé des lampes de bureau pour une somme de 4375 € constate une erreur à la livraison. Le
fabriquant lui a expédié des lampes valant 3,75 € de moins par unité mais leur
nombre est supérieur de 15 au nombre de lampes commandées. Le détaillant
conserve la livraison pour le prix convenu. On demande quel était le nombre de
lampes commandées et le prix d’une lampe.
Solution :
1°) Choix des inconnues : soit
« x » le nombre de lampes commandées et « y » le prix d’une
lampe.
2°)
Mise en équations : nous exprimons algébriquement les égalités :
(1)
le prix total des lampes
dans le 1er cas est 4375 €
(2)
le prix total des lampes
dans le 2e cas est 4375 €
d’où le
système ![]()
3°) Résolution du système
Dans l’équation (2) effectuons les parenthèses et
réduisons
x y - 3,75 x + 15 y - 56,25 = 4375
x y - 3,75 + 15 y = 4 431,25 (2)
de l’équation (1) tirons
la valeur de « y » : y
= ![]()
Remplaçons « y » par son valeur dans
l’équation (2)
x × ![]() - 3,75 x + 15 ×
- 3,75 x + 15 × ![]() = 4431,25
= 4431,25
Soit
- 56,25 -
3,75 x + 15 × ![]() = 0
= 0
« x » n’étant pas nul multiplions
tous les termes par
« x »
- 56,25 x - 3,75 x² +
65 625 = 0
ou 3,75 x² + 56,25 x - 65 625 = 0
« a »
= + 3,75 ; « b » = + 56,25 ; « c » = - 65625
”
= 3164,0625 + 984375 = 987539,0625
![]() = 993,75
= 993,75
x’ = ![]() = 125
= 125
x’ = ![]() = - 140
= - 140
4°) Discussion : la réponse positive x’ = 125 convient seule.
Reportons cette valeur dans l’égalité « y = ![]() » nous obtenons
« y =
» nous obtenons
« y = ![]() =35 »
=35 »
Le nombre des lampes de poche commandées était de 125 et leur prix
unitaire de 35 €.
TRAVAUX AUTO FORMATIFS
1° ) Combien de termes composent
une équation du second degré ?
2 °) Comment nomme –t-on son premier membre ?
3°) Dans le premier membre comment nomme –t-on :
Le premier
terme ?
Le second
terme ?
Le dernier
terme ?
|
Identifier les membres et nommer les termes : |
|
|
1°)
Dans l’équation : - 3x – 1 + x2 = 0
|
|
|
2°)Dans l’équation : + x2 – 1 = 0
|
|
|
3°) ( m
+ 3 ) x2 – ( 2 – n + p )x +
m – n = 0 |
|