Pré requis:
|
la multiplication
de deux nombres entiers naturels |
|
|
la multiplication de deux nombres décimaux positifs: |
|
|
Puissance :
écriture normalisée et indicée |
ENVIRONNEMENT du
dossier
|
COURS |
Interdisciplinarité 1°)Applications en sciences 2°) série 2 |
|
|
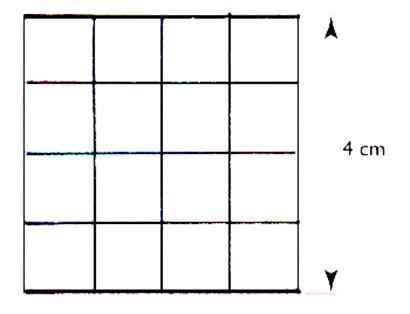
Calculer l’aire d’un carré ,
c’est chercher combien de carré de ,
par exemple Ici le carré mesure L’aire du carré est 4 Soit 16 cm² . On dit que 16 est le « carré » de 4 . On écrit :
4² = 16 ( le
« 2 » est en exposant ). On lit : « 4
au carré » ou « 4 puissance 2 » ou « 4 exposant
2 » |
|
|
Si j’écris : 3,2 2 il faudra lire suivant
« indifféremment » : « trois virgule deux au carré » ;
ou « trois virgule deux à la puissance
deux » ou ; « trois virgule exposant deux » |
Remarque : 3,2 2 est l’ écriture « algébrique » qui correspond à la
multiplication : 3,2 x 3,2 (écriture
arithmétique)
RAPPEL : Puissance d ' un
"même" nombre:
Définition :
on appelle "puissance d'un même
nombre" , la multiplication d ' un nombre par lui même deux à plusieurs fois .
X ![]() =
XXX ; X 5 = XXXXX
; X 8 = XXXXXXXX
=
XXX ; X 5 = XXXXX
; X 8 = XXXXXXXX
Ecriture:
|
Par convention
|
Avec un nombre entier positif |
Avec un nombre décimal négatif |
Un nombre quelconque représenté
par « a » |
|
X0 = 1
|
(+ 20 ) =
1 |
(-3,2) 0 = 1
|
a 0 = 1
|
|
X1
= X |
(+ 21 ) =
( + 2 ) |
(-3,2) 1 = (-3,2) |
a 1 = a |
|
X 2 = X X |
(+2 |
(-3,2) |
a |
|
Dans D+
ou D- "au carré" |
Résultat
du calcul. |
|
(+
4) (+ 4) = (+ 4)2 = |
(+16) |
|
(+ 5) ( + 5 ) =
(+ 5)2 = |
(+25) |
|
(+ 3,2) |
(+10,24) |
|
(- 3,2) |
(+10,24) |
|
(-5) ( -5 )
= (- 5)2 = |
(+25) |
Remarquer que
le carré de deux nombres négatifs est un nombre positif !!!! ( déjà vu dans la multiplication de deux nombres
relatifs négatifs)
|
Les carrés des nombres entiers naturels s ' appellent :les carrés parfaits |
|
|
Les cubes des nombres entiers
naturels s'appellent : les
cubes parfaits |
Autres exemples
:
|
4 |
5 |
|
(+4) (+4)
= (+4)2 = ( +16) |
(-5) ( -5 )
= (-5)2 = (+25) |
|
"2"
est une valeur absolue |
"3,2"
est une valeur absolue |
|
(+20 ) =
1 |
(-3,2) 0 = 1
|
|
(+ 21
) = ( + 2 ) |
(-3,2) 1 = (-3,2) |
|
(+2 |
(-3,2) |
|
(+2) |
(-3,2) |
REMARQUES IMPORTANTES:
Remarque 1
ATTENTION ! les
nombres relatifs de même valeur absolue mais de signe contraire ne sont pas des nombres égaux ; donc le produit
de l'un par l'autre ne forme un "carré" .
(-5) et (+5) ne sont pas des nombres
égaux :donc (-5)
(+5) n ' est pas la multiplication d ' un nombre par lui - même parce
que (-5) n'est pas égal à (+5)
Remarque 2
à savoir que
"par exemple":
;
|
42 = 16 |
(+4)2 = (+16) |
- 4 2 = - 16 |
(-4)2 = (+16) |
+ 42 = 16 |
|
16
Parce que 4 est un N |
(+16) Parce que (+4) est un nombre relatif |
- 16 Parce que 4 est un N précédé par le signe de la
soustraction |
(+16) Parce que (-4) est un nombre relatif |
16
Parce que 4 est un nombre N
précédé par le signe de l ' addition |
Recherche du signe du
résultat :
a) Cas où « x » est un nombre relatif positif
:
Calculs
:
|
« x n» |
« n » |
Calcul : |
Conclusion résultat |
|
(+2)2 |
Pair |
(+4) |
>0 |
|
(+2)4 |
Pair |
(+16) |
>0 |
En
conclusion : Si « x » est un nombre relatif positif
, alors le résultat de xn est
positif
b)
« x » est un nombre
relatif "négatif "
calculs :
|
« x n» |
« n » |
Calcul : |
Conclusion résultat |
|
(-2)2 |
(+4) |
>0 |
|
|
(-2)4 |
(+16) |
>0 |
|
|
(-2)6 |
|
|
En conclusion : Le
signe du résultat de « xn » dépend du signe du nombre relatif mais
aussi il dépend de la puissance « n »
si « n »
est pair dans xn ;
le résultat donné par le calcul de xn
est positif.
Cas courants (se souvenir) :
Le carré d'un nombre
relatif ( positif ou négatif ) est toujours positif.
Calculs
PARTICULIERS :
Attention : La puissance peut
agir sur un nombre relatif ou un nombre non relatif :
sur un nombre
relatif (-2)
|
Ou un nombre non relatif « 2 »
|
( -2) 4 est égal à
+16
|
- 2 4 est égal à -16
|
|
Explication : (-2)4 =
+16 la puissance agit sur (-2) Calcul
de (-2)4 = (-2) (-2) (-2)(-2) est bien égal à (+16)
|
Explication
- 24 =
-16
La puissance
agit sur le nombre non relatif :
2
Calcul : - -
24 = -16
; la puissance agit sur le
nombre non relatif.
Calcul
: - 24
= - (2
|
|
|
TRAVAUX AUTO FORMATIFS : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
CONTROLE : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1. Dans un calcul de puissance, de quoi dépend le signe du résultat ?
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculer :
Calcul mental : savoir « par cœur » les carrés parfaits
des nombres de 1 à 13 , et des dizaines et des
centaines . Remplir
le tableau suivant :
faire les Calculs (
voir les études de fonction )
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||