Pré requis:

Puissance niveau 1 écriture normalisée et indicée
Puissance niveau 2
Puissance carré :	cliquer ici

ENVIRONNEMENT du dossier

Index warmaths

Objectif précédent

Puissance carré :

Objectif suivant

Puissances des nombres relatifs .

Tableau 69

DOSSIER « calcul numérique et algébrique »:

PUISSANCE : LE "CUBE" avec les entiers ; les décimaux et les nombres relatifs (étude du signe).

- Cube d’un nombre positif.

- Cube d’un nombre relatif positif,

- Cube d’un nombre relatif négatif.

- Approche sur la puissance « n » d’un nombre relatif. ( n supérieur à 2 )

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

1°) Calcul du volume d’un cube.

Corrigé Contrôle

Corrigé évaluation

Epreuve Situation niveau 5

Fiche : n°…147……..

Activité :

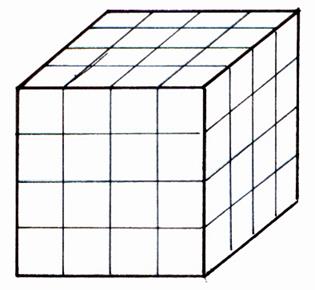
Calculer le volume d’un cube , c’est chercher combien de cubes de 1 cm³ sont contenus dans ce cube .

Le cube mesure :

L = 4 cm ; l = 4 cm , h = 4 cm .

Le volume du cube est = Ll h

Donc : 4 4 4 = 64 1 cm³ = 64 cm³

On dit que « 64 » est le cube de 4 .

On écrit : 4³ = 64

On lit : « 4 puissance 3 » ; « 4 au cube » ; « 4 exposant 3 »

cub

Rappels : « Puissance » d ' un "même" nombre:

Définition :

on appelle "puissance d'un même nombre" , la multiplication d ' un nombre par lui même deux à plusieurs fois .

X = XXX ; X ⁵ = XXXXX ; X ⁸ = XXXXXXXX

Ecriture:

Par convention	Avec un entier relatif	Avec un décimal relatif	algébre
X⁰ = 1	(+2⁰) = 1	(-3,2) ⁰ = 1	a ⁰ = 1
X¹= X	(+ 2¹ ) = ( + 2 )	(-3,2) ¹ = (-3,2)	a ¹ = a
X ² = X X	(+2 ) = ( + 2 ) ( + 2 )	(-3,2) = (-3,2) (-3,2)	a= a a
X = XXX	(+2)= (+ 2) (+ 2)(+ 2)	(-3,2) = (-3,2)(-3,2)(-3,2)	a= a a a
Ainsi de suite …….

COURS :

Le « cube » d’un nombre est le produit de trois facteurs égaux à ce nombre. On dit aussi : « Puissance trois »

CAS DES NOMBRES POSITIFS :

Exemples :

Dans N « au cube »
4 4 4 = 64	5 5 5 = 5³ = 125
(+4) (+4) (+4) = ( +64) = (+4)³	(+ 2) (+ 2)(+ 2) = (+8 ) = (+2)

On peut admettre que l’écriture « au cube » est une simplification d’écriture.

Exemples de calculs :

Dans D⁺ "au cube"	Résultat :
(+ 4 , 2 ) (+ 4 , 2 ) (+ 4 , 2 ) = (+ 4 , 2 )³ =	………………………
(+ 5) ( + 5 ) ( + 5 ) = (+ 5)³ =	(+125)
(+3,2)³ = (+ 3,2) (+ 3,2) (+ 3,2) =	(+32,768)

Les carrés des nombres entiers naturels s ' appellent :les carrés parfaits
Les cubes des nombres entiers naturels s'appellent : les cubes parfaits

CUBE d’UN NOMBRE RELATIF :

à savoir : par exemples:

(+ 3) ³ = ( +27)

( - 3 ) ³ = ( - 27 )

(+ 4) ³ = ( + 64)

(- 4)³ = (- 64)

Le cube d’un nombre relatif positif est un nombre positif.

Le cube d’un nombre relatif négatif est un nombre négatif .

On remarquera que « 3 » est un nombre « impair » .

CARRE et CUBE d’UN NOMBRE RELATIF :

Recherche du signe du résultat :

Commentaire : lorsque le nombre est positif le signe du résultat est + ;

Lorsque le nombre est négatif le résultat dépendra de la valeur « pair ou impair » de l’exposant .

a) « x » est un nombre relatif positif :

calculs :

« x ⁿ»	« n »	Calcul :	Conclusion résultat
(+2)²	Paire	(+4)	>0
(+2)³	Impair	(+8)	>0

En conclusion : Si « x » est un nombre relatif positif , alors le résultat de xⁿ est positif

CAS :« x » est un nombre relatif "négatif "

calculs :

« x ⁿ»	« n »	Calcul :	Conclusion résultat
(-2)²	pair	(+4)	>0
(-2)³	impair	(-8)	<0

En conclusion : Le signe du résultat de « xⁿ » dépend du signe du nombre relatif mais aussi il dépend de la puissance « n »

Donc avec « n = 3 » on dit que « n » est impair dans xⁿ ; le résultat donné par le calcul de xⁿest alors négatif.

Cas courants (se souvenir) :

Le cube d'un nombre relatif positif est positif;

Le cube d'un nombre relatif négatif est négatif .

REMARQUES IMPORTANTES:

(-5) (+5) (+5) n ' est pas la multiplication d ' un nombre pas le cube parce que -5 n' est pas égal à +5

à savoir :

on observera les écritures et l’on comparera les résultas dans les exemples suivants :

Cube d’un nombre entier naturel.

Cube d’un nombre entier relatif positif..

Cube d’un nombre entier naturel précédé d’un signe « moins »

Cube d’un nombre entier relatif négatif..

Cube d’un nombre entier naturel précédé d’un signe « plus »

4³ = 64

(+ 4) ³ = (+ 64)

- 4 ³ = - 64

(- 4)³ = (- 64)

+ 4³ = + 64

« 64 »

Parce que 4 est un N

(+64)

Parce que (+4) est un nombre relatif

- 64

Parce que 4 est un N précédé par le signe de la soustraction

(-64)

Parce que (-4) est un nombre relatif

+ 64

Parce que 4 est un nombre N précédé par le signe de l ' addition

Interdisciplinarité

-ALGEBRE et SIMPLIFICATION D'ECRITURE

Ou "Regroupement" de produit de facteurs :

aa = a²	Aaa = a³	abb = ab²	bbb = b³
xxx = x³	yyy = y³	xxyyy = x²y³	axxyy = ax²y²

Utilisation de la puissance « 3 » dans le résultat d’un calcul des volumes :

a) si l' unité de mesure est le mètre :

On multiplie des mètres par mètres par mètres , on écrira :" mm m " ; ce qui donne en écriture simplifiée : m ³

b) si l' unité de mesure est le décimètre :

On multipliera des décimètres mètres par des décimètres par des décimètres

On écrira : dmdm dm ; ce qui donnera en écriture simplifiée : dm ³

c) si l' unité de mesure est le centimètre :

On multipliera des centimètres par des centimètres par des centimètres

On écrira : cmcm cm ; ce qui donnera en écriture simplifiée : cm ³

d) si l' unité de mesure est le millimètre :

On multipliera des millimètres par des millimètres par des millimètres

On écrira : mmmm mm ; ce qui donnera en écriture simplifiée : mm ³

TRVAUX AUTO FORMATIFS.

CONTROLE:

1°) Que veut dire "puissance au cube » ?

2°) « x » est un nombre relatif "positif "

Quel sera le signe du résultat de « x³ » ?

3°) « x » est un nombre relatif "négatif "

Quel sera le signe du résultat de « x³ » ?

4°) Traduire en langage littéral de trois façon : (3)³

EVALUATION

1 °) Faire le calcul :

4³ =

(+ 4)³ =

- 4 ³ =

( -4)³ =

+ 4³ =

2°) Soit x = (+3,75)

Donner le signe du résultat de

	x²	x³	x⁸	x¹¹
Signe :

3°) Soit x = (- 3,734)