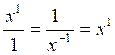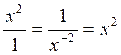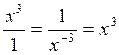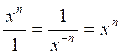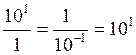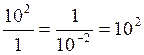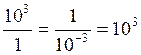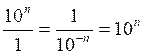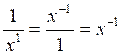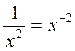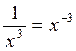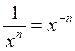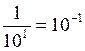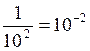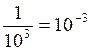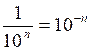|
DOSSIER : LES
PUISSANCES/ objectif cours7 |
CAP |
Pré requis:
|
Produit et multiplication: dans D |
ENVIRONNEMENT
|
Objectif précédent : 1°) puissance
d’un nombre entier 2°) |
Objectif suivant : Les puissances des nombres relatifs : (partie 3 /4 ) voir : l’exposant 0 |
|
|
|
|
|
|
|
DOSSIER : PUISSANCE Nièmes
" GENERALITES" ;(partie 2 / 5)
Écriture Normalisée et écriture indicée
|
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Définition de l’objectif :
savoir reconnaître , transformer et utiliser les « formules » sur
les puissances.
Modèle d’écriture mathématique : 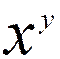
Il faut
lire : « x »
puissance « y » ou
« x » exposant « y »
Remarque :
le « y » est appelé « exposant »,il est toujours
placé dans la moitié au haut à droite du nombre .
Définition : On
appelle « puissance » n ième
du nombre « x » ,le nombre noté x n,
égal au produit de n facteurs tous
égaux à x.
On
pourra utiliser les indices pour exprimer
la puissance d' un nombre
x
n = x1 . x2
. x3 . x4. x 5 . x6
...............xn
RAPPEL :
"INDICIER" c ' est
donner un numéro d 'ordre ( indice) (à des nombres identiques ;à des lettres
identiques ;à des objets identiques dans une boite ) pour les différencier ,les
numéroter ,les ordonner . Ceux ci se trouvant
regroupés dans un ensemble donné (ou imposé)
Commentaire: dans
la vie courante des objets identiques et qui sont regroupés dans un endroit donné ,ils peuvent être différenciés avec un numéro
(indice) ou une couleur (voir les cahiers ). Lorsqu’ il y a beaucoup de produit , l’indice ne suffit plus , pour les grands magasins
qui gèrent « beaucoup » de produits on utilisera le
code barre.
Exemple : pour 10
boîtes « B » d’un même produit
on repérera la première par un nombre mis en indice « 1 », on
notera « B1 »,
Pour la deuxième boîte on notera « B2 » , et ainsi de
suite ……
Il y a Relation entre la valeur de la
puissance et la valeur indiciaire de classement :
x
n = x1 . x2
. x3 . x4. x 5 . x6
...............xn
Exemples : 5n = 51![]() 52
52![]() 53
53![]() 54
54![]() 55
55![]() 56
56![]() ............
............![]() 5n
5n
LES
PUISSANCES DE DIX :
à savoir :
|
|
Exemples appliqués aux décimaux |
Exemples appliqués aux puissances de dix |
|
x0 = 1 x0 = x0=par convention x0
=1 lire « x » puissance « 0 » (>>> info : plus sur l’exposant 0 ) |
: 5,30 = 5,30=par
convention 5,30 =1 |
100 = 100=par convention 100
=1 |
|
x = x 1 x1= x 1 ,
dans l’écriture courante x 1
= x lire « x »
puissance « 1 » |
7,21= 7,2 1
, dans l’écriture courante 7,2 1 = 7,2 |
101= 10 1
, dans l’écriture courante 10 1 = 10 |
|
x . x = ? x1 . x2 =
x2 lire « x » puissance
« 2 » ou « x » au carré » |
6,51 |
101 |
|
x x1 lire « x » puissance
« 3 » ou
« x » au cube » |
4,71 |
101 |
|
x x1 lire « x » puissance « 4 » |
2,81 |
101 |
|
x x1 lire « x »
puissance « 5 » |
|
|
|
x x1 lire :
« x » puissance « 6 » |
|
|
Commentaire
: pour trouver la puissance d’un même nombre
il suffit de compter le nombre de facteurs
communs contenu dans la
décomposition.
CAS
où l'on est présence d'un produit de facteurs
:
La valeur de l'exposant (nombre) prend la
plus grande valeur indiciaire du
facteur concerné.
Application à des produits de facteurs : on peut écrire plus simplement
|
Soit l'expression : |
|
Transformation par regroupement de facteurs |
Calculs: |
|
2 |
|
22 |
36 |
|
2 |
|
2 1 |
1350 |
|
2 |
|
23 |
33075 |
|
2 |
|
22 |
3388 |
|
2 |
|
2 2 |
500 |
|
3 |
|
33 |
1323 |
|
2 |
|
2 |
234 |
|
2 |
|
22 |
|
Exemples algébriques :
Procédure :
1°) On nous
donne une décomposition contenant deux
facteurs différents écrit sous forme de produits ( « x » ;
« y » ): " x x x y y
"
2°) on
identifie les facteurs différents ( « x » et
« y ») et on leur affecte
un indice (rang)
à chaque facteurs communs: (info @ ++)
" x x x y y " devient x1 . x2 . x3 . x4 . y1 . y 2
3°) nous
pouvons regrouper les facteurs communs et obtenir
une forme « plus concentrée » :
tel que
l'expression : " x x x y y
" s'écrira : " x 3 . y2"
Exemples
d’applications :
|
a |
= a 3 b3 |
|
5,2 |
= 5,2 3 |
|
2 |
= 2 2 = ( qui donne aussi 12 |
Remarques :
1°) L’utilisation des puissances permet de simplifier l’écriture
.
En effet les risques
d’erreurs sont moindre en notant
« x3 » ; qu’en
écrivant « x1 . x2 . x3 »
2°) Le nombre de la puissance d
'un nombre correspond au plus
haut indice du même nombre ,dans une décomposition.
PUISSANCES et écritures fractionnaires
Ces connaissances
sont nécessaires pour simplifier des écritures contenant des opérations avec des puissances ( voir l' objectif "puissances opérations")
on dit aussi : à exposant relatif
(nombre entier : positif ou négatif)
I ) Dans une écriture fractionnaire , si le
numérateur "passe" au dénominateur
la puissance du numérateur change de signe:
|
|
|
Cas général: |
Application
aux puissances de dix
|
|
|
|
Cas général: |
II )
Dans une écriture fractionnaire , si le dénominateur "passe" au numérateur la puissance
du dénominateur change de signe:
|
|
|
|
Cas général: |
Exemples d’ applications aux puissances de
dix :
|
|
|
|
Cas général: |
INFO : après avoir travaillé cet objectif (
PUISSANCE 2) ,il peut être travailler un l' objectif (PUISSANCE
10) ;(qui est une partie de l’application des propriétés sur
les opérations sur les puissances).Cet
objectif (PUISSANCE 10 ) concerne les opérations avec les puissances de
dix ;les connaissances qu’il apporte sont indispensables pour aborder
l’objectif sur les logarithmes ( LOG.déci.)
Calculs et encadrement
d'un résultat:
Pour les calculs de x2 et x3 ;
lorsque "x" est un nombre
décimal ,il est intéressant d 'avoir une estimation du résultat , pour
anticiper sur une éventuelle erreur on
fait un calcul par valeur approchée par excès ou par défaut
Cela s'appelle
faire un encadrement :
Voir
ENCADREMENT D’UN RESULTAT (SOS cours)
ALGEBRE
A SAVOIR !
INVERSE
d'un facteur : « inv. x1 » = x -1
|
Rappel : sur l' INVERSE d' un nombre: |
Démonstration:
a
)
On sait que : x1 peut
s'écrire sous la forme d'une fraction
![]()
![]()
b) On sait aussi que L’inverse
de x1 s ' écrit inv. x1
c
) à partir de la ligne a ) et
b)
on peut
donc écrire : inv. X1 =
inv.![]()
d)
on écrira que par convention : inv.![]() =
= ![]() = x -1
= x -1
e) En conclusion : « inv. x1 » = x -1
Traduction: l'inverse de "ix" puissance un est égal à "ix" puissance moins un.
Autrement dit :
x -1 = 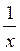 ; x -1 s’appelle l’inverse de
« x »
; x -1 s’appelle l’inverse de
« x »
SIMPLIFICATION D'ECRITURE
; la simplification est un
"Regroupement" de produit de facteurs :
|
aa = a2 |
aaaaa = a4 |
abb = ab2 |
bbb = b3 |
|
xxx
= x3 |
yyyy = y4 |
xxyyy = x2y3 |
axxyy = ax2y2 |
PUISSANCES d'un produit de facteurs (facteur contenant "plusieurs
termes" )
Rappel : sur le mot
@ facteur :
Exemple de produit de
facteurs :
(3x+1) (2x+5)
lire « facteur (3x+1)
facteur (2x+5) » ; on dit aussi « (3x+1) facteur de (2x+5) »
en conclusion : un
« facteur » peut
être aussi une suite de termes contenus
dans des parenthèses.
Activité : mettre sous forme
de puissances : (x+1) (x+1)
Commentaire:
(x+1) (x+1) lire
« facteur (x+1) facteur (x+1) » on dit aussi
« (x+1) facteur de (x+1) » ;
On remarque que les deux
facteurs contiennent les mêmes termes ,on conclut que
nous avons des facteurs communs qui
sont (x+1)
Si nous avons des facteurs communs nous
pouvons factoriser .
Voir Objectif @:
Factoriser (procédure)
(x+1) (x+1) = (x+1)2
on se souviendra que les puissances sont la première forme de
"factorisation"
Donc (a+b) (a+b)
= (a+b)2 ;
(a-b)(a-b) = (a-b)2
par contre (a+b)(a-b) reste égal à (a+b)(a-b) ce que
l’on peut faire :développer !
|
"Factoriser" |
|
|
"Développer" |
TRAVAUX AUTO FORMATIFS :
1°) Traduire, que faut-il lire 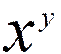 :
:
2°) Quelle Relation existe -
t -il entre la valeur de la puissance et
la valeur indiciaire de classement :
3°)Donner
la forme développer et traduire
en langage littéral.
|
|
Forme développée |
traduction |
|
x0
|
|
|
|
x 1 |
|
|
|
x2
|
|
|
|
x3
|
|
|
|
x4 |
|
|
|
x5 |
|
|
|
x6 |
|
|
4°) Pourquoi utilise-t-on
l’écriture des puissances ?
5°) A quoi est égale le
nombre de la puissance ?
6°)Compléter
les phrases suivantes
a ) - Si
« x » est positif alors xn est
b) - Si
« x » est négatif quel sera le
signe de " xn "
Cas
2 :
calculer et comparer le résultat:; mais
|
(-2)4 = |
|
|
-24 = |
|
7°) Un
carré est toujours .........
8°)
00 est une forme
9°)
0 n = ............
10° ) x -1 = ![]() ; x
-1. S’appelle.............
; x
-1. S’appelle.............
11 ) Compléter
les égalités :
|
|
|
|
|
|
|
|
|
I
)Calculer:
|
5,30
= |
|
|
100 = |
|
|
7,2 1 = |
|
|
10 1 = |
|
|
90 = |
|
|
9 1 = |
|
|
92
= |
|
|
93
= |
|
II
) Mettre sous forme de puissances:
|
6,5 |
|
|
10 |
|
|
x |
|
|
4,7 |
|
|
10 |
|
|
x |
|
|
2,8 |
|
|
10 |
|
|
2 |
|
|
x |
|
|
x |
|
|
3 |
|
|
3 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
x |
|
|
y |
|
|
y |
|
|
x |
|
|
a |
|
|
5,2 |
|
|
2 |
|
III ) Compléter le tableau suivant:
|
x |
0,7 |
9,32 |
21 |
4900 |
|
x2 |
|
|
|
|
|
x3 |
|
|
|
|