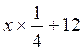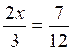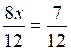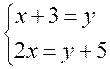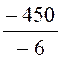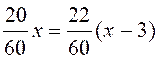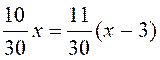|
Les égalités
(vocabulaire et théorèmes) |
|
|
|
|
|
Résolutions de système d’équations du premier degré à deux
inconnues |
|
|
Résolution
d’équations du premier degré à plusieurs termes. |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : 1°) Problèmes d’arithmétique
relevant du premier degré. 2°) Résolution d’une
équation du premier degré à 1 inconnue. |
Objectif
suivant : |
||
|
|
|
|
|
DOSSIER : GENERALITES sur la résolution des problèmes du premier degré
|
TEST |
COURS |
interdisciplinarité : |
|
Rappel : l’équation est une
égalité qui renferme au moins une inconnue et qui ne peut être vérifiée que
lorsque certaines valeurs numériques, qu’il s’agit de trouver, sont mises à la place
des inconnues.
Les équations se
désignent par le nombre de leurs inconnues
et par leur degré.
Si l’équation n’a
qu’une inconnue, son degré est l’exposant le plus fort dont cette inconnue est
affectée dans l’équation ;
Exemples :
|
2 x + 4 = x -3 |
Est une équation
du premier degré ( à une inconnue) |
|
2 x² + 4 = x - 3 |
Est une équation
du deuxième degré ( à une inconnue) |
Fin du rappel.
Pour établir
l’équation d’un problème, il suffit de transformer l’énoncé en une égalité.
Pour cela, on remplace par une lettre, « x » habituellement, le
nombre cherché ; et l’on établit les relations qui unissent toutes les
quantités, en ne se servant que des signes employés en algèbre.
La résolution
d'un problème par l'algèbre ( on dit
aussi : recherche d’une solution algébrique ) peut se décomposer en quatre
parties:
1°) Choix de
la ou des inconnues :
On
doit choisir les inconnues de façon que leur détermination entraîne la solution
du problème. Il ne pas craindre d’introduire plusieurs inconnues ou même une inconnue
auxiliaire si cela facilite la mise en équation et la résolution.
2°) Mise en
équation :
Elle
consiste à traduire l’énoncé par une ou plusieurs égalités entre les données et
les inconnues. Dans tous les cas il faut autant d’équations que d’inconnues. Il
faut rechercher également les conditions pour que toute solution de l’équation
ou du système obtenu soit solution du problème.
3°)
Résolution des équations @ :
la résolution de l’équation ou du système obtenu c’est
la partie purement algébrique du problème.
4°)
Discussion du problème :
c’est
vérifier si la racine (s) ou solution
(s) trouvée (s) satisfait aux conditions imposées ci-dessus .
commentaire: nous avons vu la
résolution de l'équation du premier degré , nous allons traiter successivement
de
|
1°) choix de la ou des inconnues: |
2°) mise en équation: |
3°) résolution d’une équation, ou d’un système
d’équations du premier degré à 1 ou 2 inconnues |
4°) discussion du problème: |
Pour vous
aider à comprendre la démarche à employer pour résoudre un problème du premier
degré à une inconnue, dans le cours qui suit nous aiderons continuellement des 4 problèmes
types :
Problème 1
|
Enoncé du problème |
|
|
On veut partager une somme de 60 000 € entre
trois héritiers, de manière que le deuxième ait 5 000 € de plus que le
premier, et le troisième 1 000 € de moins que le deuxième. Calculer la
part de chacun. |
|
Problème 2
|
Enoncé du problème |
|
|
Une marchande apporte au marché un panier de
pommes ; elle vend d’abord le Combien avait-elle de pommes ? |
|
Problème 3
|
Enoncé du problème |
|
|
Un jardin rectangulaire de |
|
Problème 4
|
Enoncé du problème |
|
|
Un père a 38 ans, son fils a 14 ans . On demande
dans combien d’années le père aura juste 3 fois l’âge de son fils. |
|
1°) choix de la ou des inconnues
Exemples de
problèmes types (recherche de l’inconnue ):
Problème 1
|
Enoncé du
problème |
Choix de
l’inconnue : |
|
On veut
partager une somme de 60 000 € entre trois héritiers, de manière que le
deuxième ait 5 000 € de plus que le premier, et le troisième 1 000
€ de moins que le deuxième. Calculer la part de chacun. |
Appelons
« x » la part du premier. |
|
Enoncé du problème |
Choix de l’inconnue : |
|
Une marchande apporte au marché un panier de pommes ; elle vend
d’abord le Combien avait-elle de pommes ? |
Soit « x » le nombre de pommes apportées. |
|
Enoncé du problème |
Choix de l’inconnue : |
|
Un jardin rectangulaire de |
Soit « x » la largeur
du 1er terrain, la largeur du 2e terrain
sera : x + 1,5 |
|
Enoncé du problème |
Choix de l’inconnue : |
|
Un père a 38 ans, son fils a 14 ans . On demande dans combien d’années
le père aura juste 3 fois l’âge de son fils. |
Soit « x » le nombre cherché, ou le nombre d’années à venir. |
Commentaires : Lorsque l'on veut résoudre un problème par
l'algèbre, la première question que l'on doit
se poser est relative au choix des inconnues.
On
peut procéder de la façon suivante:
A
) quelles quantités prend-on comme inconnues ?
|
Le problème posé, dans ses questions élémentaires, l'énoncé indique généralement
d'une manière assez claire par elle même quelles
inconnues il faut choisir. C'est surtout l'étude de nombreux exemples qui
peut servir de guide pour choisir, dans certains cas, certaines inconnues de
préférences à d'autres :il en résulte parfois des simplifications assez
grandes. |
B
)Comment sont-elles définies en valeur absolue ?
|
Les quantités que l'on prend pour inconnues étant déterminées, il est
essentiel de définir d'une manière précise de quelle manière on les
représente par des nombres ,
puisque ce sont des nombres seulement qui figurent directement ou non dans
les formules d'algèbre. Pour cela , il faut fixer d'une manière précise l'unité que l'on choisit afin de connaître la signification de ce
nombre . Pour une longueur il faut savoir si le résultat est exprimé en mètres
, décimètres , centimètres ou millimètres Pour une surface , il faut savoir si l' unité est le mètre carré ou le
décimètre carré ,… Pour le temps il faut savoir si le nombre est exprimé en année , jours
, heures , minutes , secondes …. De plus dans certains cas , il est nécessaire de fixer une origine si l'inconnue est un
temps (par exemple), un prix de départ, une caution …. |
C
)Comment sont-elles définies en signe ?
|
Dans de nombreux problèmes , les quantités inconnues sont de nature
telle qu'on peut les considérer comme négatives ou positives ; il est donc
nécessaire , en même temps qu'on choisit une unité , de faire une convention
précise relative au signe de chacune de ces quantités. On devra se rappeler
cette convention , lorsque l'on aura obtenu la solution de manière à en
connaître la signification concrète précise. |
Problème
5
|
Exemple: |
|
Jean à 3 ans 6 mois , et pierre 18 mois ; peut-il arriver que l'âge de
Jean soit double de celui de Pierre ? Il est "naturel" de prendre pour inconnue le temps qui
sépare le moment actuel de l'époque où l'âge de Jean sera (ou a été) double de celui de Pierre. On prend donc comme origine des
temps l'époque actuelle. De plus , on devra choisir une
unité de temps , on prendra , soit le
mois , soit l'année (ici le mois semble le mieux indiqué).Enfin , on devra
indiquer si on compte les temps positif vers le futur et négatifs vers le
passé , ou inversement. Les conventions ainsi faites permettront de mettre le problème en
équation et , cette équation résolue , de discuter le résultat. |
Mettre
un problème en équation, c'est écrire les équations que les inconnues doivent
vérifier, d'après l'énoncé. Les conditions non traduisibles par des équations
sont étudiées dans la discussion. On ne s'occupe ici que des conditions qui
s'expriment par des relations entre les inconnues et les quantités données.
Les
inconnues étant représentées par des lettres "x ; y ; z " etc.…, on n'a souvent qu'à écrire les
égalités exprimées par l'énoncé en écrivant ces lettres à la place des
quantités qu'elles représentent.
On
procède comme si l'on voulait faire la vérification des relations qu'indique l'énoncé ; ces relations dans
lesquelles figurent les lettres à la place des nombres inconnus donnent les
équations du problème.
Il
peut se faire cependant que les relations indiquées par l'énoncé ne suffisent
pas à déterminer la question et notamment qu'elles ne conduisent pas à un
nombre d'équations aussi de grand que le nombre des inconnues .Il faut
connaître des propriétés nouvelles
conduisant à d'autres relations.
En
Géométrie:
S'il
s'agit d'un problème de géométrie il y aura lieu de se demander si l'on connaît
des théorèmes s'appliquant
Et
…..
S'il
s'agit d'un problème de mécanique , d'arithmétique , de physique , de chimie , etc …il y aura souvent nécessité de connaître une propriété
mécanique , arithmétique , physique ou chimique ,….que ne donne pas l'énoncé et
sans laquelle cependant le problème ne pourra être résolu.
Il
convient en tout cas d'avoir grand soin , avant d'écrire toutes les relations,
d'exprimer toutes les quantités de même nature avec la même unité et s'il y a
lieu , avec la même origine et les mêmes conventions de signes .Sans cette
précaution , les équations écrites ne signifieraient rien et on ferait des
erreurs très graves.
Prenons
un exemple: soit le problème suivant :
Deux voyageurs se déplacent sur la
route de Paris à Soissons, le premier est à
Etude
du problème: ( INFO PLUS +++++)
Nous
prendrons comme inconnue le temps "x" qui s'écoule depuis l'époque
actuelle jusqu'au moment de la rencontre , ce temps sera supposé compté
positivement vers l'avenir et exprimé en heures .
Nous
avons ainsi choisi une origine des temps
, un sens positif pour les temps et une unité de temps .
Mais
l'énoncé renferme aussi des longueurs ; nous choisirons une
origine des longueurs , par exemple Paris , un sens positif
, par exemple le sens de Paris vers
Soissons , et une unité de longueur , par exemple le kilomètre.
Avec
ces unités , la position du premier voyageur est définie par + 25 et sa vitesse
est de + 30 .Quant au second voyageur ,
sa position est définie par 500-50 = 450 , puisque Soissons est à
Ces
premiers calculs faits la mise en équation est immédiate , il suffit d' écrire
qu'au bout du temps "x" les deux voyageurs sont au même point , c'est
à dire que leurs distance du point à
Paris sont égales .or , d'après l'équation du mouvement uniforme , la
distance du premier voyageur à
Paris au bout du temps
"x" est de 25 + 30x et la distance du second est
450 - 10,8 x; l'équation du
problème est donc :
25
+ 30 x = 450 - 10,8 x
Suite
sur les problèmes types :
Après avoir identifié
l’inconnue « x » on passe à la mise en équation:
Problème
1
|
Enoncé du problème |
Mise en équation : |
|
On veut partager une somme de
60 000 € entre trois héritiers, de manière que le deuxième ait
5 000 € de plus que le premier, et le troisième 1 000 € de moins
que le deuxième. Calculer la part de chacun. |
Appelons « x » la part
du premier. On a : Part du premier : x ; Part du deuxième : x + 5 000 Part du troisième : (x + 5000) - 1000
ou x + 4 000 Il est évident qu’on obtient
l’équation : x +
x + 5 000 + x + 4000 = 60
000 |
Problème 2
|
Enoncé du problème |
Mise en équation : |
|
Une marchande apporte au marché un panier de pommes ; elle vend
d’abord le Combien avait-elle de pommes ? |
Soit « x » le nombre de pommes apportées. La marchande a vendu dans ses deux premières ventes : Il reste, avant al troisième vente : x - la 3e vente comprend :
Dans les 3 ventes, la personne a vendu : Si l’on ajoute à ce total les 18 pommes qui restent, on devra égaliser
avec le contenu total du panier. On tire donc l’équation suivante :
|
Problème 3
|
Enoncé du
problème |
Mise en
équation : |
|
Un jardin rectangulaire
de |
Soit
« x » la largeur du 1er terrain, la largeur du 2e
terrain sera : x + 1,5 Surface du
premier terrain : 50 × x = 50 x Surface du 2e
terrain : 42 × (x + 1,5 = 42 x +
63 On écrira
l’égalité suivante :
50 x - (42 x + 63 ) = 257 |
Problème 4
|
Enoncé du problème |
Mise en équation : |
|
Un père a 38 ans, son fils a 14 ans . On demande
dans combien d’années le père aura juste 3 fois l’âge de son fils. |
Soit « x » le nombre cherché, ou le
nombre d’années à venir. On écrira :
38 + x = 3 ( 14 + x) On remarquera qu’évidemment les âges du père et
du fils augmentent d’une même quantité d’années. |
La mise en équation du problème est effectué, il
reste à résoudre l'équation ou les équations ,voir (SOS cours sur les égalités)
Avant de passer à la troisième étape
« résolution de l’équation » ;il est
nécessaire de faire un rappel sur les propriétés des égalités (@) :
Définition :
une équation est une égalité qui peut subir toutes
les transformations suivantes :
|
Exemple 1 |
Règle 1 |
|
Soit l’égalité
8 = 8 Ajoutons 5 unités à chaque membre : 8 + 5 = 8 + 5 On a , encore l’égalité : 13 =
13 |
On peut ajouter un même nombre aux deux membres
d’une égalité sans altérer cette égalité. |
|
Exemple 2 |
Règle 2 |
|
Soit l’égalité
8 = 8 Retranchons 3 unités à chaque membre : 8 -
3 = 8 - 3 On a , encore l’égalité : 5 = 5 |
On peut retrancher un même nombre aux deux
membres d’une égalité sans altérer cette égalité. |
|
Exemple 3 |
Règle 3 |
|
Soit l’égalité
8 = 8 Multiplions par
3 unités chaque membre :
8 × 3 = 8 × 3 On a , encore l’égalité : 24 = 24 |
On peut multiplier les deux membres d’une égalité
par un même nombre sans altérer cette égalité. |
|
Exemple 4 |
Règle 4 |
|
Soit l’égalité
8 = 8 Divisons
par 2 unités chaque
membre : On a , encore l’égalité : 4
= 4 |
On peut diviser les deux membres d’une égalité
par un même nombre sans altérer cette égalité. |
|
Exemple 5 |
Règle 5 |
|
Soit l’égalité
8 = 5 + 3 On peut retrancher 3 unités à chaque membre : 8 - 3 = 5 D’autre part , soit l’égalité : 2 = 5 - 3 On peut ajouter 3 unités de chaque côté de
l’égalité, et l’on a : 2 + 3 = 5
|
Si l’on transporte un terme algébrique précédé du
signe + ou - , d’un membre d’une égalité dans l’autre membre, ce terme garde
sa valeur absolue, mais change de signe. |
Toutes les propriétés des égalités s’appliquent aux
équations.
|
Exemple 6 |
Règle 6 |
|
Soit l’équation 5 x = 20 Divisons les deux membres par « 5 », on
obtient : x
=
x = 4 |
Dans une équation, pour chasser le coefficient de
« x », il suffit de diviser les deux membres par ce coefficient. |
|
Exemple 7 |
Règle 7 |
|
Soit l’équation
On a deux fractions qu’on peut réduire au plus
petit commun dénominateur. Celui - ci est 12 Effectuons, on a :
multiplions les deux membres par 12, on
a : 8 x = 7 et x
= |
Lorsqu’ une équation présente des dénominateurs
différents, on réduit tous les termes au même dénominateur. On supprime
ensuite ce dénominateur commun. Remarque : la
suppression des dénominateurs s’appelle « chasser les
dénominateurs ». |
3° ) Résolution des
équations :
Toutes les propriétés des égalités s’appliquent aux
équations.
Résoudre une équation, c’est
« transporter » les termes inconnus d’un côté du signe
« = » et les termes connus de l’autre côté, de manière à trouver la valeur
de l’inconnue.
Pour cela, on appliquera les 7 règles qui précédent. et qu’il faut connaître
« par cœur ».
Reprenons la résolution des équations posées par
les problèmes 2 ;3 ;4 ;5 .
Problème 1 :
on a à résoudre l’équation trouvée :
x+ x + 5 000 + x + 4 000 = x
On gardera tous les « x » du même côté de
l’égalité, ce qui fera « 3x », et l’on fera passer les nombres
5 000 et 4 000 du côté opposé. D’après les règles précédentes, on
aura : x + x + x = 60 000
- 5 000 - 4000
3 x = 51 000
x = 17 000
La part du 1er héritier sera de
17 000 €
Le 2e héritier aura : 17 000 +
5 000 = 22 000 €
Le 3e héritier aura 22 000 - 1000 = 21 000 €
Commentaire :
le résultat est positif et devaient l’être forcément.
Vérification : 17 000 + 22 000 + 21 000 =
60 000 €
Remarque : ici , l’équation était
« simple » , et ne présentait aucun dénominateur à faire disparaître.
On a à résoudre
l’équation trouvée : 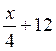 +
+ 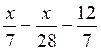 + 18 = x
+ 18 = x
Il faut chasser les dénominateurs. Le plus petit
dénominateur commun sera « 28 ». En réduisant tous les termes à ce
dénominateur, on aura :
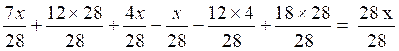
Faisons disparaître le dénominateur
« 28 ».
7 x + 336 + 4x - x - 48
+ 504 = 28 x
Faisons passer tous les termes en « x » du
côté droit de l’équation, et l’on aura :
336
- 48 + 504 =
28 x - 7 x - 4x + x
ou
792 = 18 x
ou 18 x = 792
et en chassant le coefficient
« 18 » : x = ![]() = 44
= 44
Conclusion : le nombre
primitif de pommes était : 44
Remarque 1 : ce nombre est
positif est devait l’être.
Remarque 2 : Si l’on fait
passer les termes inconnus du côté droit de l’équation, c’est qu’on s’était assuré
rapidement qu’il y avait moins d’ »x » à gauche de l’équation qu’à
droite, et qu’on aurait un nombre positif d ‘ « x » à droite .
C’est une précaution importante. Sans cela on aurait eu : - 18 x = - 792
Et il aurait fallu changer tous les signes de l’équation, ce qui pourtant n’altérait pas le
résultat de l’équation.
Problème N°3 On a à résoudre l’équation trouvée 50x - ( 42x + 63) =
257
On fait disparaître les parenthèses : 50 x - 42 x - 63 = 257
On réduit :
8 x = 257 + 63
8x = 320
x = 40
conclusion : la largeur du terrain sera de
Problème N°4
On a à résoudre l’équation trouvée 38 +
x = 3 ( 14 + x )
Faisons disparaître les
parenthèses en faisant la multiplication :
38
+ x = 42 +3x
Faisons passer les « x » à droites, on
obtient :
38 - 42 = 3 x - x
- 4 = 2 x
- 2 = x
ou x = - 2
On obtient ici une valeur négative
« -2 », qui peut facilement s’interpréter. On demandait dans combien
d’années l’âge du père serait égal à 3 fois l’âge de son fils. On trouve que ce
nombre d’années est -2 . Cela veut dire qu’il y avait « déjà » 2 ans
que la condition posait avait été réalisée. En effet, 2 ans auparavant, l’âge
du père était 36 ans et l’âge du fils 12 ans.
Il faut
discuter les résultats. voir ce qui suit :
4°
) DISCUSSION des résultats:
La résolution
de l'équation ou des équations
d'un problème est déterminée,
impossible ou indéterminée.
Si elle est impossible : il n'y a pas de solution
ou racine.
Si elle est indéterminée, il faudra lever
l'indétermination.
Remarque : on verra plus tard que ces cas
d’impossibilité et d’indétermination trouve surtout leur application dans la
résolution des équations du 1er degré à plusieurs inconnues ( @ )
et des équations du 2e degré.
Si elle est déterminée:
Elle conduit à des nombres qui peuvent être
positifs ou négatifs , entiers , fractionnaire ,…
Discuter le problème , c'est examiner quelles conséquences
on peut déduire de ces divers circonstances au point de vue de la solution du
problème.
Par exemple , supposons que la lettre "x"
représente le nombre de femme composant
une assemblée et que nous avons x =![]() , ou bien
x = -13 , nous devrons en conclure que , si nous n'avons pas fait d'erreur de calcul , le
problème proposé est impossible. De même si
pour l'un des chiffres d'un
nombre , on trouve 14 (par exemple), nombre supérieur à 9 , de même si l'on
trouve un nombre négatif pour le salaire d'une personne , un nombre supérieur au rayon pour la
distance d'une corde au centre de la circonférence.
, ou bien
x = -13 , nous devrons en conclure que , si nous n'avons pas fait d'erreur de calcul , le
problème proposé est impossible. De même si
pour l'un des chiffres d'un
nombre , on trouve 14 (par exemple), nombre supérieur à 9 , de même si l'on
trouve un nombre négatif pour le salaire d'une personne , un nombre supérieur au rayon pour la
distance d'une corde au centre de la circonférence.
Nous
allons montrer sur des exemples comment on discute un problème ; cette
discussion est généralement très aisée dans le cas où les données sont numériques ; elle est
souvent plus longue lorsque ces données , ou certaines d'entre elles , sont
représentées par des lettres dont la
valeur numérique n'est pas connue. Pour faire une discussion complète , il est
alors nécessaire d' examiner successivement les divers hypothèses que l'on peut
faire sur le signe et la grandeur relative des données. Tout cela sera rendu
plus clair par l' étude de quelques exemples.
INFO
complémentaire : « PROBLEMES
du Premier degré à une inconnue. »
On donne couramment la définition suivante :
On dit qu'un problème est un problème du premier
degré à une inconnue lorsque sa résolution se ramène à la résolution d'une équation du premier degré à une inconnue.
Cette définition est moins précise qu'elle ne le
paraît.
Lorsque l'on donne
un problème, en effet, le nombre des inconnues qu'il faut introduire
pour le résoudre dépend parfois en partie de la méthode que l'on suit.
|
Par exemple :prenons le
problème suivant Claire à 3
billes de plus que Lucile ;mais si Lucile avait deux fois plus de billes ,
elle en aurait 5 de plus que Caroline,
combien Lucile et Claire ont-il de billes chacune ? |
|
Résolution: 1er cas : On peut appeler "x" le nombre
de billes de Lucile et "y" le nombre de billes de Claire , ce qui
fait deux inconnues ; on peut aussi remarquer que , 2ème cas : si l'on appelle "x" le nombre de
billes de Lucile , l'énoncé nous apprend que le nombre de billes de Claire
est de x+3 , il est donc possible d'introduire qu'une seule inconnue. dans le premier cas , on est conduit au système : x+3 =y et 2x
= y + 5
Dans le deuxième cas , on n'a qu'une équation
à une inconnue: 2x = (x+3) +5 Il nous reste à résoudre: 2x = x +8 |
Nous pouvons trouver des analogies dans l'exemple
suivant, mais pour le degré :
|
Soit le problème : Trouver un nombre positif sachant que son
carré augmenté de 9 est égal au double de son carré diminué de 7. |
|
Résolution: Si l'on désigne ce nombre par
"x" , on a l'équation : x2 + 9 = 2 x2 -7 qui est du second degré. Mais on peut
prendre pour inconnue le carré du nombre cherché ; si l'on désigne ce carré
par "y" , on a l' équation du premier degré: y + 9 = 2y - 7 qui donne y = 16 , le nombre cherché a donc 16 pour carré , il est égal à 4. |
En
complémentaire : Autres EXEMPLES de problèmes du premier degré à une
inconnue.
|
1°) Un fermier porte au marché un certain nombre
d'œufs , qu'il compte vendre 100 centimes pièce ; il en casse 6 , mais il
trouve à vendre les autres 150
centimes pièce et rapporte ainsi chez lui 10 francs de plus qu'il ne comptait
en partant. Combien avait-il d'œufs? |
|
On désigne par "x" le nombre
d'œufs qu'il avait au départ ; la somme que le fermier comptait rapporter
chez lui sera désignée par 10x ,si nous choisissons le centime comme unité.
L'énonce nous apprend qu'il vend x-6 œufs à 15 centimes , ce qui lui rapporte
(x-6) 15 , et qu' il obtient ainsi 10 francs , c'est à dire 1000 centimes de
plus qu'il ne comptait ; l'équation du problème est donc : (x-6)150 = 100 x+1000 on en conclut :que 50x = 1900 x = 38 La réponse est donc : le fermier avait au départ 38 œufs. Il n'y a pas de discussion,
cette solution convenant parfaitement à la question posée. Il est bon de
vérifier le résultat ; s'il ne satisfait pas aux conditions du problème , on devrait en
conclure que l'on a fait quelque erreur et chercher à la découvrir. On voit que 38 œufs à 100 centimes donnent 38 Francs; si l'on à 6œufs
de moins , c'est à dire 32 , mais qu'on les vende 150 centimes on obtient 48
francs, c'est bien 10 franc de plus. Le résultat trouvé est donc exact. |
|
Pb N°2 : Un marchand de vin désire obtenir |
|
Résolution: Désignons par "x" le nombre de litres de vin à 3,50 euros,
puisqu'il faut On a donc l'équation: 3,50 x + 9,50 (100 -
x ) =500 Aussi : on obtient : 3,50x + 950-9,50x=500 3,50x -9,50x = 500-
950 -6 x = -450 x = x = 75 Il faut donc prendre Une vérification s'impose :
……!!!!!!!!!!!!!!!!!!!!! |
|
Pb N°3 : Un voleur s'est emparé
d'une bicyclette et s'enfuit sur une route avec une vitesse de |
|
Résolution: Désignons par "x" le temps cherché , exprimé en minutes ,et
compté à partir du moment où le voleur est parti ; lorsque le bicycliste le rattrape
, ils ont parcouru le même chemin , le premier ayant roulé pendant
"x" minutes avec une vitesse de
20 à l'heure et le deuxième ayant roulé pendant x-3 minutes avec une
vitesse de 22 à l'heure .Comme le chemin parcouru pendant une minute est 60
fois plus petit que le chemin parcouru pendant une heure , l' équation du
problème sera :
ou , 10x = 11(x-3) d'où x = 33 Le voleur est rattrapé 33 minutes après
sont départ . A vérifier …!!!!!!!!!!!!!!!!!!!! |
|
Pb N°4: Un père a 40 ans et son fils en a 16 ; quand
l'âge du père sera-t-il triple de celui du fils ? |
|
Désignons par "x" le temps
cherché , compté en années à partir de l'époque actuelle, et supposé positif
dans l'avenir. A l' époque "x" , l'âge du père sera 40+x et l'âge
du fils 16+x ; on doit donc avoir , d'après l'énoncé 40 +x = 3 ( 16+ x ) c'est à dire : -2x
= 8 x= -4 Discussion: Nous trouvons comme solution un nombre négatif ; or nous
avons désigné par "x" un temps compté positivement dans l'avenir ;
nous devons en conclure que c'est il y a 4 ans que l'âge du père était triple
de celui du fils. En effet , le père avait alors 36 ans et le fils 12. |
Le problème
suivant possède pas de nombres , ceux ci sont remplacés par des lettres :
|
Exemple: l'âge de Paul est représenté par
"a" et l'âge de Pierre par
"b" ; dans combien d'années l'âge de Paul sera-t-il "m"
fois plus grand que celui de Pierre? |
|
A faire ! ! ! ! ! |
CONTROLE :
1°) citer les 7 règles permettant de résoudre les
équations du premier degré à une inconnue.
2°) Donner la procédure de résolution d’un problème
(par l’algèbre):
(Citer les 4 étapes
chronologiques de la résolution d’un problème d’algèbre :
Série 1 : (traités dans le cours)
|
Enoncé du problème N°1 |
|
|
On veut partager une somme de 60 000 € entre
trois héritiers, de manière que le deuxième ait 5 000 € de plus que le
premier, et le troisième 1 000 € de moins que le deuxième. Calculer la
part de chacun. |
|
|
Enoncé du problème N°2 |
|
|
Une marchande apporte au marché un panier de
pommes ; elle vend d’abord le Combien avait-elle de pommes ? |
|
|
Enoncé du problème N°3 |
|
|
Un jardin rectangulaire de |
|
|
Enoncé du problème N°4 |
|
|
Un père a 38 ans, son fils a 14 ans . On demande
dans combien d’années le père aura juste 3 fois l’âge de son fils. |
|
Série
2.
|
1°) Un fermier porte au marché un certain nombre
d'œufs , qu'il compte vendre 100 centimes pièce ; il en casse 6 , mais il trouve
à vendre les autres 150 centimes pièce
et rapporte ainsi chez lui 10 francs de plus qu'il ne comptait en partant.
Combien avait-il d'œufs? |
|
Pb N°2 : Un marchand de vin désire obtenir |
|
Pb N°3 : Un voleur s'est emparé d'une bicyclette
et s'enfuit sur une route avec une vitesse de |
|
Pb N°4: Un père a 40 ans et son fils en a 16 ; quand
l'âge du père sera-t-il triple de celui du fils ? |