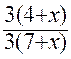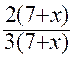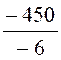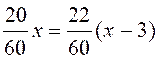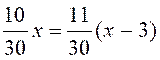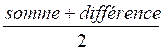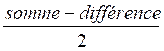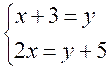|
|
COURS
|
|
|
|
Rappel : l’équation est une égalité qui renferme au moins
une inconnue et qui ne peut être vérifiée que lorsque certaines valeurs
numériques, qu’il s’agit de trouver, sont mises à la
place des inconnues.
Les équations se désignent par le nombre de leurs inconnues et par leur degré.
Si l’équation n’a qu’une inconnue, son degré est l’exposant le plus
fort dont cette inconnue est affectée dans l’équation ;
Exemples :
|
2 x + 4 = x -3
|
Est une équation du premier degré ( à une inconnue)
|
|
2 x² + 4 = x - 3
|
Est une équation du deuxième degré ( à une inconnue)
|
|
|
|
Fin du rappel.
|
|
|
|
I
) 3
Exemples de problèmes d’algèbre :
|
|
|
|
Problème N°1 : ( premier degré à 1 inconnue)
Quel nombre entier faut-il ajouter à chacun des deux
termes de la fraction :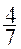 pour obtenir une fraction égale à pour obtenir une fraction égale à 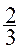 ? ?
Résolution :
Nous désignons « x » le nombre entier
positif inconnu . Nous avons :
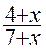 = = 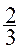
l’inconnue satisfait à cette équation.
Réciproquement , toute racine entière et positive de cette équation est une solution
du problème.
Résolution :
Le dénominateur commun est 3 (7 + x )
Nous obtenons , en
réduisant au même dénominateur :
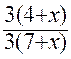 = = 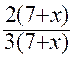
nous pouvons supprimer les dénominateurs communs .(voir les égalités)
3 (
4 +x ) = 2 ( 7 + x )
12 + 3x = 14 + 2 x
3x – 2x = 14 – 12
x = 2
cette racine ( solution)
est la solution du problème.
Vérification : à partir de 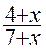 ; ;
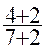 = = 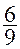 = = 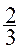
|
|
|
|
Problème N° 2 : ( premier degré à 2 inconnues)
21 livres sont
empilés les uns sur les autres ; la hauteur de la pile atteint 81 cm . Certains de ces livres ont une épaisseur de 5cm ;
les autres une épaisseur de 3cm . Trouver le nombre
de livre de chaque sorte .
Résolution :
Nous
désignons par « x » le nombre de livres de 5 cm
d’épaisseur ; par « y » le nombre de livres de 3 cm d’épaisseur.
Le nombre total de livres est de 21 . Donc x + y =
21
Les livres de 5 cm d’épaisseur ont , en centimètres , une épaisseur totale 5x ; les
livres de 3 cm
d’épaisseur ont , en centimètres , une épaisseur totale 3y. La hauteur totale
de la pile est de 81
cm .
Donc :
5x +3y =
81
Les nombres «x » et
« y » satisfont donc au système formé par les équations : x + y = 21 et
5x +3y = 81
Réciproquement, toute solution de ce système est
une solution du problème pourvu que « x » et « y » soient
tous deux entiers et positifs .
Résolvons ce système :
pourvu que
« x » et « y » soient tous deux entiers et positifs .
Résolvons ce système :
x + y = 21 ( on multiplie par -3)
et 5x +3y
= 81
ce qui donne :
-3x
+ -3y = -63
et 5x
+ 3y = 81
on additionne
les deux membres ,terme à terme ,
(5x + – 3x ) + ( 3y + – 3 y )
= 81 + (- 63)
2x + 0 = 18
soit x = 9
de l’équation
x + y = 21 ; 9 + y =
21 ; y = 12
Conclusion : il y a donc 9 livres de 5 cm et 12 livres de 3 cm , et 12 livres de 3 cm.
Vérification : 12 + 9 = 21 et
5cm fois 9 + 3 fois 12 = 81 cm
|
|
|
|
Problème N° 3 ( premier degré à 3 inconnues)
Les fortunes de trois personnes sont proportionnelles aux nombres 2 ; 3
et 5 . En additionnant le triple de la première
, le double de la seconde et la troisième , on trouve 51 000
euros . Quelles sont ces
fortunes ?
Résolution :
Désignons par « x » la fortune de la première , par « y » celle de la seconde , par « z » celle de la troisième
.
Les indications de l’énoncé se traduisent par le
système suivant :
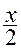 = = 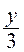 = =
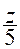 et
3x + 2y + z = 51 000 et
3x + 2y + z = 51 000
désignons par « t » la valeur commune
des rapports « 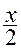 = = 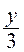 = =
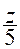 » ; » ;
x = 2t ; y =3t ; z = 5t
portons ces valeurs dans l’équation « 3x + 2y + z = 51 000 » , il vient :
6t + 6 t + 5t = 51 000
soit 17 t = 51 000 ; donc t = 51000 :
17 ; x = 3000
la première fortune
est 3000 € fois 2 = 6 000 €
la seconde fortune est 3000 € fois 3 = 9
000 €
la troisième fortune
est 3000 € fois 5 = 15 000 €
la vérification est immédiate . : 51 000 €
|
|
|
|
II
)
METHODOLOGIE :
|
|
|
|
La résolution d'un problème par l'algèbre ( on dit aussi : recherche d’une solution algébrique
) peut se décomposer en quatre parties:
1°) Choix de la ou des inconnues :
On doit choisir les inconnues de façon que leur détermination entraîne
la solution du problème. Il ne pas craindre d’introduire plusieurs inconnues
ou même une inconnue auxiliaire si cela facilite la mise en équation et la
résolution.
2°) Mise en équation :
Elle consiste à traduire l’énoncé par une ou plusieurs égalités entre
les données et les inconnues . Dans tous les
cas il faut autant d’équations que d’inconnues. Il faut rechercher également
les conditions pour que toute solution de l’équation ou du système obtenu
soit solution du problème.
3°) Résolution des équations :
la résolution de l’équation ou du système obtenu c’est la partie
purement algébrique du problème.
4°) Discussion du problème :
c’est vérifier si la racine (s)
ou solution (s) trouvée (s) satisfait aux conditions imposées ci-dessus .
commentaire:
nous avons vu la résolution de l'équation du premier degré ,
nous allons traiter successivement de
|
|
|
|
|
|
|
|
III
)
RESOLUTIONS DE PROBLEMES du Premier degré à une inconnue.
|
|
|
|
PROBLEMES du Premier degré à une inconnue.
|
|
|
|
Définition.
On dit qu'un problème est un problème du premier
degré à une inconnue lorsque sa résolution se ramène à la résolution d'une équation du premier degré à une inconnue. (Cette définition est moins précise qu'elle ne le paraît.)
Lorsque l'on donne un problème, en effet, le nombre des
inconnues qu'il faut introduire pour le résoudre dépend parfois en partie de
la méthode que l'on suit.
|
|
|
|
Autres problèmes
résolus du premier degré à une inconnue.
|
1°) Un fermier porte au marché un certain
nombre d'œufs , qu'il compte vendre 100 centimes
pièce ; il en casse 6 , mais il trouve à vendre les autres 150 centimes pièce et rapporte ainsi chez
lui 10 euros de plus qu'il ne comptait en partant. Combien avait-il d'œufs?
|
|
On désigne par "x" le
nombre d'œufs qu'il avait au départ ; la somme que le fermier comptait
rapporter chez lui sera désignée par 10x ,si nous choisissons
le centime comme unité. L'énonce nous apprend qu'il vend x - 6 œufs à 15 centimes
, ce qui lui rapporte ( x - 6 ) 15 , et qu' il obtient ainsi 10
francs , c'est à dire 1000 centimes de plus qu'il ne comptait ; l'équation
du problème est donc :
( x -6 ) 150 = 100 x+1000
on en conclut :que 50 x = 1900
x = 38
La réponse est donc : le fermier avait au départ 38 œufs. Il n'y a
pas de discussion, cette solution convenant parfaitement à la question
posée. Il est bon de vérifier le résultat ; s'il ne satisfait pas aux conditions du problème
, on devrait en conclure que l'on a fait quelque erreur et chercher
à la découvrir.
On voit que 38 œufs à 100 centimes donnent 38 euros ; si l'on à
6œufs de moins , c'est à dire 32 , mais qu'on les
vende 150 centimes on obtient 48 francs, c'est bien 10 euros de plus. Le
résultat trouvé est donc exacte.
|
|
Pb N°2 :
Un marchand de vin désire obtenir 100 litres
de vin lui revenant à 5 euros le litre en mélangeant du vin qui lui
coûte 3,50 euros
le litre avec du vin qui lui coûte 9,50 euros le litre. Combien
doit-il prendre de litres de vin de chaque espèce?
|
|
Résolution:
Désignons par "x" le nombre de litres de vin à 3,50 euros ,
puisqu'il faut 100
litres en tout
,le nombre de litres de vin à
9,50 euros est de 100-x .Le prix
total de revient des "x" litres à 3,50 et de 100-x litres à 9,50
doit être égal au prix de 100 litres à 5 euros c'est à
dire à 500 euros.
On a donc l'équation:
3,50x + 9,50(100-x)=500
Aussi : on obtient :
3,50x +
950-9,50x=500
3,50x -9,50x =
500- 950
-6 x = -450
x = 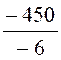
x = 75
Il faut donc prendre 75 litres à
3,50 euros et ,
par suite, 25
litres à 9,50 euros
Une vérification s'impose : ……!!!!!!!!!!!!!!!!!!!!!
|
|
Pb N°3 : Un voleur s'est emparé d'une
bicyclette et s'enfuit sur une route avec une vitesse de 20 km à l'heure ;
on s'en aperçoit 3 minutes après son départ et un bicycliste s'élance à sa
poursuite avec une vitesse de 22 km à l'heure . Au bout de combien de temps le
rattrapera-t-il ? (les vitesses sont
des vitesses moyennes)
|
|
Résolution:
Désignons par "x" le temps cherché , exprimé en minutes ,et
compté à partir du moment où le voleur est parti ; lorsque le bicycliste le
rattrape , ils ont parcouru le même chemin , le premier ayant roulé pendant
"x" minutes avec une vitesse de
20 à l'heure et le deuxième ayant roulé pendant x-3 minutes avec une
vitesse de 22 à l'heure .Comme le chemin parcouru pendant une minute est 60
fois plus petit que le chemin parcouru pendant une heure , l' équation du
problème sera :
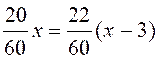
ou , 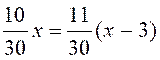 en multipliant les deux membres par 30 en multipliant les deux membres par 30
10x = 11(x-3)
d'où x = 33
Le voleur est rattrapé 33 minutes
après sont départ .
A vérifier …!!!!!!!!!!!!!!!!!!!!
|
|
Pb N°4:
Un père a 40 ans et son fils en a 16 ; quand
l'âge du père sera-t-il triple de celui du fils ?
|
|
Désignons par "x" le temps
cherché , compté en années à partir de l'époque
actuelle, et supposé positif dans l'avenir. A l' époque
"x" , l'âge du père sera 40+x et l'âge du fils 16+x ; on doit
donc avoir , d'après l'énoncé
40 +x = 3 ( 16+ x )
c'est à dire :
-2x = 8
x= -4
Discussion: Nous trouvons comme solution un nombre négatif ; or
nous avons désigné par "x" un temps compté positivement dans
l'avenir ; nous devons en conclure que c'est il y a 4 ans que l'âge du père
était triple de celui du fils. En effet , le père
avait alors 36 ans et le fils 12.
|
(SUITE de problèmes) traités en arithmétique :
|
1°)
Simon possède 220 billes ,
réparties dans 5 petits sacs. Si
l’on ajoutait 7 billes au premier sac , 3 au
deuxième et qu’on retranchât 3 billes
du quatrième et 9 du cinquième , les cinq sacs renfermeraient le
même nombre de billes. Calculer le contenu de chaque sac
.
Soit « x » le nombre de
billes contenues en moyenne dans un sac de billes ;
(x+7) + ( x
+3) + x + ( x- 6 )+ ( x-9 ) = 220
5x = 225 ; x = 225 :
5 ; x = 45
dans le premier sac il y a 45 + 7 = 52 billes
dans le deuxième sac il y a 45 +3 =
48 billes
dans le troisième il y a 45 billes
dans le quatrième sac il y a 45 – 6
= 39 billes
dans le cinquième sac il y a 45 – 9
= 36 billes
vérification : 52 + 48 + 45 +
39 + 36 = 220 billes
|
§
|
|
2° Trois
chasseurs conviennent de se partager également le gibier qu’ils tueront. A la
fin de la journée , ils n’ont tué qu’un perdreau
et un lièvre. Le premier prend le perdreau ; le second prend le lièvre et donne 30 € . au premier et 150 € . au troisième .De cette façon les parts sont égales. A quels prix ont été estimés le perdreau et
le lièvre ?
Soit « x » le
perdreau ; « x » + 30 = 150 ;le
lièvre égal 150€ ou à un perdreau plus 30 €
soit x + 30 = 150 ; d’où
x =120
le perdreau vaut donc 120 € et le
livre 150 euros
|
§
|
|
Partage
en parties inégales : dont
on connaît leur somme et leur différence.
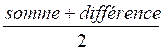 = grand nombre = grand nombre
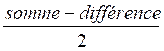 = petit nombre = petit nombre
|
|
|
3° ) On coupe un fil de fer de 45 m en 2 parties de manière que
l’une ait 9 m
de plus que l’autre. Trouver la longueur de chaque partie.
On nomme la première partie
« x » ; et la deuxième partie x+9 ; leur somme est
égale à 45 = x + x +9 ; soit 2x
= 45 – 9 ; 2x = 36 ;
x = 18 m
|
§
|
|
4°) J’ai 17 objets dans mes
deux mains .
Combien ai- je dans chaque main , s’il y en a 5 de
plus dans la main gauche ?
une main plus une main plus 5 = 17
deux mains +5 =17
deux mains = 17 – 5
deux mains = 12 ; une main
=6 ;
conclusion dans la main droite j’ai 6 objets ; dans la
main gauche j’ai 6 + 5 = 11 objets
|
§
|
|
5°) Deux paniers contiennent 180 pommes , il y an a 20 de plus
dans le premier. Quel est le contenu de chaque panier ?
Soit x le premier panier et (x +20 ) la contenance du deuxième panier la somme égale 180
je peux écrire : x + x +
20 = 180
2x + 20 = 180
2x = 180 –20
2x= 160
x = 80
|
§
|
|
Partages en 2 parts inégales :
|
|
|
6°) Caroline partage 54 euros
entre Lucile et Claire , de manière que Lucile
ait le double de Claire. Quelle est la somme d’argent que recevra
chacune ?
Claire + Lucile =Claire + 2 fois
Claire ; soit « x » = Claire
x + 2x = 54 ; donc 3x
=54 ; donc x = 54 : 3 ; x =18
conclusion Claire aura 18 € et Lucile 2 fois 18 € soit 36 €
|
§
|
|
7°) Alexandre fait deux tas avec ses 35 billes. Le second est 4 fois
plus gros que le premier. Combien chaque tas compte-t-il de billes ?
un tas plus 4 fois ce tas =
35 ; soit 5 tas = 35 ; donc un tas compte 35 :5 = 7
billes ; le plus gros tas compte 4 fois 7 billes soit 28 billes.
Vérification : 7 + 7 fois 4 = 7 + 28 soit
= 35
|
§
|
8°) Dominique et Frédérique ont reçu pour étrennes une montre et une
chaîne. Les 2 chaînes ont même valeur , mais la
montre de Dominique vaut deux fois autant que celle de Frédérique. Trouver le
prix de chaque objet , sachant que les étrennes de
Dominique valent 2400 €. et celles de
Frédérique 1500 €.
Pb plus difficile ! ! !:
Soit « y » la chaîne de Dominique et « 2x » la
montre ( =
2400 €)
Soit « x » la chaîne de
Frédérique et « x » sa montre ( = 1500€)
Nous avons un système : y + 2x =
2400 et y + x = 1500
Si l’on soustrait membre à
membre :
(y + 2x) – ( y
+x) = 2400 – 1500 : il reste :
x = 900 €
on en déduit que la montre de
Frédérique vaut 900F , et
que sa chaîne vaut 1500 – 900 = 600 €
la montre de Dominique vaut deux fois
celle de Frédérique soit 900 fois
2 ; soit 1800 €
|
|
|
|
Cas : Le problème ne possède pas de nombres , ceux ci sont
remplacés par des lettres :
|
Exemple: l'âge de Paul est représenté par
"a" et l'âge de Pierre par
"b" ; dans combien d'années l'âge de Paul sera-t-il "m"
fois plus grand que celui de Pierre?
|
|
A faire ! ! ! ! !
|
|
|
|
|
|
|
|
|
|
Par exemple
: prenons le problème suivant
Claire à
3 billes de plus que Lucile ;mais si Lucile avait
deux fois plus de billes , elle en
aurait 5 de plus que Caroline, combien Lucile et Claire ont-il
de billes chacune ?
|
|
Résolution:
1er cas : On peut appeler
"x" le nombre de billes de Lucile et "y" le nombre de
billes de Claire , ce qui fait deux inconnues ;
on peut aussi remarquer que ,*
2ème cas : si
l'on appelle "x" le nombre de billes de Lucile , l'énoncé nous
apprend que le nombre de billes de Claire est de x+3 , il est donc possible
d'introduire qu'une seule inconnue.
dans le premier cas , on est conduit au système : x+3
=y et 2x = y + 5
 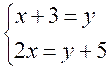
Dans le deuxième cas ,
on n'a qu'une équation à une inconnue:
2x = (x+3) +5
Il nous reste à résoudre: 2x = x +8
|
Nous pouvons trouver des analogies dans l'exemple
suivant , mais pour le degré :
|
Soit le problème :
Trouver un nombre positif sachant que son carré
augmenté de 9 est égal au double de son carré diminué de 7.
|
|
Résolution:
Si l'on désigne ce nombre par "x" , on a l'équation :
x2 + 9 = 2 x2 -7
qui est du second degré. Mais on peut prendre
pour inconnue le carré du nombre cherché ; si l'on désigne ce carré par
"y" , on a l' équation du premier degré:
y + 9 = 2y - 7
qui donne
y = 16 , le nombre cherché a donc 16 pour carré , il est égal à 4.
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO
FORMATIFS.
CONTROLE :
Citer les 4 parties de la résolution d’un
problème d’algèbre :
EVALUATION
|
1°) Un fermier porte au marché un certain
nombre d'œufs , qu'il compte vendre 100 centimes
pièce ; il en casse 6 , mais il trouve à vendre les autres 150 centimes pièce et rapporte ainsi chez
lui 10 euros de plus qu'il ne
comptait en partant. Combien avait-il d'œufs?
|
|
|
|
Pb N°2 :
Un marchand de vin désire obtenir 100 litres
de vin lui revenant à 5 euros le litre en mélangeant du vin qui lui
coûte 3,50 euros le litre avec du
vin qui lui coûte 9,50 euros le litre. Combien doit-il prendre de litres de
vin de chaque espèce?
|
|
|
|
Pb N°3 : Un voleur s'est emparé d'une
bicyclette et s'enfuit sur une route avec une vitesse de 20 km à l'heure ;
on s'en aperçoit 3 minutes après son départ et un bicycliste s'élance à sa
poursuite avec une vitesse de 22 km à l'heure .Au bout de combien de
temps le rattrapera-t-il ? (les vitesses sont des vitesses moyennes)
|
|
P b N°4:
Un père a 40 ans et son fils en a 16 ; quand
l'âge du père sera-t-il triple de celui du fils ?
|
|
|
|
|