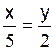Il existe une égalité avec "" dans le premier membre et un terme en "" dans le second membre ,cette égalité est appelée "équation de droite" ; elle est de la forme :

Où « » et « » sont des nombres

« » est appelé « coefficient »

« » n’a pas de nom particulier : parfois on dit « que le nombre « »que le nombre « »constante »

si « » alors l’équation aura la forme « »

si « » est égal à , alors l’équation aura la forme « »

Exemples d’équations :

Les 2 formes d'équation d'une droite :

Exemples d'équations

Equation de la forme:

« »

; ; ;

Equation de la forme :

« »

On fait varier les valeurs de « » et de « » pour obtenir une infinité d’exemples d’équations ;* « » et « » peuvent être n’importe quel nombre .

Info plus ++++ : représentation graphique d’une droite

Recherche du couple de points solution de l'équation :

Une équation du premier à deux ou plusieurs inconnues admet une « infinité » de solutions.

Activité : soit l’équation 2x + 4 y = 24 ;

( par transformation on obtient l'équation : y = -x + , ou y = - 0,5 x + 6 ) .

L'égalité est vraie si la valeur de "x" et "y" vérifie l'égalité . Une des valeurs est fausse si l'égalité n'est pas vraie .

Donc , pour trouver l'égalité vraie on fixe arbitrairement soit "x" ou soit "y"

AINSI : on donne 2x + 4 y = 24 ,trouver un couple de nombres ( x ; y ) qui vérifie l'égalité vraie .

Question : si "x" = 2 , quelle sera la valeur de "y" pour que l'égalité soit vraie ?

On fixe ( par exemple) "x = 2" et l'on remplace "2" par "x" dans 2x + 4 y = 24 ;

Alors : 2x + 4 y = 24 devient 2 2 + 4y = 21 soit 4 + 4y = 24 ,

il reste à résoudre : 4 + 4y = 24 ; 4y = 24 -4 ; 4y = 20 ; y= ; y = 5

conclusion : 2x + 4 y = 24 est vraie pour x = 2 et y = 5 .

Soit le couple de nombre est la solution ( 2;5) de l'équation : 2x + 4 y = 24

commentaire : De nombreux couples de nombres sont solutions et peuvent être mis sous forme d'un tableau .

2x + 4 y = 24	x	2	0	5	10	20	30
2x + 4 y = 24	y	5	6	7 / 2	1	-1	….

Commentaire : ce tableau est identique à celui "construit" pour obtenir les coordonnées de points , dans la fonction affine .

Complément :

On aurait pu fixer par avance une valeur numérique à " y" et en déduire par calcul la valeur de "x" :

Exemple en prenant l'égalité : 2x +4y = 21

si l’on donne à « y » la valeur arbitraire « 1 » ,

il s’ensuit que 2x +4 = 21 ,

ou 2x = 17 , ou « x » = 17/2 (ou 8,5 )

si l’on donne à « y » la valeur arbitraire « 5 » ,

il s’ensuit que 2x +20 = 21 ,

ou 2x = 1 , ou « x » = 1/2 (ou 0,5 )

De même si je donne une valeur à « x » je trouverai une valeur de « y »

Dans tous les cas on ne dira pas « résolution d'une équation du premier degré à deux inconnues » .

(par contre : on cherche à résoudre un système de deux ou plusieurs équation du premier degré à deux inconnues )

2- Transformation d’équations de la forme « ay + bx + c = 0 » pour obtenir une équation de la forme : y = f(x)

Il est nécessaire de connaître les théorèmes sur les égalités pour effectuer ces transformations :

Exemples :

	Soit l’égalité :	Par transformations successives devient l’équation de la forme : « y =…» exprimée en fonction de « x » soit « f (x) = …» On a pour habitude d’écrire que : « y = f (x) » pour dire que « y » est exprimé en fonction de « x ».
1°)	-12 y = -6x +6	y = (-6/ -12) x + ( 6 /-12) y = 0,5 x - 0,5 et alors f ( x) = 0,5 x - 0,5
2°)	4x +8 y = -40	8 y = - 4x - 40 y = (-4 /8 ) x - 40 /8 y = -0,5 x - 5 et alors f ( x) = -0,5 x - 5
3°)	2x - 3y = 13,5	3y = 2x - 13,5 y = 2x/ 3 - 4,5 et alors f ( x) = 2x/ 3 - 4,5
4°)	-3x - 9y = 18	9y = -3x +18 y = (-3/9) x + (18 /9) et alors f ( x) =(-3/9) x + (18 /9)
5°)		y = (2x) / 5 y = 0,4 x et alors f ( x) = 0,4 x

INFORMATIONS liées aux calculs précédents :

Les deux équations du premier degré à deux inconnues que nous sommes amenés à étudier sont de la forme :

Première forme:	Deuxième forme :
y = a x où « a » est un nombre et « x » la variable.	y = a x + b où « a » est un nombre et « x » la variable et « b » la constante.
Dite : équation de type "linéaire"	Dite : équation de type "affine "
Voir « COURS »	Voir « COURS »

Les deux équations sont des modèles utilisés pour traiter des situations liées aux activités humaines .

A cela s’ajoute deux autres équations :
y = k ; quelque soit la valeur de « x »
x = k ; quelque soit la valeur de « y »

A SAVOIR : On ne résout pas une équation du premier degré à deux inconnues.

On doit se ramener à une équation du premier degré à une inconnue , en fixant une valeur à une des inconnues . (il faut donner (ou attribuer) une valeur numérique à « x » ou à « y »

INTERDISCIPLINARITE:

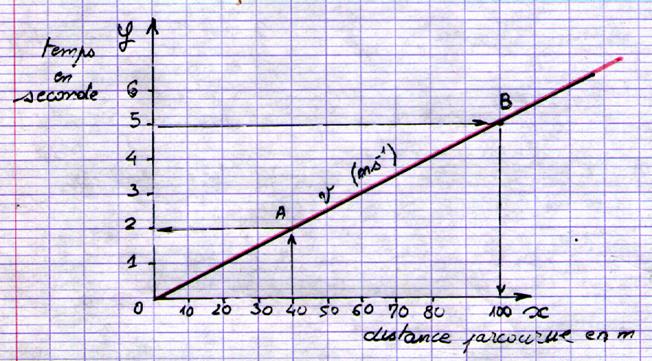
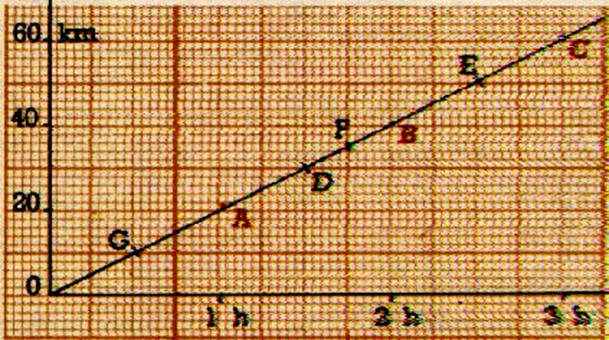
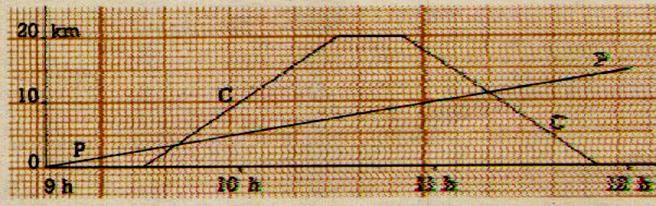
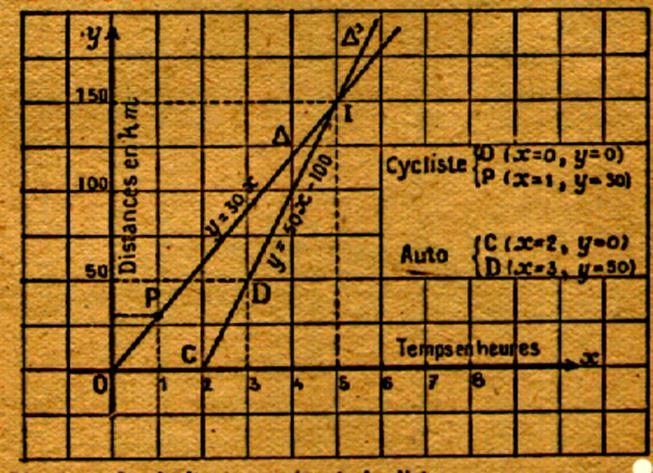
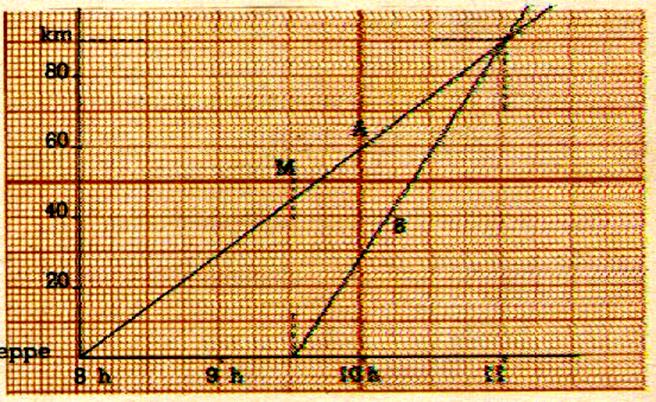
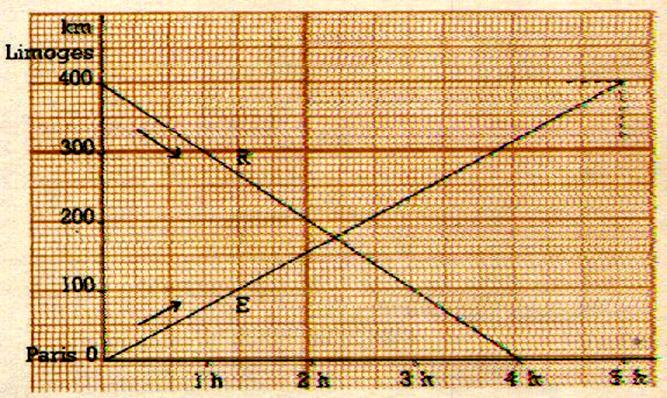
Représentation graphique de l’équation d’une droite :

Exemples d’applications :

TRAVAUX AUTO FORMATIFS

CONTROLE :

1°) Donner la forme générale de l’équation d’une droite .

2°) donner la forme générale de l’équation de droite de la fonction linéaire.

3°) donner la forme générale de l’équation de droite de la fonction affine .

EVALUATION:

Série 1
On donne l’équation y = 3,5 x ; Dans l’ exercice on donne une valeur à « x » calculer la valeur de « y »
si x = 2	alors y =
si x = -2	alors y =
si x = 3/7	alors y =
si x = 5	alors y =
si x = 3/4	alors y =

Série 2
On donne l’équation: y = a x ; on donne « x » et « y » calculer : « a »
si x = 4	et y = 6	alors a =
si x =-2,7	et y = 3,2	alors a =

Transformer l ’ égalité : si y = a x ; alors a =

(on dit :exprimer « a » en fonction de « y » et « x » ; ou autrement dit : exprimer « a » avec « y » et « x » )

Série 3 ) Calculer : trouver la valeur de « y » si l’on donne une valeur à «a » ; « x » ; « b »

(remplir le tableau suivant)

L’équation est y = ax +b

Remplacer les lettres par les valeurs données et calculer
a =	x =	b =	y = ax + b	Résultat y =
3	+2	+2
- 3	+2	+2
0.5	-2	+2
-1.5	-2	+3
1 / 3	1	-0.5
- 2 / 3	3	1,5

Chapitre 2 :

	Transformer les égalités suivantes	Les mettre sous la forme: y = (f(x)
1°)	-12 y = -6x +6
2°)	4x +8 y = -40
3°)	2x - 3y = 13,5
4°)	-3x - 9y = 18
5°)

Où « » et « » sont des nombres

Exemples d’équations :

Exemples d'équations

; ; ;

De même si je donne une valeur à « x » je trouverai une valeur de « y »

Série 1

Série 2