FONCTION LINEAIRE : RESUME
cet objectif traite des généralités sur la fonction
linéaire :
Une fonction linéaire peut s’identifier à partir de
quatre modes de représentation :
A) Equation
B) Graphe
C) Tableau
de variation (de proportionnalité)
D) Représentation
graphique.
L’
EQUATION est de la forme y = ax
exemple : y = 
x
Notation mathématique de la fonction
linéaire :
f : x
ax
exemple : f : x x
Traduction en langage littérale :
il y a « fonction » ( f)
où un nombre « x » a
pour image « » fois « x ».
(ce souvenir
que « x » est un élément de l’ensemble de départ ;que 2/3 est la relation qui permet de construire
l’ensemble d’arrivée))
Ce qu’est « x » :
« » est un nombre donné, (bien entendu différent de zéro ; dans ce cas la fonction linéaire
n’existerait pas pour 0 multiplié par « x » égal 0 ) ;
«» est appelé « coefficient directeur » dans
la représentation graphique .
« x » est la variable de la fonction.
On dira que :
La
fonction linéaire de coefficient « » fait correspondre à chaque valeur de la variable
« x » le nombre « x ».
L’équation représentant
de la fonction linéaire est une équation
du premier degré à deux inconnues de la forme
y = ax
les
deux inconnues étant « y » et « x » ;pour
« résoudre » il faudra donner une valeur à « x » pour
trouver ,par calcul, la valeur de « y » ; ou donner une valeur à
« y » pour trouver par calcul une valeur à « x ».
Exemple de calculs possibles :
soit y = x
a) soit « x = 9 » : (on peut calculer « y »)
si on donne à « x » la valeur « 9 » , alors y = .9 ; y
=18/3 ;y vaut 6
b) soit
« y = 12 » : (on peut
calculer « x »)
si on donne à y = 12 ,alors
12 = x ; x = 12 : ; donc x =18
On peut donner l’équation d’une fonction linéaire à
partir :
- d’un graphe
- d’un
tableau de proportionnalité
- d’une
représentation graphique
II ) Graphe de la fonction linéaire :
Rappels : un graphe est de la
forme :
G = {( x1 ;
f(x1)) ; (x2 ; f(x2) ) ;
......... }
puisque
« ax » = f(x) = y ; le
graphe c’est aussi : G = {( x1 ; y1) ; (x2 ;
y2 ) ; ......... }
Le graphe de la fonction linéaire est de la forme :
G = {( x1 ; ax1) ;
(x2 ;ax2 ) ; ......... }
le graphe peut être obtenu à partir :
d’une équation
d’un tableau
de variation appelé tableau de
proportionnalité.
D’une représentation graphique .(droite qui passe par l’origine)
III) TABLEAU de variation appelé tableau de
proportionnalité (regroupant les couples ( x ; ax) )
Le rapport
de « y » sur « x »
est , pour la fonction linéaire, égal au rapport « ax » sur « x » ;
Dans la fonction linéaire ce nombre est constant il
est égal à «a»
Ce nombre «a» est appelé « coefficient de
proportionnalité » ;
Le tableau s’appellera « tableau de
proportionnalité ».
Présentation du tableau de
proportionnalité :
|
relation |
|
A |
B |
C |
O |
D |
E |
|
|
|
|
ax |
x |
xA |
|
|
0 |
|
|
|
|
|
|
|
y |
yA=axA |
|
|
0 |
|
|
|
|
|
On
donne à « x » des valeurs ( choisies judicieusement) généralement
[-5 ;+5 ] (pour cette
écriture voir les « intervalles » ;Obj ;INTERVALLEdex)
Les coordonnées du point A peuvent se noter
verticalement :
A xA au lieu de A (xA ,yA)
yA
Le
coefficient directeur « a» est un
nombre relatif .
« a» peut s’appeler :
n
Coefficient de
proportionnalité (dans le tableau)
n
Coefficient directeur
de la droite de la fonction linéaire.
n
Coefficient directeur
de la droit d’équation y = ax ; dans la représentation graphique
Dans
un repère cartésien orthogonal ; dans la représentation graphique
de l’équation y = ax ; «a» est appelé « pente de la
droite », la « pente » étant
appelée aussi « tangente » ;
la
pente est obtenu par le rapport de
« y » sur
« x ».
Voir les relations
trigonométriques dans un triangle
rectangle
*On peut construire un tableau de proportionnalité
à partir :
d ’ un graphe.
D’une équation
D’une représentation graphique.
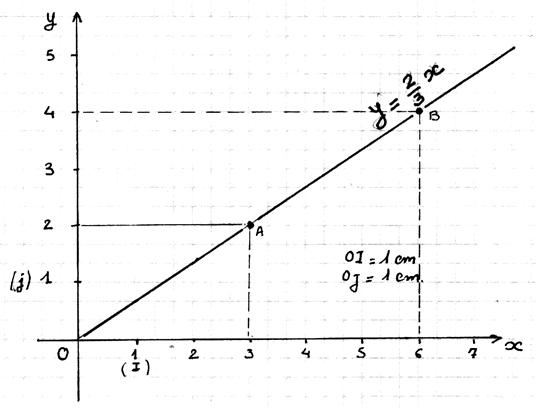
IV ) Représentation graphique de l’équation y
= ax :
la
représentation graphique de la fonction linéaire est une droite (noté xax) , où l’ensemble des points A, B ,C ,D, ........ ont pour
coordonnés les couples de nombres (x ; ax )
|
|
Caractéristiques
de cette représentation graphique :
n
c’est une droite (D)
n
cette droite passe par
l’origine « O » d ’ abscisse (0) et d’ordonnée (0) , noté (0 ;0)
n
elle possède un point
caractéristique ; à d’abscisse
valeur « 1 » correspond la
valeur de « a » ; noté P :(1 ; a)
n
« a» s’appelle
coefficient directeur de la droite ,
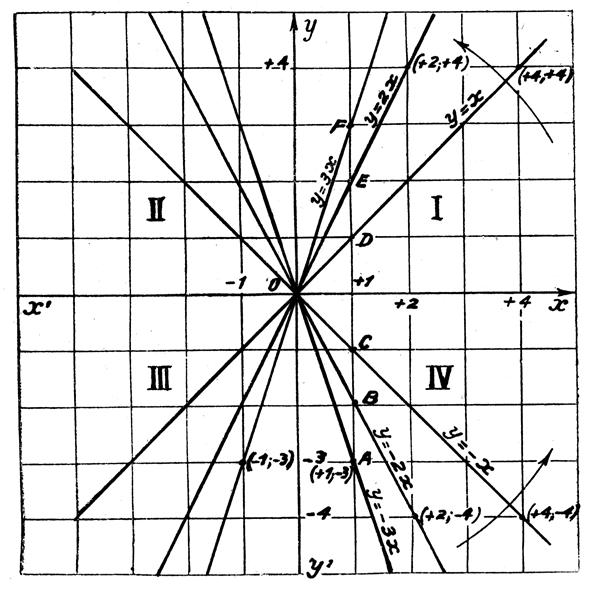
c’est un nombre relatif :, il peut être « positif » ,dans la représentation graphique la droite
monte de la gauche vers la droite ,on dira que la fonction est
« croissante », il peut - être « négatif » ,la droite
descend de la gauche vers la droite , on dira que la fonction est
« décroissante »
« a » est aussi appelé
« pente » ou « tangente » de la droite. (voir relations trigonométriques dans le
triangle rectangle )
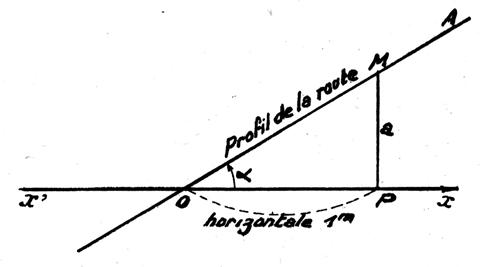
La pente
est égale au rapport de la longueur « xA » sur la
longueur « yA » ;
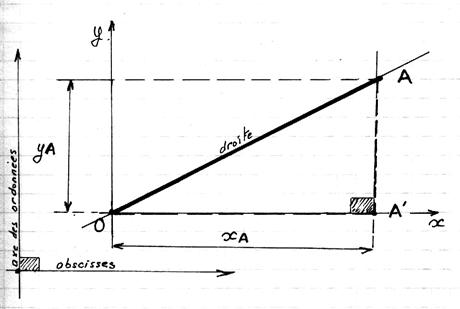
On dit
aussi égale au rapport de la longueur du segment AA’ sur la longueur du segment OA’ ;
On dit
aussi au rapport du coté opposé a l’angle (AA’ ) sur le coté adjacent
(OA’)
On dit
aussi égale à l’abscisse du point A sur
l’ordonnée du point A
Application :voir classeur (à sacnériser)
CONTROLE :
Donner la notation mathématique indiquant que l’on
a une « fonction linéaire ».
Donner la forme mathématique de « l’égalité » représentant la
fonction linéaire.
A quelle type d’équation appartient la fonction
linéaire ?
Qu’appelle-t-on variable ?
par quelle lettre la désigne-t-on ?
Soit une écriture mathématique « ax » :
à quelle opération doit -t on penser ?
comment
nomme-t-on les lettres « a »
et « x » séparé par le signe « multiplié »?
Soit la notation
« ax » dans l’équation du premier degré à deux
inconnues :
que désigne « a ». ?
Que désigne « x » ?
Donner la forme du couple qui forme
le graphe de la fonction linéaire.
Donner la forme du graphe représentant la fonction
linéaire.
Comment appelle - t- on le tableau de variation représentant la
fonction linéaire ?
Donner une représentation du tableau de variation représentant la fonction
linéaire (préciser le rôle des principaux points.
« a »
de la fonction linéaire possède
plusieurs appellations ; combien ; nommer les ?
Dans quel cas dit - on que fonction est
« croissante » ?
Dans quel cas dit - on que fonction est
« décroissante » ?
Représenter graphiquement la fonction linéaire ( une croissante
et une décroissante ) dans un repère orthonormé.
Préciser
les rôles des points particuliers.
Récapitulatif :
Nommer tous les modes de représentation de la
fonction linéaire ,préciser pour chaque cas ce qui en fait la particularité.
SOMMATIVE :
A ) On vous
donne le tableau de variation de la fonction
f1(x) :
|
x |
-2 |
-1 |
4 |
6 |
|
f1 (x) |
-3.2 |
-1.6 |
6.4 |
9.6 |
Trouvez la relation en fonction de x.
Réponse : f1(x)
=.............................
B ) On vous
donne l’expression de la fonction f2(x) .Compléter le tableau de
variation pour
f2(x)
= 3,5x
|
x |
-1,7 |
-0,25 |
0 |
|
1,35 |
|
|
f2(x) |
|
|
|
3,5 |
|
|
C) Vous
avez le tableau de variation « A » représentant f1(x) .Faire la
représentation graphique dans un repère cartésien (O,I,J) donné , où lg [OI] = 1,2cm et
[OJ] = 1,5 cm.
D ) Dans ce
même repère , la droite D2
représente la fonction g2.
Question : Compléter le tableau suivant :
|
x |
-3 |
|
1,5 |
|
6,5 |
|
|
g2 |
|
-1 |
|
3 |
|
|
E )
Représenter graphiquement les fonctions f3(x) et f4(x)
dans le repère (O,I,J)
f3(x) = -1,5 x
f4(x) =
3x
