Index warmaths

Liste des leçons

DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

ALGEBRE. N° 28

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :Formation Niveau V (inclus le CAP et CFA)

OBJECTIFS :- médiation en algèbre.

I ) Pré requis:

i9	Le calcul numérique	:i
i9	Liste des objectifs « passerelle » 3^ème / Seconde.	:i
i9	Liste des leçons	:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent  26:

Dossier suivant : 28 Problème d’application.

Info n°1 : résoudre une équation.

III ) LECON n°28 :

Problèmes du premier degré :d’application .impossible ; indéterminé, inacceptable .

IV) INFORMATIONS «  formation leçon » :

Test	COURS	Travaux auto - formation.			Corrigé des travaux auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé évaluation

V ) DEVOIRS ( écrits):

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°28	Problèmes d’application

COURS sur : INTERDISCIPLINARITE : Problèmes d’application

Info plus

La résolution d’une équation aboutit parfois à trois « propositions » de solution dont deux cas sont déroutants et un cas où la solution inacceptable.:

I) Problème impossible.

Un droguiste vend les 3/4 d’un sac d ‘ engrais moins 2 kg . Le lendemain il vend à chacun des quatre premiers clients le 1/16 d’un sac de même poids plus 1/8. A un cinquième client, il vend 5 kg, du même engrais. Il croît alors avoir vendu autant le premier jour que le deuxième. Trouver le poids d’un sac.

Résolution : Soit « x » le poids du sac en kg.

La vente du premier jour peut être représentée par :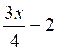

Celle du deuxième jour par :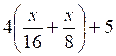

D’ après l’énoncé, on peut écrire

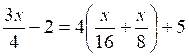
Effectuons :

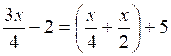
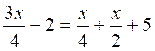
Soit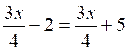

D’où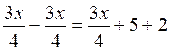

0x = 7

Il y a donc impossibilité, et le droguiste à commis une grosse erreur.

II) Problème indéterminé.

Peut -on trouver un nombre sachant que les 5/6 de ce nombre moins 1/2 valent les 7/12 de ce même nombre augmentés de son 1/4 et diminué de 0,5 ?

Soit « x » ce nombre.

On peut écrire :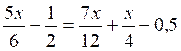

On réduit au même dénominateur.( dénominateur commun = 12)

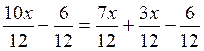
On élimine le dénominateur (cela revient à multiplier chaque terme par « 12 »

10x - 6 = 7 x +3x - 6

On réunit les « x » dans le premier membre.

10x - 7x - 3 x = +6 - 6

En réduisant 0x = 0

Conclusion : tous les nombres conviennent.

III ) Solution inacceptable.

Trouver 2 nombres entiers consécutifs dont la somme est 132.

Résolution : Soit « x » le premier nombre.

On peut écrire : x + (x +1) = 132

2x + 1 = 132

2x = 132 - 1

2x = 131

Et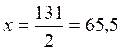

Conclusion : Comme on demande 2 nombres entiers, la solution est inacceptable. C’est que le problème a été mal donné.

I)

Leçon	Titre
N°28	TRAVAUX d’Auto - FORMATION sur Problèmes d’application

TRAVAUX N° 28 d ’ AUTO - FORMATION : CONTROLE

1. Quand dit-on qu’un problème est « impossible ».

2. Quand dit - on qu’un problème est « indéterminé »

TRAVAUX N°28 d ‘ AUTO - FORMATION EVALUATION

Problèmes :

1°) Un commerçant vend une première fois 75 kg de pomme de terre avec un bénéfice de 10% sur le prix d’achat, une deuxième fois, pour la même somme totale, 60 kg. de ces pommes de terre en faisant un bénéfice de 12,50%. Calculer le prix d’achat du kg. de pommes de terre.

2°) Calculer un nombre dont les 3/4 augmentés de son 1/8 différent de 10 unités de sa moitié augmentée de ses 3/8.

CORRIGE :

Problèmes :

1°) Un commerçant vend une première fois 75 kg de pomme de terre avec un bénéfice de 10% sur le prix d’achat, une deuxième fois, pour la même somme totale, 60 kg. de ces pommes de terre en faisant un bénéfice de 12,50%. Calculer le prix d’achat du kg. de pommes de terre.

2°) Calculer un nombre dont les 3/4 augmentés de son 1/8 différent de 10 unités de sa moitié augmentée de ses 3/8.

1°) :

1	A
2	B
3	C
4	D
5	E

Problème :

1