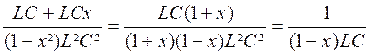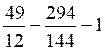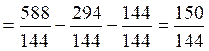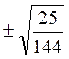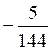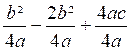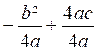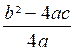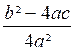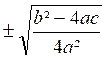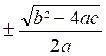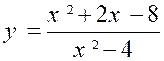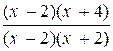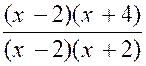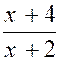Pré requis:
|
|
|
|
|
INFO :
|
1°) Résoudre. Le premier degré |
Objectifs
suivants: 2°) Résolution d’exercices
et de problèmes du second degré INFO : |
Info : Retour vers la liste des cours sur
le second degré « équations » |
DOSSIER :
Résolution des équations incomplètes et complètes
du « second degré à une inconnue ».
|
1- |
|
|
|
2 |
|
|
|
|
|
|
|
3 |
Equation complète du second degré. |
|
|
|
|
|
|
|
|
|
|
|
B)
équation à coefficients littéraux , forme générale
de résolution. |
|
|
|
|
|
|
4) |
|
|
|
5) |
|
|
|
|
Equation du second degré dans le cas où l’inconnue
est une variable restreinte. |
|
|
6) |
Equation
bicarrée. ( INFO plus ) |
|
Vocabulaire :
Attention le mot « racine » a
deux significations :
1- La
ou les « racine(s) »
pour désigner « la ou les
solutions » de l’équation .
2- La racine qui
désigne que l’on calcule la racine carrée du discriminant.
|
TEST |
COURS |
Il faut savoir refaire les exercices traités dans ce cours |
Interdisciplinarité |
|
PS : on
aborde dans ce cours la notion de
« nombre imaginaire ».
1- Définitions : Une
équation à une inconnue est du second degré, quand ses deux membres étant
entiers et ou rationnels, la plus haute puissance de « x » est la
seconde.
Exemple : Soit l’équation
x ( x -2) + 3 x = ( x -
1 ) ( 2x + 5 )
Développons les deux membres
x² -
2 x + 3 x = 2 x² + 5x - 2 x - 5
x ² + x = 2 x² + 3 x - 5
Rassemblons tous les termes dans le 1er
membre et réduisons et ordonnons :
x ² + x - 2 x² - 3 x + 5 = 0
soit : - x² - 2x + 5 = 0
Le premier membre étant un polynôme du second degré
en « x » , l’équation est un trinôme du second degré en « x » . Ainsi,
la forme générale d’une équation complète
du second degré est :
a x ² + b x + c = 0
« x » est la variable et
« a » , « b » et « c » désignant des nombres connus.
Dans l’exemple précédent a = -1 ; b = -2 ; c = + 5
Résoudre :
pour résoudre une équation du second degré
on cherche tout d’abord à réduire
l’équation ;c’est à dire passer d’une forme
« développée » à une forme « factorisée » .
En
résumé : On appelle équation du second degré dans
l’ensemble « R » toute équation de la forme :
ax2
+ b x + c = 0
Où
« a » ¹ 0 où a ; b ; c sont
des nombres réels donnés, appelés coefficients de l’équation et « x »
un nombre réel inconnu (variable).
|
Exemples d’équations du second degré « incomplète »: |
« complète » |
||
|
Cas 1 |
Cas 2 |
Cas 3 |
Cas 4 |
|
5 x2 = 0 |
x2 – 4 = 0 |
3x2 + 2x = 0 |
x2 - 6x + 8 = 0 |
2- EQUATIONS
INCOMPLETES DU SECOND
DEGRE
L’équation du second degré devient incomplète dans trois cas :
|
Cas |
Exemples |
Forme générale |
|
1er cas :
c = 0 |
x² + 2x = 0 |
a x² + b x = 0 |
|
2ème cas : b = 0 |
x² - 5 = 0 |
a x² + c = 0 |
|
3ème cas : b = c = 0 |
3 x² = 0 |
a x² = 0 |
Nota : le coefficient « a » ne peut être
nul sinon, l’équation de la forme b x + c = 0
ne serait plus du second degré.
I ) - RESOLUTION DES EQUATIONS INCOMPLETES DU
SECOND DEGRE
1°) Forme
a x² = 0
Exemple 5 x² = 0
Le premier membre est immédiatement décomposable en
un produit de facteurs du premier degré.
5 x .
x = 0
En égalant successivement à zéro chacun des deux
facteurs « 5x » et « x » on trouve chaque fois « x =
0 ». Cette réponse ayant été
trouvée deux fois , il est naturel de dire que
l’équation a deux solutions égales à zéro.
2°) Forme
a x² + b x = 0
Exemple : x² + 5 x = 0
« x » est le facteur commun au deux
termes, mettons « x » en facteur commun ( factorisons)
nous obtenons un produit de facteurs, qui doit être égal à
« 0 ». x ( x + 5 ) = 0
;
on pourrait
identifier les « x » en leur affectant un indice ,
on écrirait alors [ x1
( x2 + 5 ) ]
Les deux facteurs du premier membre sont donc « x » et « x -5)
L’équation a pour solutions les valeurs de
« x » qui annulent chacun des deux facteurs du 1er membre
soit :
x1 = 0
et x 2+ 5 = 0
ce qui donne comme les deux solutions x1 = 0 et
x2 = - 5
On résume : les
solutions pour que x² + 5 x = 0 sont
x = 0 et x = -5
3°) Forme a x² + c = 0
Exemple 1 x² - 4 = 0
On écrit x²
= + 4
; ( x1 x2
= 4 )
On en
déduit que x = ![]() ;
;
Commentaire :
« x » serait égal
à « 2 » mais ; mais on se souvient que ( +2) ² = 4 et que
(-2)² = 4 ; on devra conclure que
L’équation a pour solution x = +
2 ou x = - 2 on peut écrire x = ± 2 ou x
= ± ![]()
Attention : -2 et +2
ne peuvent pas être solutions en même temps, en effet , -2 fois + 2 = - 4
Ou x1 et x2 ont pour valeur - 2
; ou x1 et x2 ont pour valeur +2
Exemple II : x² + 3 = 0
X² =
-3 or , nous avons vu qu’il n’existe
aucun nombre dont le carré soit négatif . Nous dirons donc qu’il y a
impossibilité.
On interprète parfois ce résulta
d’une autre façon. Le nombre imaginaire
Posant x = ![]() et , admettant
toujours que
et , admettant
toujours que ![]() ne représente aucune quantité réelle, c’est à
dire calculable on qualifie d’ « imaginaire » cette racine carrée
singulière d’un nombre négatif ; on
dit alors que l’ équation admet deux solutions imaginaires : x
=
ne représente aucune quantité réelle, c’est à
dire calculable on qualifie d’ « imaginaire » cette racine carrée
singulière d’un nombre négatif ; on
dit alors que l’ équation admet deux solutions imaginaires : x
= ![]() ou x
=
ou x
= ![]()
INFORMATION : du réel à
l’imaginaire
Au XVI e siècle, l’ Italien
Cardan lève une interdiction célèbre entre toutes : il imagine qu’un
nombre négatif peut admettre une racine carrée. Ainsi était créé l’ensemble des
nombres complexes.
Deux siècles plus tard, suisse Euler utilise la
lettre « i » en lieu et place de la notation pour le moins ambiguë
« ![]() ».
».
Le nombre « i » est un nombre imaginaire,
dans le sens où il ne peut être un nombre réel !!!!
Depuis, la théorie des nombres complexes n’a cessé
de progresser et de trouver des applications dans divers domaines tels que l’électricité, l’électronique
….
Remarque : la lettre « j » est
souvent préférée à « i » afin d’éviter, lors de certaines applications en électricité toute
confusion avec l’intensité du courant.
Pour plus d’information voir le cours sur
« les nombres complexes »
PARTIE N° 2
Remarque : Pour résoudre une équation du
second degré on cherche à réduire
l’équation c’est à dire passer d’une forme « développée » à une forme
« factorisée ». Plusieurs méthodes peuvent être utilisées.
A - EQUATION COMPLETE A COEFFICIENTS
NUMERIQUES.
Exemple 6 x² + 7 x + 1 = 0
Pour réduire cette équation, nous emploierons la
« méthode des coefficients indéterminés » dont les applications sont innombrables.
Ayant remarqué, que l’équation du second degré se
résout facilement lorsqu’elle ne contient pas
de terme du premier degré, de la forme
a x² + c = 0 , nous décidons de changer
d’inconnue. Posant « x = X + K », nous fixerons la valeur du
coefficient « K » de façon à
obtenir une équation du second degré en
« X », ne contenant pas de terme du premier degré. La valeur de
« K » étant déterminée et celle de « X » étant calculée
nous en déduirons « x ».
( « X » lire « grand ixe ;
« x » lire petit ixe)
|
soit
: x = X + K |
(1) 6 x² + 7 x + 1 = 0 |
|
remplaçons « x » par sa valeur |
6 ( X + K ) ² + 7 ( X + K) +
1 = 0 |
|
Développons le premier membre |
6 ( X ² + 2 X K + K ² )+ 7 X + 7K + 1 = 0 6 X ² + 12 X K + 6K ² + 7 X
+ 7K + 1 = 0 |
|
Mettons X
en facteur commun |
(2) 6 X² + X (12 K + 7) + 6 K² + 7 K + 1 = 0 |
|
Le terme du premier degré X (12K +
7) disparaîtra si le coefficient 12K + 7 est nul |
Soit : 12 K + 7 = 0 12 K = -7 K = |
|
Remplaçons « K » dans l’équation (2) |
6 X² + X ( 12 × 6 X² +
0 + 6 X² = |
|
Calcul des valeurs de « X » |
X² = |
Remplaçons X et
K par leurs valeurs dons
l’expression « x = X +
K » il vient :
x
’ =  =
= 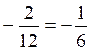
x ‘’ =
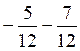 =
= 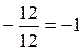
B - EQUATION
COMPLETE A COEFFICIENTS LITTERAUX. ( première forme) FORMULE GENERALE
DE RESOLUTION.
Si nous résolvons par la même méthode l’équation à
coefficients littéraux a x² + b x + c =
0 , nous obtiendrons une formule applicable ensuite à
n’importe quelle équation numérique, à la condition d’ y remplacer
« a » , « b », « c » par leurs valeurs.
Posons x =
X + K ;et reportons cette valeur dans
l’équation a x² + b x + c = 0 (1)
|
Soit
« x » = « X + K » |
Remplaçons : a (X + K)² + b
(X+K) + c = 0 |
|
Développons
le premier membre |
a
(X² + 2XK+ K²) + b X +b K + c = 0 |
|
|
a
X² + 2aXK+ aK² + b X +b K + c = 0 |
|
Mettons le terme en X en facteur commun |
a
X² + X (2aK+ b )+ aK² +b K + c =
0 (2) |
|
Déterminons K par la condition que le terme en X
soit nul |
2aK + b = 0
d’ où k = |
|
Remplaçons « K » par sa valeur dans
l’équation ( 2) |
a X² + |
|
|
a X² + |
|
|
a X² |
|
|
a X² = |
|
On cherche : « grand ixe »
= …….. |
X² = |
|
|
X = |
|
Puisque K
= X = On détermine
x = K + X |
x = |
|
Soit « petit ixe »
= |
x = |
Recherche des solutions permettant de résoudre les équations : suivant les valeurs dans l’équation de « a » ,
« b », « c » /
Trois cas
peuvent alors se présenter
Info traduction et lecture : x’ lire « ixe
prime » ; x ‘‘ lire « ixe
seconde »
Ces trois
cas sont :
1er cas : b² - 4 ac > 0
«x » a
deux valeurs distinctes ( que l’on nome « x
prime » et « x seconde »)
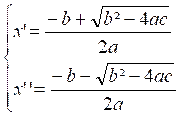
2e cas : b² - 4ac = 0
« x » a deux valeurs égales
x’ = x ‘’
= ![]()
3e cas : b² - 4 ac < 0
« x » n’a aucune valeur calculable.
Info :
l’expression b² - 4ac est appelée « discriminant », on la
représente par le symbole : Δ (delta)
En résumé : l’équation a x² +b
x + c = 0 a deux solutions distinctes , confondues ou
n’a pas de solution calculable suivant
que le discriminant est supérieur, égal ou inférieur à « 0 »
|
|
Simplification de la formule dans le cas ou
le coefficient « b » est pair ou plus exactement de la forme
« b = 2 b’ » |
|
Remplaçons « b » par « 2b’ » dans
la formule : x = 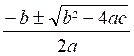
Ainsi : x
= 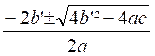 =
= 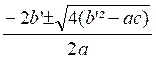
x
= 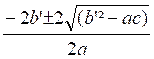
Soit en divisant les termes par
« 2 » : x = 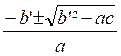
Cette formule est appelée « formule
réduite », l’expression « b’²-4ac » est
le discriminant réduit qu’on représente par Δ’.
Remarque :
Lorsque
« a » et « c » sont des signes contraires,
« 4ac » est négatif , « -4ac » est positif : l’équation a deux solutions distinctes.
Donc si
« a » et « c » sont de signes contraires l’équation a deux
solutions distinctes mais cette
condition suffisante n’est pas
nécessaire, « a » et « c » peuvent être de même signe et l’équation avoir deux
solutions distinctes.
Exemple : x² + 6 x - 112 = 0
Le coefficient
« b » étant pair , nous
utiliserons la formule réduite.
Identifions les coefficients : a = +1 ; b
= +6 ; c = - 112
Calcul du
discriminant : b’
² - ac = 9 +
112 = 121
Commentaire : Le discriminant étant positif , l’
équation a deux solutions distinctes :
Recherche des racines (solutions):
Racine carrée du
discriminant : ![]() = 11
= 11
Les racines ( solutions) de l’équation sont : x ’
= - 3 + 11 = 8 ;
x ‘’ = - 3 -
11 = - 14
|
|
3) Comment conduire la résolution
d’une équation du 2e degré. ? |
|
-
Il faut d’abord savoir reconnaître et résoudre les équations
incomplètes.
-
Il est conseiller de bien connaître les formes développées dans les identités
remarquables.
Autrement :
1) mettre l’équation sous la forme a x² + b x + c = 0
2) identifier les coefficients « a » , « b », « c » avec leurs
signes.
3) calculer le discriminant Δ = b² - 4 ac
( ou Δ’ = b’ - ac)
Commentaire : Si ce nombre était négatif le calcul
serait terminé , il n’y aurait pas de solution.
L’élève qui débute commet souvent une erreur de
signe dans le calcul du discriminant. Pour l’éviter il suffit d’utiliser le
moyen mnémotechnique suivant : on met « automatiquement » après
la quantité « b² » le signe - ou +, suivant que « a » et
« c » sont de même signe ou de signes contraires.
4) calculer la racine carrée de ![]() ou (
ou ( ![]() )
)
5) Appliquer les formules :
x ’ = 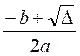 et
x ‘’ =
et
x ‘’ = 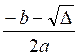
ou
x ’ = 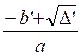 et
x ‘’ =
et
x ‘’ = 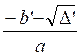
EXEMPLES DE RESOLUTION D’ EQUATIONS
|
Cliquer ici pour voir des exemples |
|
Soit la fraction |
Ici : vers Application : étude fonction ,recherche de limites…… |
|
Numérateur : résoudre et
factoriser : « x² + 2x – 8
= 0 » on obtient ( x – 2) ( x + 4) |
|
|
Dénominateur :
résoudre et factoriser :
« x² - 4 = 0 »
= …………..( x
– 2 ) ( x + 2) |
|
|
la fraction |
|
|
y = |
|
|
|
|
Pour INFO :
|
4°) L’ EQUATION BICARREE |
On appelle
« équation bicarrée » une équation du quatrième degré, ne renfermant
que des puissances paires de l’inconnue.
Une telle équation peut toujours être
« ramenée » à la forme :
(1) a x4 + b x² + c = 0
On résout facilement l’équation bicarrée par un
changement d’inconnue :
Nous
posons : x² = y
d’ où x = ![]()
L’équation (1) devient :
(2) a
y² + b y + c = 0 qui est une
équation de second degré en « y »
Dans le cas général , l’
équation (2) donne deux valeurs pour « y »
y
= 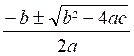
Soit quatre valeurs pour « x » :
y
= 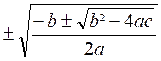
Exemple 1 :
x 4 - 25 x² +
144 = 0 (1)
d’ où x² =
y ; x = ![]()
L’équation (1) devient : y ² + 25 y + 144 = 0
Elle admet pour solutions : y’ = + 16
; y ‘ = + 9
D’ où x1
=
+ ![]() = +4
; x2 = -
= +4
; x2 = - ![]() = - 4 ; x 3 = +
= - 4 ; x 3 = + ![]() = +
3 ; x 4 = -
= +
3 ; x 4 = - ![]() = -
3
= -
3
Conclusion :
l’équation proposée admet quatre solutions.
Exemple 2 : x 4 - 12 x² - 64
= 0 (1)
d’ où x² =
y ; x = ![]()
L’équation (1) devient : y ² -
12 y + 64 = 0
Elle admet pour solutions : y’ = + 16
; y ‘ = - 4
D’ où x1
=
+ ![]() = +4
; x2 = -
= +4
; x2 = - ![]() = - 4 ;
= - 4 ;
Et :
|
x 3 = +
x 4 = +
|
Ces solutions ne sont pas calculables |
L’équation proposée n’admet que deux solutions
calculables.
Application : ( pour
celui qui veut se faire plaisir !!!)
Soit l’équation : ( 1 - x² ) L²ω4 - 2 ![]() ω² +
ω² + ![]() = 0
= 0
Dans laquelle ω , L , C , x sont des grandeurs essentiellement
positives ; ω est l’inconnue,
L, C sont connues , « x » est un paramètre.
Posons
ω² =
y ; ω
= ![]()
L’équation
proposée devient :
( 1 - x² ) L² y ² - 2 ![]() y +
y + ![]() = 0
= 0
Multiplions par C² : ( 1 - x² ) L² C² y
² - 2 L C y + 1 = 0
Identifions les coefficients :
a = (1 - x²) L² C² ; b =
- 2 L C ; b’ =
LC ; c = + 1
Calcul
de Δ ‘ : L²
C² - ( 1 - x²) L²C² = L²C² - L²C² + L²C²x²
Δ ‘ = L²C²x²
Calcul
de ![]() = L C x
= L C x
y ‘
=