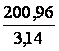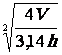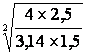|
Nomenclature 1 |
|
|
Factoriser la forme « ax2+b x +c » |
|
|
Forme canonique du "second degré" |
ENVIRONNEMENT du dossier:
DOSSIER : Résolution de l’ EQUATION du second degré «
complète » du type ax2+bx+c = 0
|
TEST |
COURS |
Interdisciplinarité |
|
|
Définition : |
Une équation du second degré à une inconnue est une
équation de la forme : ax2 + bx + c = 0
« x » étant l’inconnue et
« a » ; « b » ; « c » des données ,
remarque : « a »
étant différent de zéro ,sinon l’équation serait du premier degré.
Le premier membre de cette équation est la somme de trois termes :
« ax2 » est le premier terme du second degré.
« bx » est le second terme du premier degré.
« c » est le
troisième terme , appelé « indépendant de « x » ou « constant »
« a »
, « b » , « c » s’appellent les
coefficients
Rappels sur la
résolution de l ‘ EQUATION INCOMPLÈTE ( les coefficients sont
littéraux)
L’équation est dite « incomplète » si l’un des coefficient est
nul .Comme « a » est essentiellement différent de zéro, l’équation est
incomplète si « b » = 0 ou c = 0
Premier cas : b =
0
l’équation
s’écrit ax2 + c = 0
Elle est équivalente à : ax2 = - c ; x2 = ![]()
donc :
1°) si ![]() < 0 l’ équation n’a pas de
racine ; ( voir le nombre imaginaire)
< 0 l’ équation n’a pas de
racine ; ( voir le nombre imaginaire)
2°) si ![]() = 0 l’
équation a une racine x = 0
= 0 l’
équation a une racine x = 0
3°) si ![]() > 0
l’équation a 2 racines : x =
> 0
l’équation a 2 racines : x =
![]()
deuxième cas : c
= 0 , l’ équation s’écrit ax2 + bx = 0
ax2
+ bx = 0
en factorisant on obtient x
( ax + b ) = 0
elle se décompose et donne : x = 0
et ax + b = 0
c’est à dire
x = 0 et x
= -![]()
Remarque :
« Pratiquement » , pour
résoudre une équation du second degré incomplète , il ne faut pas utiliser ces
résultats littéraux , mais refaire le
calcul pour chaque équation considérée.
Fin du rappel.
Résolution d’une équation
complète ( les coefficients sont des nombres)
Nous savons résoudre certaines équations complètes d’une forme particulière .
I ) Ainsi , soit l’équation : ( x –2 )2
= 7
Cette équation se décompose en deux :
x
- 2 = ![]() et x-2 = -
et x-2 = - ![]()
par suite , elle admet deux racines :
x
=2 + ![]() et x = 2 -
et x = 2 - ![]()
On
écrit : x = 2 ± ![]()
II ) de même , pour résoudre l’ équation 4 ( x - 2)2 = 7
On écrira ( x - 2)2 = ![]()
x-2
= ![]()
x
= 2 ![]()
or , si nous développons ( x - 2)2 , l’ équation précédente : 4 ( x - 2)2
= 7
s’écrit : 4 x 2 –16x + 9 = 0
c’est une équation du second degré
« complète »
Pour résoudre une équation du second degré complète , nous pouvons la
mettre sous une forme analogue à « ( x - 2)2 = ![]() »
»
Exemple : résoudre l’ équation 2x2 + 9 x + 5 = 0
Divisons les
deux membres par 2 , on obtient : x2
+ ![]() x +
x + ![]() = 0
= 0
x2 + ![]() x est le commencement du développement du carré
de « x +
x est le commencement du développement du carré
de « x + ![]() x »
x »
( qui est
égal à x2 + ![]() x
+
x
+![]() )
)
nous écrirons
donc l’ équation précédente :
x2
+ ![]() x
+
x
+ ![]() -
-
![]() +
+ ![]() = 0
= 0
(
x +![]() )2 -
)2 -![]() =
0
=
0
(
x +![]() )2
=
)2
= ![]()
Par
suite on a :
Soit x +![]() =
= ![]() ; Soit x +
; Soit x +![]() = -
= -![]()
C’est
à dire : x = -![]() +
+![]() et x = -
et x = -![]() -
-![]()
On écrit x = ![]()
CAS GENERAL (Equation
à coefficients sont littéraux):
Afin d’examiner
tous les cas qui peuvent se présenter, nous procéderons comme dans l’exemple précédent avec
l’équation générale :
ax2 + b x + c = 0
« a », « b »
et « c » ne sont pas nuls.
En divisant les deux membres de l’équation par
« a » (qui est différent de 0 ) on obtient :
x2 + ![]() x
+
x
+![]()
ainsi : x2 + ![]() x est le
commencement du développement du
carré de
x est le
commencement du développement du
carré de
« x + ![]() » ;
qui est égal à x2 +
» ;
qui est égal à x2 + ![]() x
+
x
+![]()
nous écrirons donc l’équation
précédente :
x2 + ![]() x
+
x
+![]() -
-![]() +
+![]() = 0
= 0
( x + ![]() )2
-
)2
- ![]() = 0
= 0
on obtenons : ( x + ![]() )2 =
)2 = ![]()
le premier membre est un carré ; donc quel que
soit « x » , il est positif ou nul.
Nous sommes donc amenés à
distinguer plusieurs cas suivant que le second membre est positif ;
négatif ou nul. Comme le dénominateur ![]() est positif ; ces 3 cas sont :
est positif ; ces 3 cas sont :
|
b2 – 4ac < 0 |
|
|
b2 – 4ac = 0 |
|
|
b2 – 4ac > 0 |
|
|
b2 – 4ac < 0 |
Le deuxième membre est négatif ; donc
l’égalité ne peut pas avoir lieu et l’ équation « ax2 + bx + c
= 0 » n’a pas de racine.
Deuxième cas :
|
b2 – 4ac = 0 |
Le deuxième membre est nul et l’équation
« ( x + ![]() )2 =
)2 = ![]() »
s’ écrit : ( x +
»
s’ écrit : ( x + ![]() )2 = 0
)2 = 0
Ce qui donne : x + ![]() = 0
c’est à dire que x = -
= 0
c’est à dire que x = - ![]()
Donc , dans ce cas , l’ équation a une seule
racine : - ![]()
Troisième cas :
|
b2 – 4ac > 0 |
|
|
Le deuxième membre est positif.
L’équation «x + ![]() )2 =
)2 = ![]() »
se décompose en deux :
»
se décompose en deux :
x + ![]() = +
= + 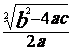 et x +
et x + ![]() = -
= - 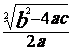
ce qui donne :
x = - ![]() +
+ 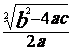 et x =
-
et x =
- ![]() -
-
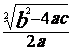
Donc dans ce cas
, l’ équation a deux racines :
x’ =![]() et x’’ =
et x’’ =![]()
on
écrit : x= ![]()
Conclusion.
On voit que l’équation a 0 ; 1 ou 2 racines suivants que b2 –
4ac est négatif , positif ou nul .
L’expression « b2 – 4ac » s’appelle
« le discriminant » de
l’équation « ax2 + bx + c = 0 » et on la représente par la
lettre ( delta) D
Ainsi :
D = b2 – 4ac
Les résultats que nous venons d’établir
s’énoncent :
RÈSUMÈ :
1 ° ) Si D
< 0
L’équation « ax2
+ bx + c = 0 » n’ a pas de racine
Commentaire : dans la représentation graphique
de cette équation la coupe ne
« coupe » pas l’axe des « x ».
2°) si D = 0 , l’
équation a une racine égale à -![]() ( appelée : racine double)
( appelée : racine double)
3°) si D > 0 , l’ équation a deux racines données par les
formules :
x=
![]()
remarque :
Les calculs
que nous faisons pour le cas
où D > 0 s’appliquent lorsque D = 0
.Dans ce cas , les deux racines x’ et
x’’ deviennent toutes deux égales à -![]() .
.
Pour cette raison , on dit que , lorsque
D = 0 , l’équation a deux racines ou une racine double .
Dans le cas où D >
0 , on dit que l’ équation a deux
racines distinctes.
Informations plus :
|
Forme
canonique de la fonction polynôme du
second degré. |
|
Si f(x) = ax2 + bx + c |
Avec a ¹0 |
RÈSOLUTION PRATIQUE :
Nous voyons que les calculs , pour résoudre une équation complète du second degré, sont longs.
Dans la pratique : On applique le théorème que nous venons de
démontrer en commençant par former D .
Ainsi faut-il connaître sans hésitation les résultats énoncés précédemment et
en particulier les formules : x= ![]()
Qui donnent les racines dans le cas où D est
positif .
Exemples :
|
I )
Résoudre l’équation : 2x2 + 5x + 9 = 0 |
INFO +++++ |
Calcul du discriminant
D = 25 –72 (= - 47)
D < 0 ; donc l’ équation n’a pas de racine .
|
II )
Résoudre l’équation : 3x2 + 7x + 1 = 0 |
INFO +++++ |
Calcul du discriminant
D = 49 –12 (= 37)
D > 0 ; donc l’ équation n’a deux racines
x =![]()
AUTRES REMARQUES :
Il existe
cependant des cas où il serait maladroit de procéder comme nous venons
de l’indiquer .C’est lorsque l’équation est mise sous forme d’un produit (P ) sous la forme P = 0 ; ou peut être mis aisément sous
la forme d’un produit de facteurs.
Exemples :
I ) résoudre l’équation ( 2x +1) ( 5x –3 ) = 0
L’équation se décompose en deux L un produit est « nul » si l’un des facteurs est nul )
Ainsi : ( 2x +1) 0 = 0 et 0 ( 5x –3 ) = 0
2x +1 = 0
et 5x –3 = 0
on a donc
immédiatement les racines :
x
= ![]() et x =
et x = ![]()
II ) résoudre l’équation :
( 3x-2 ) ( 4x-5) = (3x-2) ( 5x-2)
cette équation s’écrit :
(
3x-2 ) ( 4x-5) - (3x-2) ( 5x-2) = 0
on factorise :
(
3x-2 ) [( 4x-5) - ( 5x-2) ] = 0
(
3x-2 ) [ 4x - 5 - 5x + 2 ] = 0
(
3x-2 ) [ -x –3 ] = 0
l’équation
se décompose en deux :
3
x - 2 = 0 et - x –3
= 0
d’où les racines : x
= ![]() et x
= 3
et x
= 3
III ) Résoudre l’équation :
( 2x-3)2 = ( 5x + 8)2
Cette équation s’écrit ( 2x-3)2 -( 5x + 8)2 =
0 ( voir les I.R. )
( 2x – 3 + 5 x
+ 8 ) (2x – 3 – 5 x – 8 ) = 0
( 7 x + 5 ) ( - 3 x – 11) = 0
d’où les racines : x = ![]() et x
=
et x
= ![]()
autre remarque N°2 :
Soit l’équation 2x2-4x –5 = 0 dans
laquelle « a » et « c » sont de signe différent le produit « ac » est négatif . Le D = b2-4ac
s’obtient en retranchant de b2 qui est positif un nombre négatif.
Cela revient à lui ajouter un nombre positif . Le résultat est donc positif.
Par suite :
Si dans une équation du second degré : ax2 + bx +
c = 0
« a » et « c » sont
de signe différent ont peut affirmer que l’équation a deux racines distinctes.
autre remarque N°3.
Si le coefficient « b » se présente sous la forme 2b’ on a :
D = b2 – 4ac = 4 b’2 – 4ac = 4 (b’2
– ac)
au lieu de former D , on
peut donc former l’expression D’ = b’2 – ac qui
a le même signe .
D’ ( lire delta prime) s’appelle le discriminant réduit de
l’équation .
si D’ < 0 , l’équation n’a pas de
racine ;
si D’ = 0
, l’ équation a une racine : x =![]()
si D’ > 0 , l’ équation a deux racines données par les
formules :
x = 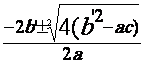
ou x = 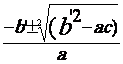
COMPARAISON DES RACINES .
Lorsqu’une équation du second degré a deux racines distinctes x’ et x’’ , quelle
est la plus grande ?
Nous avions trouvé :
x’ =![]() et x’’ =
et x’’ =![]()
en écrivant
x’ = - ![]() +
+ ![]() et x’’
= -
et x’’
= - ![]() -
-
![]()
On voit
que :
si a > 0 on a :
x’ > x’’
si a
< 0 on a x’ < x’’
TRAVAUX AUTO
FORMATIFS :
EVALUATION
Résoudre l’équation : y
= x2 – 4 x + 3
AIRE
d' un CARRE:
|
A = c 2 |
A = aire |
c = longueur d' un coté |
Problème
1:
Calculer le coté d'un carré de
|
225 cm2 = c 2 |
D'ou c = |
C = + ou -
Conclusion : le coté du carré vaut La solution négative ne peut convenir. |
Problème
2
Calculer le rayon d'un disque dont on connaît son
aire:
|
A = 200,96 cm2 |
A = 3,14 R2 |
|
Donc 200,
96 = 3,14 r2 |
Après transformation R2 = 64 |
|
R = |
R = |
Problème
3
Quel diamètre convient-il de donner à un cylindre de
|
25 hectolitres |
25 |
25 00 décimètres cubes |
2 , |
|
Le volume d'un cylindre: V = |
|
|
4V = 3,14 D2h |
D2 = |
|
|
D = |
|
|
D = |
Le
mouvement uniformément varié