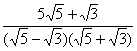Les IDENTITES REMARQUABLES de la forme : (A + B ) ( A - B )

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

>>>Info générales.

>>>Aide pédagogique

COURS

La forme ( a + b ) ( a - b ) s’écrit aussi ( a - b ) ( a +b )

Exemples : ( x +1 ) ( x - 1 ) qui s’écrit aussi ( x -1 ) ( x + 1 )

( 3x + 2 ) ( 3x - 2 ) qui s’écrit aussi ( 3x - 2 ) ( 3x + 2 )

La forme fondamentale : ( a + b ) ( a - b ) = a² - b² est utilisée Développement de ( a + b ) (a - b ) soit la forme factorisée a² - b ²

(voir page 7 objectif : FACDEVE)

Recherche de la forme développée:

( a + b ) (a - b) , on met un indice à « a » et « b »

ce qui donne :

( a₁ + b₁ ) ( a₂- b₂) = ? se souvenir que (a₁= a₂et b₁ = b₂)

on transforme les soustractions en additions .

(se souvenir qu une soustraction se transforme en addition à condition de respecter la régle : on ajoute au premier nombre l’opposé du second )

( a + b ) ( a - b ) = ( a₁ + b₁ ) ( a₂ + (- b₂))

Développement :

( a₁ + b₁ ) ( a₂ + (- b₂)) = a₁ a₂+ a₁ (-b₂)+ b₁ a₂+ b₁(- b₂ )

On effectue le calcul pour chaque terme (avant de regrouper )

(voir objectif sur les décimaux relatifs: Obj: D....)

se souvenir que (a₁= a₂et b₁ = b₂)

a₁ a₂= a a = a²

a₁ (-b₂) = ( - a₁b₂ ) = - ab

b₁ a₂ =ba = ab

b₁ (- b₂ ) = - b₁ b₂ = - b b =- b²

on réécrit l’égalité:

( a + b ) ( a - b ) = a² + (- ab ) + ab + (- b²)

-ab +ab = 0

( a+ b ) ( a - b ) = a² + 0+ (- b²)

( a+ b ) ( a - b ) = a² - b²

ON RETIENDRA :

( a +b ) (a -b) = a² - b²

Traduction en langage littéral :

Le produit de la somme de deux nombres par la différence de ces deux nombres est égal à la différence des carrés de ces nombres .

la Quantité ou expression conjuguée :

Info +@

Rappel : On dit qu’une expression numérique est « irrationnelle » lorsqu’elle renferme des radicaux portant sur des nombres qui ne sont pas des carrés parfaits. Sinon l’expression est « rationnelle ».

Lorsqu’on veut calculer une valeur décimale approchée d’une expression numérique irrationnelle dans laquelle il y a des radicaux en dénominateur, on a intérêt (afin d’avoir à effectuer des divisions plus courtes) à trouver une expression égale qui n’ait pas de radicaux au dénominateur. On dit que l’on chasse les radicaux du dénominateur. ( @ les quantités conjuguées)

II) pour rendre rationnel les dénominateurs de fractions contenant des radicaux tel que :

ou ; ou ou bien encore ;ou alors

il faut multiplier le numérateur et le dénominateur par la Quantité ou expression conjuguée :du dénominateur

nous conviendrons d’appeler l’expression ( a + b ) ( a - b ) ; « expression conjuguée » :

Une expression conjuguée est un produit de deux facteurs chacun contenant deux termes leur premier terme étant identique( a),leur second terme étant opposé ( « +b » et « -b » ).

Exemples :

par définition nous dirons que les expressions : et sont dites « conjugués »

il suffit de faire le produit de ces expressions conjuguées ,le résultat sera entier ou décimal (les radicaux auront disparus ........)

nous savons par ailleurs qu’une fraction reste « équivalente » si l’on multiplie le numérateur et le dénominateur par un même nombre (ou expression même conjuguée) ,si nous voulons faire disparaître au dénominateur d’une fraction une expression contenant un radical il suffira de multiplier le numérateur et le dénominateur par l’expression conjuguée du dénominateur !

Ainsi : si on a à calculer les valeurs décimales approchées des nombres et on les écrira au préalable :

	= =
	= =

EXERCICES TYPES :

Pour chaque exercice , il y a deux solutions:

Première solution

on applique directement : ( a +b ) (a -b) = a² - b²

on pose a = x et b = 1 ;

Deuxième solution:

on transforme ( a + b ) ( a - b ) en ( a₁ + b₁ ) ( a₂ + (- b₂))

Dans ce cas on pose a = x et (- b) = (-1 )

et l’on développe ................

Dans les exemples qui suivent la première solution sera retenue:

A ) Développer : ( x +1 ) ( x - 1 )

on applique : ( a +b ) (a -b) = a² - b²

(x +1 ) (x - 1 ) = x² - 1²

On calcule pour chaque terme :

a² =x fois x = x²

b ² = 1² = 1

(x - 1 ) ² = x² -1

B) Développer : ( 3x + 2 ) ( 3x - 2 )

on applique : ( a +b ) (a -b) = a² - b²

On pose a = 3x et b = 2 ; : ( 3x + 2 ) ( 3x - 2 ) = ( 3x )² - 2²

On calcule pour chaque terme:

a² = (3x)² = 9 x²

b² = 2² = 4

Conclusion: ( 3x + 2 ) ( 3x - 2 ) = 9 x² -4

Factoriser : a² -b²

Nous savons que la forme a²-b² est la forme développer de (a + b ) (a - b ) ; nous pouvons conclure que la forme factoriser de a² -b² est (a + b ) (a - b ).

Exercice type :

Factoriser: 9 x² - 4

Procédure: (de factorisation)

a )On reconnaît un polynôme du second degré (grâce au « x² » )

b) On remarque que ce polynôme contient deux termes ,dont pas de terme « x » de degré 1 mais un terme « négatif », il pourrait être de la forme a²-b²

c) Nous allons comparer terme à terme , pour vérifier si ce polynôme peut se mettre sous la forme ( a+b)(a-b); dont la forme développée est a²-b²

1 ) Est ce que 9 x² est de la forme a² ?

CONVENTION D’ECRITURE :

Dans l’expression (a - b ) ² ; 9 x² est de la forme « a² » est non de la forme « b² » ; parce que « le terme en « x » de chaque facteur est « en tête » , donc suivi du signe « - »

On utilisera toujours cette écriture (x+ b ) ( x - b ) au lieu de (a + x ) ( a -x )

9 est le carrée parfait de 3 on peut écrire 9x² = 3² fois x² ,

( se souvenir que le carré d’un produit est égale au produit des carrés (et inversement le produit d’un carré est égal au carré des produits : 3²x² =( 3x )² )

on peut conclure que 9x² est de la forme a² ; soit ( 3x )²

3) Est ce que « 2 » convient pour « b » ?

On sait que b²est égale à 4 ,que racine carrée de 4 vaut 2 , donc « b » à pour valeur « 2 »

d) Inventaire des calculs:

puisque a² = ( 3x )² que b = 2 ;donc que b² =4

e) Conclusion:

9 x² - 4 est de la forme a²-b² ; avec a=3x et b=2

donc la forme factorisée de 9x² -4 = ( 3x+ 2) ( 3x- 2)

Réponse la factorisation de 9x² -4 est ( 3x+ 2) ( 3x- 2)

Certains polynômes du second degré ne peuvent se factoriser de façon « directe » tel :

x² + 1 ; x²-77 ; 2x²-21 ;........................

Nous trouverons une solution ,quand elle existe , d’opérer une factorisation lorsque nous aborderons l’objectif traitant de l’équation du second degré. « EQUA2° »

APPLICATION

Données du problème :

Un rectangle a pour aire : ........................

Sa longueur est de : x +

Sa largeur est de x + ...

Questions :

Calculer « x »

Calculer sa longueur et sa largeur:

CONTROLE:

Donner la forme mathématique du développer d ‘une somme de deux nombres par la différence de ces deux nombres.

EVALUATION.

I ) Développer:

(3x+1) (3x-1)=

( x+1 ) ( x -1 ) =

(x +3 ) (x -3 ) =

(x +) ( x - ) =

(x +1) (x -1) =

II ) Factoriser:

x ²- 36

16x² - 9

III ) Que faut-il ajouter aux expressions suivantes pour les transformer en carré d’une différence ?


a² + b²
9a² - b²
4a² - 4b²
a² - b²
a² -9b²

DEVOIR BILAN:

Factoriser les expressions suivantes:

(il est nullement question ici de chercher à résoudre une équation ,ni même d’étudier une fonction ;il est simplement demandé de trouver une nouvelle forme d’écriture mathématique)