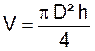Pré requis:
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif précédent : 1°) Résoudre une équation incomplète ou complète du second degré. |
|
Retour vers la liste des cours sur le second degré
« équations » |
DOSSIER : le second degré : Suite : Série 2 : EXERCICES et PROBLEMES du second degré.
|
|
|
|
2°) Résolution des problèmes du second
degré.(définition et procédure) |
|
|
|
|
TEST |
COURS
|
|
|
I ) Rappel . |
|
Rappel : par
définition une équation à une inconnue est dite du second degré, lorsque après
avoir fait toutes les réductions possibles , elle
renferme l’inconnue « au carré ».
Equation type : 5 x²
- 75 = 0
Nous en déduisons
successivement :
5 x² = 75 ; x² = (75
/ 5) ; x² = 25
Extrayons les racines
carrées des deux membres de l’équation
![]() soit x = ± 5
soit x = ± 5
nous aurons deux
solutions : 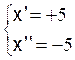
En
effet : ( +
5 ) ² = + 25 et ( - 5
) ² = + 25
1°) Trouver deux
nombres sachant que leur différence est 12 et la somme de leurs carrés 1530.
Résolution :
Choix de
l’inconnue : soit « x » le plus petit des deux nombres, l‘autre sera
« x+12 »
Mise en
équation :Leurs carrés sont « x² » et
« x² + 24 x + 144 ».
On doit donc
avoir : x² + x² + 24 x + 144
= 1530
Ou 2 x²
+ 24 x - = 1530
|
|
|
|
Série 1 :
a) Carré (@):
1) S =
c² ; S = aire, c = côté
Problème : calculer le côté d’un carré de
225 centimètres carrés d’aire.
c² = 225 , d’où c = ± ![]() = ± 15
centimètres ;
= ± 15
centimètres ;
c = 15 centimètres
la solution négative ne convient pas au problème.
2) Calculer le côté d’un carré qui soit le ![]() d’un carré de 24
centimètres de côté. (au mm près)
d’un carré de 24
centimètres de côté. (au mm près)
S = 24 ² =
576 , S’ = (576 : 6) = 96
C² = S’ ; c² = 96 d’où
c = ![]() ; c "H 9 , 708
.cm =
98 mm
; c "H 9 , 708
.cm =
98 mm
Série 2
1° Problème d’arithmétique : Si du carré d’un nombre, on retire 24 unités , on obtient 120 unités. Calculer ce nombre.
Solution :
1°) Soit « x » le nombre
demandé
2°) mise en équation :*
x² - 24 = 120
3°)résolution de
l’équation :
x² = 120
+ 24
x² = 124
x = ![]() ou x = ± 12
ou x = ± 12
4°) On voit qu’on obtient deux
réponses : une positive te une négative.
c’est qu’en effet, le carré de -12
est 144 ,
et le carré de +12 est aussi 144.
Remarque :
dans ce problème, les deux réponses s’admettent. D’autres problèmes n’admettent
que la solution positive.
Problème 2 ( de géométrie) :
Un champ rectangulaire a pour surface 4 800 mètres
carrés. Sachant que la longueur est le triple de sa largeur, on demande de
calculer ses deux dimensions.
Solution :
On posera l’équation de la surface d’un
rectangle. Soit « x » la largeur , on aura
comme longueur « 3x » , et l’on écrira :
3x × x = 4 800
3 x²
= 4 800
x ² = 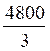 = 1 600
= 1 600
x = ![]()
x = ± 40
Dans ce cas : la réponse positive
est seule admissible.
Calculer le
diamètre du cercle de même surface
qu’une calotte sphérique de 30 millimètres
de hauteur et de 750 mm de diamètre de sphère. (voir figure ci dessous)
Soit « x » le diamètre du cercle cherché,
sa surface est ![]() .nous avons vu en géométrie que la surface de la calotte est « S = 2 À R h » ou « S = À D h »
.nous avons vu en géométrie que la surface de la calotte est « S = 2 À R h » ou « S = À D h »
Donc nous aurons : 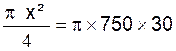
Nous divisons les deux membres par « À » , nous aurons :
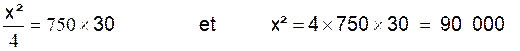
d’
où ![]() = 300 millimètres.
= 300 millimètres.
Problème n°3 :
Rappel : la pression « p » due à une force
pressante de valeur F perpendiculaire à la surface de contact « S » est donnée
par :
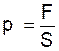
avec « p » exprimée en pascal
(Pa) ; « F » en newton (N) et « S » en mètre carré ( m²)
* l’unité de pression est le pascal (Pa) : 1 Pa = 1 N. m-2 , dans la pratique , on utilise le bar ( bar) : 1
bar = 105 Pa
Quel diamètre convient -
il de donner à une barre de fer rond
devant supporter un effort longitudinal de 7 0 000 newtons , le coefficient de résistance étant de 700
bars soit 70 000 000 pascals ?
( g = 10 )
F = 70 000 N
; p = 70 000 000 Pa ( 700 bars)
Nous avons vu en science que F = p S et par suite :
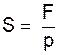 ;
; 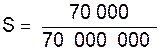 = 0 , 0010 mètre
carré soit 10 cm² .
= 0 , 0010 mètre
carré soit 10 cm² .
Nous avons donc
: 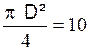
D’où :
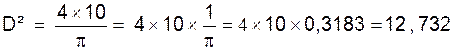
Et :
![]() = 3,56. cm =
35, 6 .mm
= 3,56. cm =
35, 6 .mm
Problème :
Cylindre.
|
|
V =
volume ; D =
diamètre ; h = hauteur . |
Quel diamètre convient- il de donner à un cylindre
de 1,50 .m de haut pour obtenir une capacité de 25 hectolitres ?
On sait que ( @ ) 25 hectolitres = 2500 litres = 2500
décimètres cubes = 2,500 m3
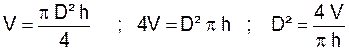
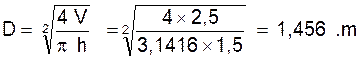
problème :
sur le Mouvement
uniformément varié .
|
|
v =
vitesse vo
= vitesse initiale e =
espace parcouru. ³ = accélération du mouvement. |
Info : « sciences »
Si le corps part au temps t0 ( repos)
; v 0 = 0 et les
formules deviennent « v =
at » et « 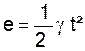
Problème : Au départ d’une gare un train
met 40 secondes pour atteindre, sa vitesse uniforme de 72 kilomètres à l’heure , pour s’arrêter ,il ralentit sa vitesse de 0,40 .m
par seconde. On demande :
1°) l’accélération du mouvement de départ.
2°) l’espace parcouru quand il atteint sa vitesse
normale.
3°) le temps qu’il lui faut pour s’arrêter.
4°) la distance de la gare d’arrivée à laquelle le mécanicien doit stopper
l’alimentation en électricité du moteur.
1°) 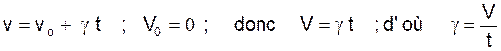
« t » est en seconde » alors par
convenance on déclame la vitesse ( V ) en m /
s : v = 72 kilomètres à l’heurs ou 72 000 mètres
en 3600 secondes soit
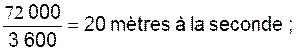 (
20 m /s)
(
20 m /s)
donc 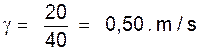
2°) 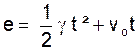
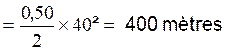
3°) ![]() de cette formule
nous tirons :
de cette formule
nous tirons : 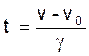
mais « v = 0 » correspondant à l’ arrêt ; v0 = vitesse initiale 72
kilomètres à l’heure ou 20 m /s ; ³ = - 0,40
.m/s accélération décélérée. (dit aussi : retardatrice)
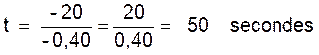
4°) 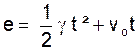 ;
; 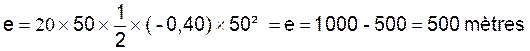
Problème :
On demande combien de coups par minute on pourrait
faire battre à un mouton de casse - fonte tombant d’une hauteur de 8 mètres,
s’il faut 10,72 secondes pour le remonter après chaque chute.
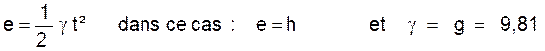
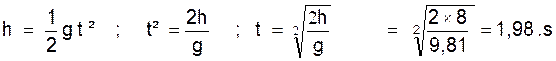
Temps de chute + temps de remontée = 10,72.s + 1,98
.s = 12 .s
Nombre de coups par minute : 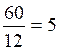
Problème
Un corps est lancé verticalement de bas en haut avec une vitesse initiale de 30 mètres à la
seconde. On demande :
1°) Le temps de la montée.
2°) la hauteur qu’il atteindra.
3°) le temps de la chute .
4°) la vitesse quand il arrivera au bas de sa
chute. (On ne tiendra pas compte de la résistance de l’air.)
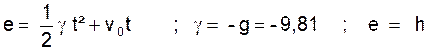
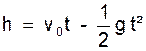
1°) Quand le corps s’arrêtera la vitesse sera nulle ; or ; v = v0 - gt = 0
donc 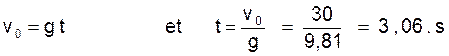
2° ) 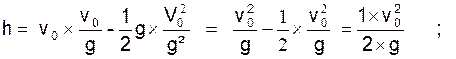
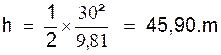
3°) 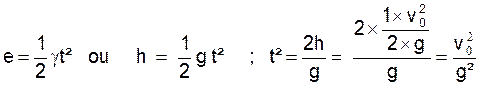
d’où 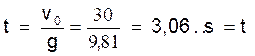
Nous voyons que la durée de la chute est la même
que celle de la montée.
4°) v’ =
v ‘0 + gt ; v’0 = 0
v’ =
g t =
v0 = 30 mètres.
La vitesse à l’arrivée au sol est la
même que la vitesse de départ.
Puissance vive d’un
corps en mouvement .
Problème : un corps tombe dans un puits de
mine de 50 m de haut . Quelle est sa vitesse en
arrivant au sol ?
Nous avons
v² = 2 g h d’où
![]()
|
B) |
EQUATION COMPLETE |
|
Problème: Un rectangle a des côtés égaux respectivement à 4 m et 7 m . De combien doit - on augmenter l’un des côtés pour que , en diminuant
en même temps l’autre côté de la même longueur, l’ aire de la surface deviennent 24 mètres carrés.
Si l’on désigne par « x » la longueur
cherchée, exprimée en mètres, les côtés deviendront respectivement « 4 + x » et « 7
-x » ; si « x » est positif , on aura augmenté le côté égal
primitivement à « 4 » et diminué l’autre ; si « x »
est négatif , ce sera le contraire , mais en tout cas les conditions de l’énoncé
sont satisfaite. L’aire de la surface d’un rectangle exprimée en mètres carrés
est égale au produit des côtés exprimés en mètres ; on doit donc
avoir :
( 4 + x ) ( 7 - x ) = 24
c’est à dire x ² - 3 x - 4 = 0
d’où l’on tire : x = 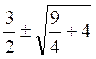 =
= 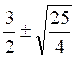 =
= 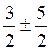
On a deux racines x ‘ = ![]() = 4
= 4
x’’ = ![]() = - 1
= - 1
Commentaire : la première donne pour côtés
« 4 + 4 » et « 7 - 4 » c’est à dire « 8 » et « 3 ». On a donc
deux solutions du problème proposé , mais ces
solutions conduisent à deux rectangles égaux, dont les côtés sont simplement
permutés. Cela tient à ce que le problème proposé revient à ceci : puisque
l’on diminue l’un des côtés , et qu’on augmente
l’autre de la même longueur , leur somme
reste constante et égale à « 11 »,il s’agit donc de trouver un
rectangle connaissant la surface et la moitié du périmètre ; nous allons
résoudre ce problème et voir qu’l y a un seul rectangle répondant à la
question.
Problème 4 : Quels sont les côtés d’un rectangle dont on connaît l’aire « 30 mètres carrés » et le périmètre « 22 m. »
Désignons par « x’ » et « x’’ » ses côtés, exprimés en
mètres, le périmètre est « 2 x’+ 2 x’’ » et l’aire « x’
x’’ » ; on a donc :
2x’ +
2x’’ = 22 soit
x’ + x’’ = 11
et x’ x’’ = 30
il s’agit donc de trouver deux nombres
« x’ » et « x’’ » connaissant leur somme et leur
produit. Pour cela, nous remarquerons que nous connaissons les coefficients de
l’équation du second degré qui admet pour racines « x’ » et
« x’’ » ; cette équation est :
x²
- ( x’ + x’’) + 30 = 0
Nous pouvons la résoudre, ce qui donne :
X = ![]() ±
± 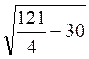 =
= ![]() ±
±
![]()
Les deux racines sont « 5 » et
« 6 » ; on peut donc prendre, ou bien :
x’
= 5 et
x ‘’ = 6
ou bien : x’ =
6 et
x ‘’ = 5
Conclusion : On a deux solutions, mais à ces deux solutions correspondent deux
rectangles égaux ; leurs côtés seuls sont intervertis.
Problème 5 : Trouver deux nombres dont la
différence soit « 3 » et le produit « 40 ».
Nous allons ramener le problème au précédent ;
dans ce but, nous remarquerons que la différence de deux nombres est égale à la
somme du premier et d’un nombre opposé au second ; nous sommes ainsi
conduits à désigner le premier nombre par « x’ » et le second par
« -x’’ » ; leur différence est alors « x’ + x’’ » et
leur produit est « - x ’x’’ » ; on a ainsi les deux
équations :
x’ + x’’ = 3
x’ x’’ = - 40
Donc
« x’ » et « x’’ » sont les racines de
l’équation : x² - 3 x - 40 = 0
D’où l’on tire :
x = ![]() ±
± 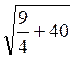 =
= ![]() ± . =
± . = ![]() ±
±
![]()
les deux racines sont « 8 » et « -5 » ; on peut
prendre :
x’ = 8 et x’’
= -5
donc les deux nombres « x’ » et « -x’’ » sont
« 8 » et « 5 » On peut prendre aussi :
x’ = - 5 et x’’
= + 8
Donc les deux nombres « x ‘» et « -x’’ » sont -5 et - 8
On a ainsi deux solutions à la question posée.
TRAVAUX
AUTO FORMATIFS.
1° ) Combien de termes
composent une équation du second
degré ?
2 °) Comment nomme –t-on son premier membre ?
3°) Dans le premier membre comment nomme
–t-on :
Le premier
terme ?
Le second
terme ?
Le dernier
terme ?
Et encore :
1. Qu’est ce qu’une équation ?
2. Qu’entend -
on par résoudre une équation ?
3. Qu’appelle t - on degré d’une équation ?
4. Enoncez la règle pour résoudre une équation du premier degré à une inconnue ?
5. Quand on fait passer un terme d’une équation d’un membre dans un autre
quelle précaution doit -on prendre ?
6. Enoncez la règle pour résoudre un système de deux équations à deux
inconnues par la méthode de substitution ?
7. Qu’appelle - t-
on équation du deuxième degré à une inconnue ?
8. Donnez les solutions x’ et x’’ de
l’équation générale « a x² + b x +
c = 0 »
|
Identifier les membres et nommer les termes : |
|
|
1°)
Dans l’équation : - 3x – 1 + x2 = 0
|
|
|
2°)Dans
l’équation : + x2 – 1
= 0 |
|
|
3°) ( m + 3 ) x2 – ( 2 – n + p )x + m – n
= 0 |
|
Exercices de
récapitulation :
Ordonner les polygones suivants :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculer les
surfaces suivantes données par les formules Lexprimer toutes les quantités à
l’aide de la même unité)
INTERDISCIPLINARITE :
Problème 1 : Un brocanteur achète une caisse contenant un lot
« soldé » de vases en verre blanc pour 360 € , 3 sont cassés et vend
les autres 5 euros de plus par vase qu’ils ne lui ont coûté. Il gagne ainsi 15
euros sur son marché ; combien chaque vase
lui avait-il coûté ?
Solution : soit « x » le
nombre de vases ; chaque vase lui coûte ![]() ;
il en pers 3 , donc il lui en reste « x - 3 » ; il revend
chacun 5 € de plus par vase , on il en revend chacun «
;
il en pers 3 , donc il lui en reste « x - 3 » ; il revend
chacun 5 € de plus par vase , on il en revend chacun « ![]() +
5 » ; cela fait ( x - 3)
(
+
5 » ; cela fait ( x - 3)
( ![]() +
5 )
+
5 )
Et ainsi
il gagne 15 euros , il doit donc toucher 360 + 15 ou 375 € .
On a enfin : ( x
- 3) ( ![]() +
5 ) = 375
+
5 ) = 375
Soit
5x² - 30x - 1080 = 0 ou
x² - 6x - 216 = 0
Les racines sont « 18 » et
«-12 » ; le nombre « 18 » répond seul à l’énoncé
proposé ;le nombre « -12 » satisfait à
un énoncé modifié.
Problème 2 :
Deux ville « A » et « B » sont situées sur un
fleuve ;« A » à 42 km en aval de
« B ».Un bateau fait le service entre les deux villes. Sachant que la
vitesse du courant est de 4 km/h et que
la différence des trajets « AB » et « BA » est de 1h 12
min. Calculer la vitesse du bateau.
1°) choix de l’inconnue : soit
« x » la vitesse propre du bateau.
2°) Mise en équation : Admettant que
la vitesse réelle du bateau est égale à sa vitesse propre ,
augmentée ou diminuée de la vitesse du courant suivant qu’il le descend (trajet BA)
ou qu’il remonte ( trajet AB) nous exprimerons algébriquement
l’égalité :
Durée du trajet AB -
durée du trajet BA = 1 h ![]() ou
ou ![]() h .
h .
![]() -
- ![]() =
= ![]()
3°) Résolution de l’équation :
![]() -
- ![]() =
= ![]()
Supposant x¹ 4
et x ¹ -4
Multiplions tous les termes par le p.p.d.c. qui est : 5 ( x+ 4)
- 42 ( x -4) = 5 ( x² - 16)
il
vient : 210 ( x - 4) - 210 (
x- 4 ) = 6 ( x² - 16 )
soit 210 ( x + 4 - x + 4 )
= 6 x² - 96
1 680 = 6 x² - 96
6 x² = 1 680 + 96
= 1 776
x²
= ![]() = 296
= 296
x
= ± ![]() = ± 17,2
= ± 17,2
4°) Discussion : seule la réponse positive convient :la vitesse propre du bateau est de 17,2 km / h .
Problème 3 :
Une amicale d’anciens élèves organise une excursion
en autocars. Le prix global de l’excursion s’élève à 1200 €. Le nombre des
participants étant supérieur de
« 4 »au nombre prévu chacun peut ainsi payer 10 € en moins. Quel
était primitivement le nombre d’excursionnistes ?
Solution :
1°) Choix de l’inconnue : soit
« x » le nombre d’excursionnistes.
2°)Mise en
équation :
Nous exprimerons algébriquement
l’égalité :
« part de chaque excursionniste ans le 1er
cas » = « part de chaque excursionniste dans le second cas + 10
€ »
soit ![]() =
= ![]() + 10
+ 10
3°) Résolution de l’équation :
![]() =
= ![]() + 10
+ 10
Supposant x ¹ 0 et x ¹ - 4 multiplions tous les termes par le p.p.d.c.:
« x ( x+4) »
![]() =
= ![]() + 10
devient 1200 (
x + 4) = 1200x + 10 x (x+4)
+ 10
devient 1200 (
x + 4) = 1200x + 10 x (x+4)
1200
x + 4800 = 1200x + 10 x² + 40 x
10 x² + 40 x - 4800 = 0
Soit en simplifiant : x² + 4 x - 480 = 0
« a » = +1 ; « b » = + 4 ;
« b’ » = +2 ; « c » = - 480
” = 4 + 480 = 484
![]() = 22
= 22
« x’ » = -2 + 22
= + 20
« x ’’ » = - 2 - 22
= - 24
4°) discussion : la solution positive convient seule. Le
nombre des excursionnistes primitivement prévu était de « 20 ».
Problème 4 :
Un ascenseur monte dans une cage d’escalier à la vitesse constante de 2
mètres par seconde.
Quand il a parcouru 10 mètres, on abandonne, à 20
mètres du bas de la cage une pierre qui descend avec une accélération de 9,80
mètre à la seconde par seconde. A quelle distance du haut de la cage , la rencontre se produira - t- elle ?.
Voir dessin niveau « 0 » départ de
l’ascenseur vers le haut,la
pierre est au niveau (+20) ;quand l’ascenseur est au niveau (+10), la
pierre est lachée.
Solution : En premier lieu
nous remarquerons que le mouvement de la
pierre étant uniformément accéléré ( @ ) , son équation
est :
e =
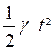 avec « e » l’espace parcouru ;
« ³ » l’accélération ; « t » durée de parcours.
avec « e » l’espace parcouru ;
« ³ » l’accélération ; « t » durée de parcours.
Le mouvement de l’ascenseur étant uniforme,
son équation est :
e = v t avec « e » l’espace parcouru ;
« v » la vitesse ; t la durée du parcours.
1°) Choix de l’inconnue : soit
« t » la durée de la chute de la pierre exprimée en secondes.
2°) Mise en équation :
Nous exprimerons algébriquement
l’égalité :
« Chemin parcouru par l’ascenseur +
chemin parcouru par la pierre = 20 m »
10 + 2t + 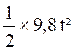 = 20
= 20
3°) résolution de l’équation :
10 + 2t + 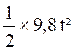 = 20 devient 4,9 t² + 2 t - 10 = 0
= 20 devient 4,9 t² + 2 t - 10 = 0
« a » = + 4,9 ;
« b » = +2 ; « b’ » = +1 ;
« c » = - 10
” = 1 + 49 = 50
![]() # 7,07
# 7,07
t’ = 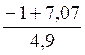 # 1,25 s
# 1,25 s
t’’
= 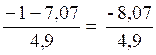 s Cette réponse négative ne peut convenir.
s Cette réponse négative ne peut convenir.
La distance du point de rencontre au haut
de la cage s’obtient en remplaçant dans la formule « e = 4,9 t² » , « t » par sa valeur « 1,25 ».
On
trouve « e #
7,65 m”
Problème 5 : Un détaillant en électroménager ayant commandé des lampes de
bureau pour une somme de 4375 € constate une erreur à la livraison. Le
fabriquant lui a expédié des lampes valant 3,75 € de moins par unité mais leur
nombre est supérieur de 15 au nombre de lampes commandées. Le détaillant
conserve la livraison pour le prix convenu. On demande quel était le nombre de
lampes commandées et le prix d’une lampe.
Solution :
1°) Choix des
inconnues : soit « x » le nombre de lampes commandées et
« y » le prix d’une lampe.
2°) Mise en équations : nous
exprimons algébriquement les égalités :
(1) le prix total des lampes dans le 1er cas est 4375 €
(2) le prix total des lampes dans le 2e cas est 4375 €
d’où le
système 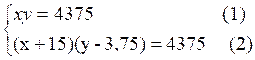
3°) Résolution du système
Dans l’équation (2) effectuons les
parenthèses et réduisons
x y - 3,75 x + 15 y - 56,25 = 4375
x y - 3,75 + 15 y = 4 431,25 (2)
de l’équation (1) tirons la valeur de « y » : y = 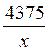
Remplaçons « y » par son valeur
dans l’équation (2)
x × 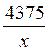 - 3,75 x + 15 ×
- 3,75 x + 15 × 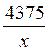 = 4431,25
= 4431,25
Soit
- 56,25 - 3,75 x + 15 × 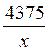 = 0
= 0
« x » n’étant pas nul
multiplions tous les termes par
« x »
- 56,25 x - 3,75 x² +
65 625 = 0
ou 3,75 x² + 56,25 x - 65 625 = 0
« a » = + 3,75 ;
« b » = + 56,25 ; « c » = - 65625
” = 3164,0625 + 984375 =
987539,0625
![]() = 993,75
= 993,75
x’ = 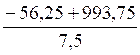 = 125
= 125
x’ = 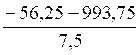 = - 140
= - 140
4°) Discussion : la réponse positive
x’ = 125 convient seule.
Reportons cette valeur dans l’égalité
« y = 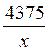 » nous obtenons
« y =
» nous obtenons
« y = 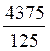 =35 »
=35 »
Le nombre des lampes de poche
commandées était de 125 et leur prix unitaire de 35 €.