Les Fonctions numériques

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent Cours complet sur l’étude d’une fonction numérique .

Objectif suivant INFO PLUS sur l’étude des fonctions.

tableau 1°) Le second degré niveau V BEP 2°) Les tracés BEP

DOSSIER : N°1 Etudes des FONCTIONS NUMERIQUES

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Exemples de f : R R	Nom de fonction	Info++
x ax	Fonction linéaire
X ax + b	Fonction affine
X x^2	Fonction monôme du second degré
X x^3	Fonction monôme du troisième degré
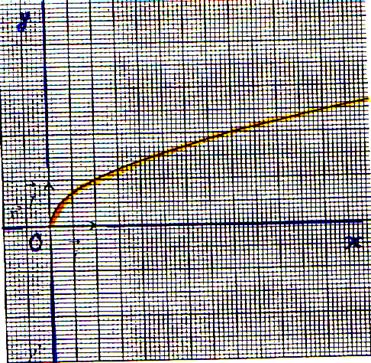
X	Fonction racine carrée
X	Fonction homographique

ETUDE TYPE D’ UNE FONCTION :

Etudier une fonction c’est :

A partir de f : R R

x f(x)

1°)Donner l’ensemble de définition.

2°)Faire une étude aux bornes du domaine de définition :

a) que se passe-t-il pour f (x) quand « x » tend vers -¥ ?

b) que se passe-t-il pour f (x) quand « x » tend vers +¥ ?

c) que se passe-t-il pour f (x) quand « x » = 0

d) résoudre  f (x) = o

3°)Donner le sens de variation :

il faudrait calculer le taux d’accroissement

4°) Construire le tableau de variation :

type

x	-¥ 0 +¥
f(x)	? ? ? ? ?sens donner avec des flèches

5°) Faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )

Repère cartésien

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) Nommer les étapes qui concernant l’étude d’une fonction :

EVALUATION:

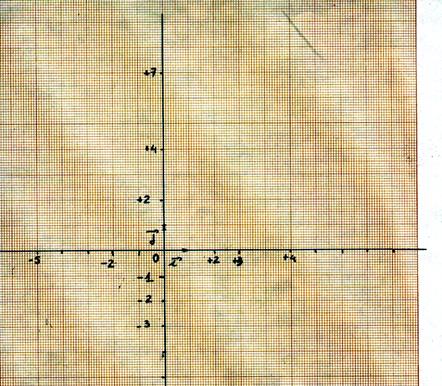
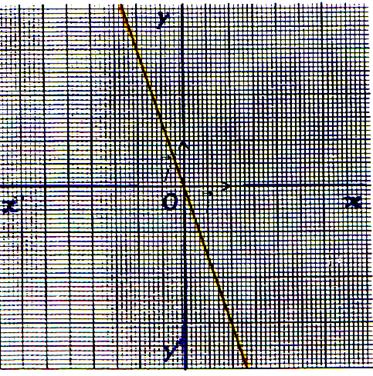
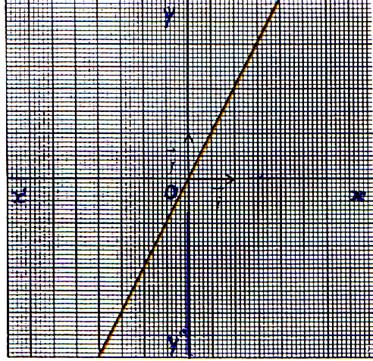
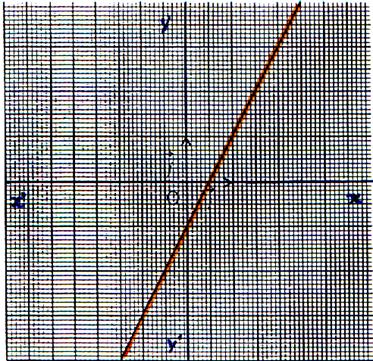
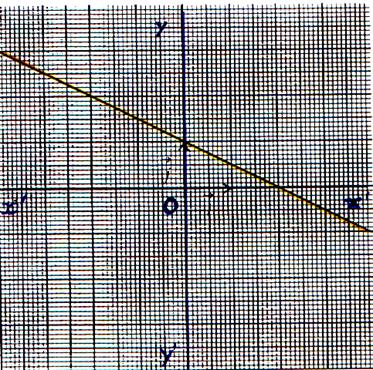
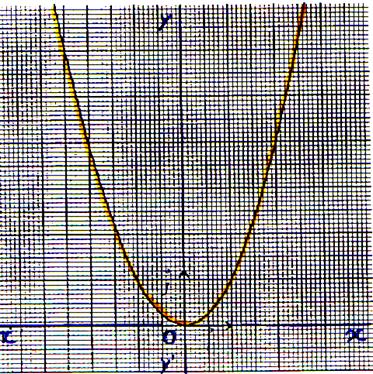
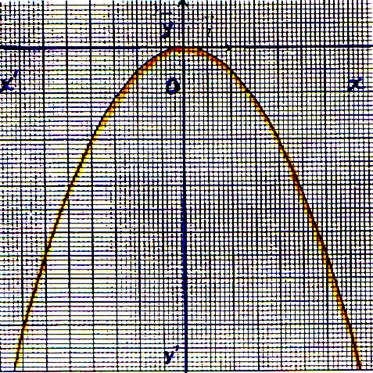
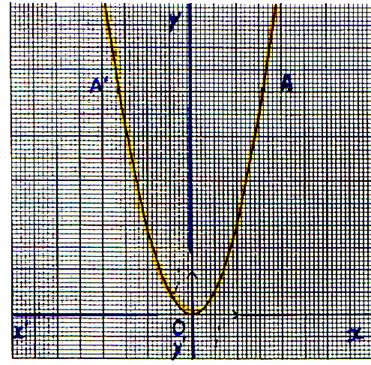
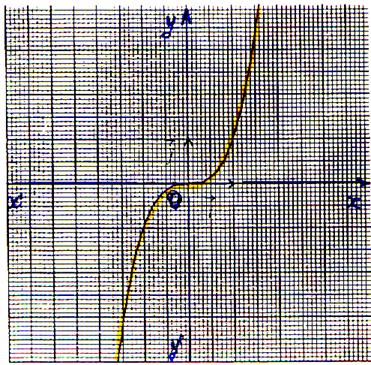
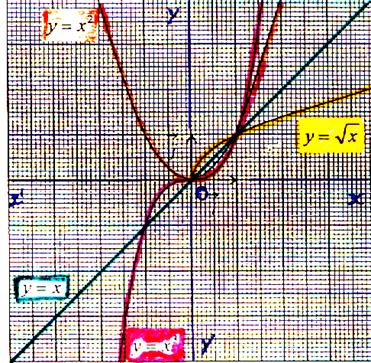
Commentez les représentations graphiques suivantes :

( forme de l’équation,Ensemble de définition,particularité : (est-elle paire ou impaire ? ) Etude aux bornes du domaine de définition, Sens de variation , le tableau de variation .

1°)

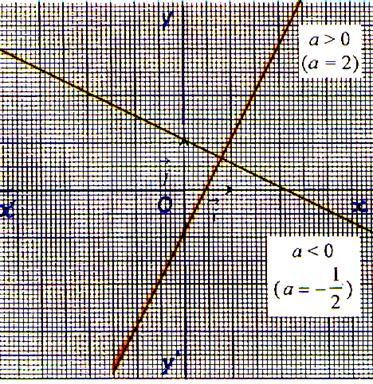
2°)

N°3

N°4
N°5

N°6
N°7

N°8
N°9

N°10

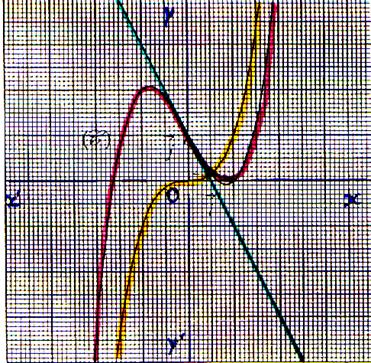
N°11 Commentez les tracés

N°12 Commentez : les tracés

CORRIGE :

Etudier une fonction c’est :

A partir de f : R R

xax

1°) donner l’ensemble de définition.

2°) faire une étude aux b o r n es du domaine de définition :

a) que se passe-t-il pour f (x) quand « x » tend vers -¥ ?

b) que se passe-t-il pour f (x) quand « x » tend vers +¥ ?c) que se passe-t-il pour f (x) quand « x » = 0

d) résoudre  f (x) = o

3°)donner le sens de variation : calculer le taux d’accroissement

4°) construire le tableau de variation :

type

x	-¥ 0 +¥
f(x)	? ? ? ? ?sens donner avec des flèches

5°) faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )