DOSSIER :La fonction affine (cours n°2)

Pré requis:

La fonction affine (niveau V)
Les Fonctions numériques

ENVIRONNEMENT du dossier:

Index

Objectif précédent : 1°)L’étude d’une fonction (info).

Objectif suivant : 1°) Les fonctions usuelles 2°)la représentation graphique

1°) tableau 2°) La fonction affine(généralités)

Leçon : ETUDE DE LA FONCTION AFFINE

FONCTION AFFINE : f : x a x+ b

INFORMATIONS

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS :

 Exemple 1 : on propose d’étudier la fonction f : R R

X 2 x - 1

ETUDE 1 de f(x) = 2x -1

1°) Ensemble de définition. Df = R

2°) Etude aux bornes du domaine de définition Df:

a) que se passe-t-il pour f (x) quand « x » tend vers -¥ ?

f (x) tend vers -¥ quand « x » tend vers -¥

b) que se passe-t-il pour f (x) quand « x » tend vers +¥ ?

f (x) tend vers +¥ quand « x » tend vers +¥

c) que se passe-t-il pour f (x) quand « x » = 0 f (o) = 1

d) résoudre  f (x) = o 0 = 2 x-1 donc x =

3°)Sens de variation :

calculer le taux d’accroissement : pas nécessaire le taux correspond à « a »

le coefficient de « x » est négatif ( a = 2 ) , f est donc strictement décroissante sur Df

4°) le tableau de variation :

x	-¥ 0 +¥
f(x)	+¥ -1 -¥

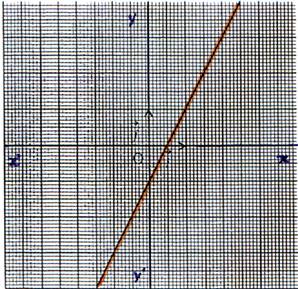
5°) Représentation graphique

La représentation graphique de la fonction f est une droite d’équation y = 2x-1 passant par l’origine du repère et le point de coordonnées (0 ; -1 ) et le point de coordonnées ( ; 0 ) ; ( 1 ; 1)

ETUDE Exemple 2 on se propose d’étudier f : R R

x- x +1

ETUDE 2 :

1°)Ensemble de définition. Df = R

2°)Etude aux bornes du domaine de définition Df:

b) que se passe-t-il pour f (x) quand « x » tend vers -¥ ?

f (x) tend vers +¥ quand « x » tend vers -¥

b) que se passe-t-il pour f (x) quand « x » tend vers +¥ ?

f (x) tend vers -¥ quand « x » tend vers +¥

c) que se passe-t-il pour f (x) quand « x » = 0

f (o) = 1

d) résoudre  f (x) = o 0 = - x +1 donc x = 2

3°)Sens de variation :

On peut calculer le taux d’accroissement : cela n’est pas nécessaire ; le taux correspond à « a »

le coefficient de « x » est négatif ( a = - ) , f est donc strictement décroissante sur Df

4°) le tableau de variation :

x	-¥ 0 +¥
f(x)	+¥ 1 -¥

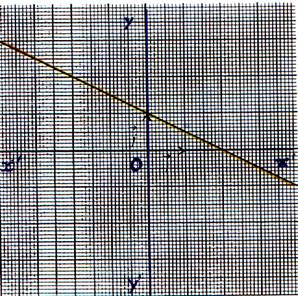
5°) Représentation graphique :

La représentation graphique de la fonction f est une droite d’équation y = -x +1 passant par le point de coordonnées (0 ; 1 ) ; (1 ; ) , (0 ;2)

Des exemples précédents : On retiendra le cas général  suivant :

FONCTION AFFINE : f : xa x + b

INFORMATIONS

f : R R

xa x + b

1°) Ensemble de définition. Df = R

2°) Etude aux bornes du domaine de définition Df:

a < 0	a > 0
f (x) tend vers +¥ quand « x » tend vers -¥ f (x) tend vers -¥ quand « x » tend vers +¥ f (o) = b	f (x) tend vers +¥ quand « x » tend vers +¥ f (x) tend vers -¥ quand « x » tend vers -¥ f (o) = b

3°)Sens de variation :

a < 0	a > 0
f est donc strictement décroissante sur Df	f est donc strictement croissante sur Df

4°) le tableau de variation :

a < 0		a > 0
x	-¥ 0 +¥	x	-¥ 0 +¥
f(x)	+¥ b -¥	f(x)	+¥ b -¥

°) Représentation graphique :

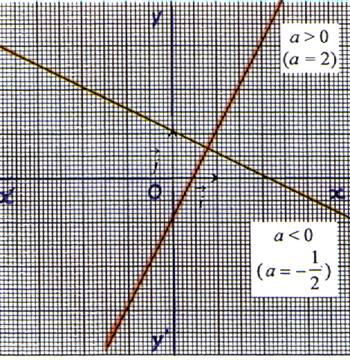
La représentation graphique de la fonction f est une droite d’équation y = ax + b passant par les points de coordonnées : ( 0 ; b ) ; (1 ; a + b ) et (-  ; 0 ) commentaires : deux cas : la droite est dite « croissante » ou « décroissante » . la droite ( D2) « orange » est croissante. La droite ( D1) « jaune » est décroissante.

CONTROLE:

1°) Donner les étapes concernant l’étude d’une fonction de la forme  : ax +b

2°) Etude générale de la fonction de la forme : « a x + b »

a) Donner l’ensemble de définition.

b) Faire une étude aux bornes du domaine de définition :

c) Donner le sens de variation :

d ) Construire le tableau de variation : (vous aider du tableau suivant)

x	-¥ 0 +¥
f(x)

e ) faire la représentation graphique : utiliser le repère cartésien . le plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )

EVALUATION:

1° ) Etudier la fonction : f : R R

x 2 x – 1

2 °) Etudier la fonction : f : R R

x - x +1