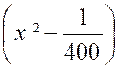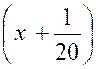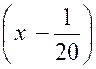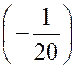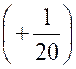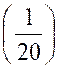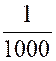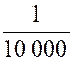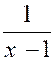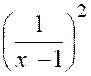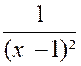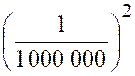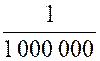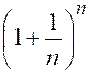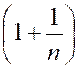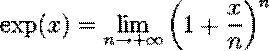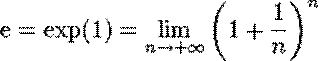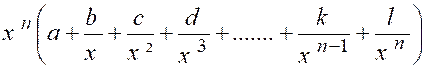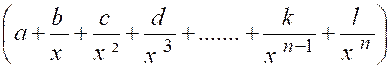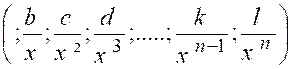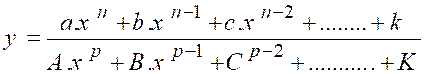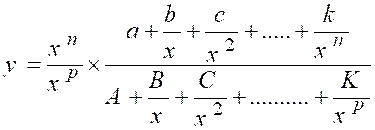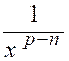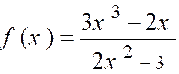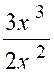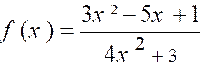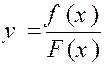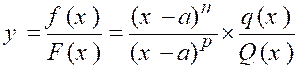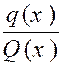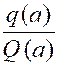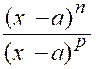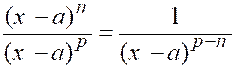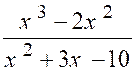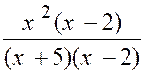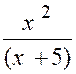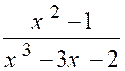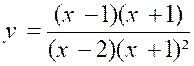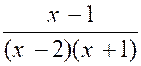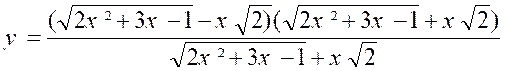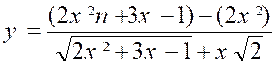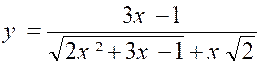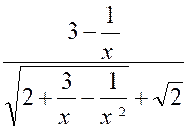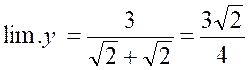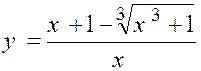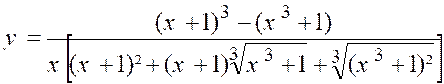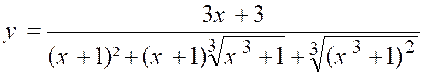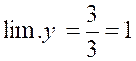Pré requis
|
|
ENVIRONNEMENT du
dossier :
|
Objectif
précédent : |
Objectif suivant : |
|
||
|
INFORMATIONS : Module ( niveau
3 et 2 ): calcul algébrique |
||||
LES
CALCULS FRACTIONNAIRES :
Suite : NOTIONS SUR LES LIMITES ( cours n°1 )
|
Chapitres |
|
|
|
|
|
|
|
|
1.
Définitions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.
Limite d’une fraction rationnelle dont les deux termes tendent
simultanément vers « zéro » |
|
|
|
|
|
|
|
|
Travaux
auto formatifs. |
|
|
Corrigé |
||
|
TEST |
COURS
|
|
|||||
|
|
Cours en lien avec les études de
fonctions…………. |
|
|
|
|
|
|
|
Soit
« y » une quantité variable, fonction d’une autre quantité variable
attribuée à « x ».On dit que « y » a pour limite
« b » quand « x » tend vers « a » ,si,
lorsqu’on donne à « x » des valeurs suffisamment voisines de la
valeur « a » , les valeurs correspondantes de « y » différent d’aussi peu qu’on le veut de la
valeur de « b ». La quantité
« y » tend vers la limite « b » par valeurs supérieures
ou par valeurs inférieures , suivant que la
différence « y – b » reste positive ou négative.(voir la suite pour les deux exemples) |
|
|
|
On dit
qu’une quantité « devient infinie » si elle parvient à dépasser en
valeur absolue tout nombre arithmétique si grand qu’on puisse le concevoir. |
|
|
|
Une
quantité algébrique peut devenir infini de deux
façons : Soit en
étant positive, soit en étant négative. Dans le
premier cas, on dit quelle « croît
indéfiniment » par valeurs
positives, ou encore qu’elle tend vers « + Dans le
second cas , |
|
|
|
Remarque :
Lorsqu’une quantité devient infinie par valeurs positives ou négatives , on dit souvent qu’elle croît
« indéfiniment ». Attention : Cette façon de parler , consacrée par
l’usage, est évidemment incorrecte lorsque la quantité est négative , puisqu’alors elle décroît quand
elle tend vers « - L’expression « croître indéfiniment »
se rapporte donc, en somme, à la valeur absolue de la quantité qui devient
infinie. |
|
|
|
Exemples : |
|
|
|
Exemple N°1 :
La fonction « y =
4 x² + 3 » a pour
limite « 3 » quand on
fait tendre « x » vers « 0 » Remarquons
d’abord que la différence « y – 3
= 4 x² » étant toujours positive quand « y » tendra vers sa
limite « 3 » par valeurs supérieures ?. Il faut
prouver qu’on peut prendre « x » assez voisin de « 0 »
pour que la différence « y – 3 » soit aussi petite que l’on veut , par exemple : < Or, il
suffit, pour cela, que « x » vérifie l’inégalité « 4 x² < |
|
|
Ou : 4 |
|
|
|
|
On
donnera à « x » une valeur
comprise entre |
|
|
|
On
pourrait de même rendre « y – 3 » plus petit que |
|
|
|
|
|
|
|
Exemple N°1 : La fonction « y =
Quelque soit le signe de
« y », son carré devra être supérieur à ( 1 000 000)² : D’où l’on déduit D’où l’on déduit : ( x – 1 ) ² - Et par suite : « 1
- Il suffit donc que la valeur de « x » choisie diffère de
« 1 » , en plus ou en moins de moins
de « Si « x » est « > 1 » ,
« y » est positif ; donc ,
« x » tendant vers « 1 » par valeurs supérieures,
« y » croît indéfiniment par valeurs positives. Si « x » est « <
1 » , « y » est négatif ; par
suite , « x » tendant vers
« 1 » par valeurs inférieures, « y » décroît indéfiniment
par valeurs négatives . |
|
|
|
2°) Limites d’une somme de fonction : d’un
produit ; d’un quotient ; d’une puissance ;d’une
racine ; ( Théorèmes) |
|
|
|
Théorème
1 : La limite d’une somme algébrique de
fonction est égale à la somme algébrique de leurs limites. |
|
|
|
Soient , par exemple, « u » , « v » ,
« w » trois fonctions d’une même variable indépendante
« x ». Si ,
lorsque « x » tend vers « a » , les fonctions « u » , « v » ,
« w » ont respectivement pour limites « A » ,
« B » , « C », la somme algébrique
« u + v - w »aura pour limite « A +
B - C » . En effet , soit
« Donnons à
« x » une valeur « a + h », très voisine de
« a » ( « h »
étant positif ou négatif, mais très petit en valeur absolue) . Les
fonctions « u » ,
« v » , « w » ont ayant pour limites « A » ,
« B » , « C » , prendront pour « x = a +
h » des valeurs : « A + « On a
alors pour « x = a + h » :
« u + v - w = A + B – C + ( Or , rien ne limite la petitesse des valeurs absolues
des nombres « Alors la
valeur absolue ( Il est
clair , en effet , que ( Par suite , d’après la relation ( 1 )
, « u + v - w » différera de
« A + B – C » de moins de « |
|
|
|
Théorème
2 : La limite d’un produit de fonctions est
égale au produit de leurs limites. |
|
|
|
Soient
d’abord deux fonctions « u » et
« v » d’une même variable indépendante « x ». Si , lorsque « x » tend vers
« a », les fonctions « u » et « v »ont respectivement pour limite « A »
et « B » , le produit « u . v » aura pour limite «
A .B » Soit , en effet ,
« |
|
|
|
Donnons à
« x » une valeur « a + h » ,
« h » étant positif ou négatif , mais très petit en valeur absolue.
Les fonctions « u » et « v » prennent alors les valeurs
«A+ On a ainsi , pour « x = a + h » |
|
|
|
« u . v = ( A+ |
|
|
|
Pour une
valeur de « h » suffisamment petite ,
« Alors la
valeur absolue de « B ; et d’
après la relation ( 1) , « u . v »
diffèrera de « A.B » de
moins de « Soient
maintenant trois fonctions « u » ,
« v » , « w » ayant
respectivement pour limites « A » , « B » ,
« C », le produit « u v w » peut être considéré comme le produit
des deux facteurs : « u.v » et
« w ». D’après
ce qui précède, « u.v » a pour limite
« A.B »et « w » a pour limite « C », donc
« u.v.w »a pour limite
« ABC ». |
|
|
|
|
|
|
|
Théorème
3 : La limite d’un quotient de fonctions est égale au quotient de leurs
limites. |
|
|
|
Soient
d’abord deux fonctions « u » et
« v » d’une même variable indépendante
« x ». qui lorsque
« x » tend vers « a » ont respectivement pour « A » et « B » ;
« B » n’étant pas nul. Le
quotient « En effet , posons « Nous
aurons alors « u = v w » Et comme
la limite d’un produit « vw » est le
produit des limites « BC » de ses facteurs ,
on a « A = BC » et par suite
« C = |
|
|
|
Remarque . L’exposé de ce
théorème n’est pas rigoureux .Il faudrait d’abord démontrer l’existence de la
limite « C » de « w » par un raisonnement analogue à
celui du théorème 2. Mais une
telle rigueur n’est pas indispensable dans ce cours aussi élémentaire. La même
remarque s’applique au théorème 5 , ci-dessous. |
|
|
|
|
|
|
|
Théorème
4 : La limite de la puissance « nième » d’une
fonction est égale à la puissance
« nième » de sa limite. |
|
|
|
C’est une
conséquence du théorème 2 . Si la fonction
« u » a pour limite « A » , « u n »
, qui est un produit de « n » facteurs égaux à « u » , a
pour limite « A n » |
|
|
|
|
|
|
|
Théorème
5 : La limite de la racine « nième » d’une fonction
est égale à la racine « nième » de sa limite. |
|
|
|
Soit à
chercher la limite de « Nous aurons en élevant à la puissance
« n » :
« u = v n » Mais
comme la limite d’une puissance « v n » est la puissance
« nième » de la limite de « v » . « A = B n »
d’où l’on conclut :
B = |
|
|
|
Remarque sur l’application des théorèmes
précédents. |
|
|
|
Les
théorèmes sur la limite d’une somme ou celle d’un produit ne sont vrais , en général, que si le nombre des termes de la
somme ou des facteurs du produit est
« limité ». Il faut
se garder de les appliquer à des sommes algébriques d’une infinité de termes «( séries) ou à des produits d’un nombre infini de
facteurs. |
|
|
|
Exemple . (prépare à l’étude de la fonction exponentielle) Le
produit |
|
|
|
Info : Fonction
exponentielle réelle
Définitions
Il
existe plusieurs points d'entrée possible pour la définition de la fonction
exponentielle : par la propriété de sa dérivée (dérivée égale à la
fonction), par ses propriétés algébriques (transforme une somme en produit),
ou par son développement en série. Par
une équation différentielle
Définition — On appelle
fonction exponentielle l'unique fonction dérivable vérifiant l'équation
différentielle et la condition initiale suivante :
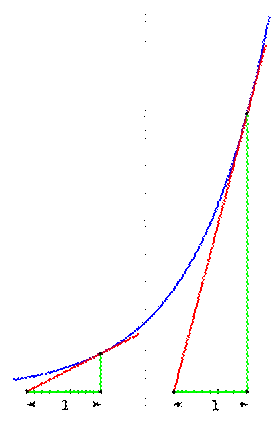
Courbe
d'équation « y=exp. (« x ») »
et quelques sous-tangentes Si
on note « exp. » cette fonction, le
processus de construction conduit à définir « exp.( x ) » par
Le
nombre « e » égal à exp. (1) est alors défini par
Cette
propriété d'être sa propre dérivée se traduit par une propriété sur la
sous-tangente à la courbe représentative de exp. La sous-tangente,
c'est-à-dire la distance qui sépare le réel x
de l'abscisse du point d'intersection de la tangente à la courbe au point
d'abscisse x avec l'axe des x est constante et vaut 1. |
|
|
|
|
|
|
|
|
|
|
Info +++ |
3°)
Valeurs remarquables d’une
fraction . ( info +++ : Cours N°2 sur
« les limites ») |
|
|
|
Nous ne ferons qu’énoncer les propriétés
suivantes, qui sont des conséquences immédiates des théorèmes précédents. |
|
|
|
1°) Si un des facteurs d’un produit croît
indéfiniment, et aucun autre ne
tendant vers « 0 », le produit va croître indéfiniment. |
|
|
|
2°) Si le numérateur d’une fraction ayant une
limite différente de « 0 », le dénominateur tend vers
« 0 », la fraction croît indéfiniment. |
|
|
|
3°) Si le numérateur d’une fraction restant fini,
le dénominateur croît indéfiniment, la fraction tend vers « 0 ». |
|
|
|
En résumé, les
formes suivantes que l’on rencontre souvent en cherchant la limite d’un
produit ou d’une fraction : sont : « A x 0 » ;
« A x « A »
étant une quantité finie et non nulle, ont des valeurs bien déterminées qui
sont : « A x 0 =
0 » ; « A
x |
|
|
|
Si l’un des facteurs d’un produit croît
indéfiniment tandis que l’autre tend vers « 0 », ou si les deux
termes d’une fraction tendent simultanément vers « 0 », on ne peut
rien affirmer. Le produit ou la fraction peuvent
, suivant les cas, tendre vers « 0 », avoir une limite finie
« A », ou croître indéfiniment. Il en est de même d’une fraction dont les deux
termes croissent indéfiniment, ou d’une différence dont les deux paries
croissent indéfiniment avec le même signe. |
|
|
|
Ainsi les formes : « (voir plus loin
comment on va lever « l’indétermination » ; on dit
aussi : comment on calcule la vraie valeur de ces expressions…….. . |
|
|
|
|
|
|
|
|
|
|
|
4°)
Valeur d’un polynôme en
« x », pour une valeur de
« x » infinie. |
|
|
|
Un polynôme entier en « x » , de degré quelconque , croît indéfiniment avec
« x » et , pour des valeurs de « x » suffisamment grandes
en valeur absolue, il prend le signe de son terme de degré le plus élevé. |
|
|
|
Soit , en effet , le polynôme de degré « n ». « y = a x n + b x n-1 + c x n-2 + ….+ k x + l » |
|
|
|
Quand
« x » croît indéfiniment, les différents termes du polynôme, sauf
le dernier , croissent indéfiniment , mais sans
avoir nécessairement le même signe ; on peut affirmer que
« y » augmente indéfiniment. |
|
|
|
Exemple : prenons le
polynôme : « 5 x² - 3 x + 2 » Quand « x » tend vers l’infini positif , le
polynôme se présente sous la forme indéterminée : «
Mettons « x n » en facteur , nous aurons identiquement : « y = « y » est maintenant un produit de deux
facteurs , dont le premier « x n »
croît indéfiniment avec « x ». Dans le second facteur Donc « y » ,
produit de deux facteurs dont le premier croît indéfiniment et dont le second
a pour limite « a » ( quantité non nulle) croît indéfiniment. De plus, comme la parenthèse a pour limite
« a » , on peut prendre « x »
assez grand en valeur absolue pour que cette parenthèse diffère d’aussi peu
qu’on veut de sa limite. Pour ces valeurs de « x » , elle prend le signe
de « a » et « y » prend le signe de son terme de
plus haut degré « a x n » . Nous retrouvons ainsi le
résultat (à revoir dans : « le signe d’un polynôme de degré quelconque » |
|
|
|
|
|
|
|
Notation. |
|
|
|
Lorsqu ’ on représente le polynôme par la notation abrégée : « f ( x ) » on désigne par « f ( + |
|
|
|
Exemples |
|
|
|
N°1 : quand « x » croît indéfiniment
, le polynôme : « f ( x
) = x 4 – 3 x » croît
indéfiniment par valeurs positives , car son terme de plus haut degré « x 4 » est positif,
quel que soit le signe de « x ». En effet, les puissances paires
d’un nombre positif ou négatif sont toujours positives. On a donc :
« f ( + |
|
|
|
N°2 : Dans les mêmes conditions que
ci-dessus ; le polynôme : « f ( x ) = x 3 – 3 x² + 1 » croît indéfiniment par valeurs positives
, ou négatives en même temps que « x » ; En effet , son
premier terme « x 3 »
est positif ou négatif avec « x », car les puissances impaires d’un
nombre négatif sont négatives. On a donc ,pour ce
polynôme : « f ( + |
|
|
|
|
|
|
|
Valeur d’une fraction rationnelle lorsque
« x » tend vers l’ infini |
|
|
|
Soit une fraction « y » dont les deux
termes sont des polynômes en « x » de degrés quelconques en « n » et « p ». « |
|
|
|
Quand « x » augmente indéfiniment, les
polynômes du numérateur et du dénominateur augmentent indéfiniment. ( voir chapitre précédent ) , la fraction prend la forme
indéterminée : « Décomposons les deux termes en produits, en
mettant en facteur dans chacun d’eux la plus haute puissance de
« x ». Nous aurons : « Quand « x » croît indéfiniment, toutes
les fractions qui ont « x » , ou une
puissance de « x » au
dénominateur tendent vers « 0 » (voir valeur
remarquable d’une fraction ci-dessus) et le second facteur tend vers la limite
« |
|
|
|
Si
« n » est égal à « p » : le premier facteur « |
|
|
|
Si
« n » est plus petit que « p » : le premier
facteur « |
|
|
|
Si
« n » est plus grand que
« p » :
le premier facteur
« Ainsi une fraction rationnelle de « x »
croît indéfiniment en même temps que « x » ,
si son numérateur est de degré supérieur à celui de son dénominateur ;
elle tend vers « 0 » si son numérateur est de degré inférieur à
celui de son dénominateur ; enfin , elle a une limite finie et non nulle
si ses deux termes sont de même degré ; cette limite est alors le
quotient des coefficients des termes de plus haut degré au numérateur et au
dénominateur, |
|
|
|
Exemples : |
|
|
|
N°1 : Soit la
fraction : Elle croît indéfiniment avec « x » et
prend le signe du quotient : |
|
|
|
N°2 :
Soit la fraction : Lorsque « x » croît indéfiniment
, la fonction a pour limite : « « f ( + |
|
|
|
Limite
d’une fraction rationnelle dont
les deux termes tendent simultanément vers « zéro » |
|
|
|
Soit une fraction : |
|
|
|
Supposons que pour « « f ( a ) = 0 » et
« F ( a )) = 0 » |
|
|
|
Proposons
nous de trouver la valeur limite de cette fraction
quand « x » tend vers « a ». Les polynômes « f ( x
") » et « F ( x
) » s’annulant pour « x = a » sont divisibles par « x – a » . Divisons – les par « x – a » , ainsi que les quotients successifs que nous
trouverons, autant de fois qu’il sera possible . Nous pourrons mettre les deux polynômes sous la
forme : f ( x ") = ( x – a) n
. q ( x) »
et « F ( x ) = ( x – a) p . Q ( x)» ; les derniers quotients obtenus « q ( x) » et «Q (
x) » ne s’annulant plus pour « x = a » La fraction donnée ,s’écrira :
Quand « x » tend vers « a »,
le second facteur « Si « n » est égal à « p » le premier facteur « |
|
|
|
Si « n » est plus grand que « p » le premier facteur « Enfin, si « n » est plus petit
« p », le premier facteur : « |
|
|
|
Exemple : |
|
|
|
La fraction : « y = |
|
|
|
En divisant les deux termes de la fraction par
« x – 2 » , on trouve : « et la limite de « y »
, pour « x = 2 » est
« |
|
|
|
N°2 : Trouver la limite de la fraction « |
|
|
|
Les deux autres termes s’annulant pour « x –
1 » sont divisibles par « x +1 » ; de plus, le quotient
du dénominateur par « x +
1 » , « x² - x -2 » s’annulant encore pour « x = -1 » est
divisible par « x + 1 » , et l’on a : « Quand « x » tend vers « -1 »,
le dénominateur tend vers « 0 » et la fonction « y »
augmente indéfiniment. : ( forme « |
|
|
|
|
|
|
|
|
|
|
|
N°1 : Quelle est la limite de « y = Si « x » augmente indéfiniment par
« valeurs négatives » , le polynôme de
degré pair « 2x² + 3 x -1 »
tend vers « + Si « x » augmente indéfiniment par
« valeurs positives » la fonction « y » se présente sous
la forme « « Cherchons à ramener l’expression à la
forme : « Nous aurons : « et , en observant que le numérateur, produit d’une différence par une somme,est une différence de carrés. « « Quand « x » tend vers « + Divisons les deux termes par
« x » ; il vient : « Car il faut diviser le dénominateur par « x= Or , « x » augmentant indéfiniment , il reste :
(cette notation veut dire : limite de
« y » égale……) |
|
|
|
N°2 : Quelle est la limite de « |
|
|
|
Les deux termes s’annulent pour « x =
0 » et le rapport prend la forme « « u² - v² = ( u – v) ( u² + u.v + v²) Posons
« x + 1 = u » ;
« Nous aurons :
Développant le numérateur et supprimant le
facteur « x » commun aux deux termes, il vient :
|
|
|
|
Résumé : |
|
|
|
On dit , qu’une fonction »y » d’une
variable « x » tend vers une limite « b » lorsque
« x » tend vers « a », si , lorsque « x » se
rapproche de plus en plus de la valeur « a », les valeurs de
« y » diffèrent de moins en moins de « b ». La limite d’une somme de fonctions est égale à la somme de leurs
limites. De même , pour un produit , un quotient , une
puissance , une racine. Pour « x » infini, un polynôme se comporte comme son terme
de plus haut degré et de même , une fraction rationnelle se
comporte comme le rapport des termes de degré les plus élevés. Pour trouver la limite d’une fraction rationnelle dont les deux termes
tendent simultanément vers zéro, on divise ces deux termes par le facteur
commun qui les annulait à la fois. |
|
|
|
|
|
|
|
|
|