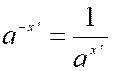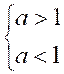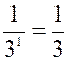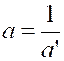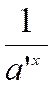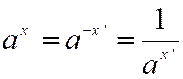Pré requis:
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant : |
|
|
|
|
|||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
DOSSIER
: NOTIONS sur LA FONCTION EXPONENTIELLE
|
|
|||||||
|
|
Voir le système de logarithmes
népériens. |
||||||
|
|
|||||||
|
|
|||||||
|
|
|
||||||
|
|
|
||||||
|
|
|
Travaux
auto formatifs |
|
|
Corrigé
des Travaux auto formatifs |
||
|
TEST |
Interdisciplinarité : |
|
|||||
|
|
Corriger des travaux. |
|
|
|
|
|
|
|
Définition : |
|
|||||||||||||
|
|
Si on élève un nombre fixe positif « a » à une puissance variable
« x » , la fonction correspondante
« a x » est appelée « la fonction
exponentielle ». Il importe de définir « a x »,
c'est-à-dire la signification de cette notation suivant les différentes
valeurs de « x ». 1°) « x » étant entier et positif , « a x » représente le
produit de « x » facteurs égaux à « a ». 2°) « x » étant fractionnaire et
positif, de la forme |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
3°) « x » étant incommensurable et positif , « |
|
||||||||||||
|
|
4°) « x » étant négatif ; mettons
l’hypothèse en évidence en posant
« x = - x’ » , « x’ »
étant essentiellement positif. on a vu que
|
|
||||||||||||
|
|
5°) Remarque « a0 = 1 » par convention justifiée . |
|
||||||||||||
|
|
On appelle donc , une
fonction exponentielle , une fonction de la
forme : y
= a x |
|
||||||||||||
|
|
Dans laquelle « a » est un nombre positif fixe et « x » une variable pouvant prendre des valeurs ( négative , nulle ou positive ) ; de
- |
|||||||||||||
|
|
C’est la première fois que nous rencontrons ainsi
la variable « x » en exposant. |
|||||||||||||
|
|
|
|||||||||||||
|
|
Etude
de y = a x : 2 cas |
|||||||||||||
|
|
|
|||||||||||||
|
|
C’est l’étude des logarithmes qui conduit à la
considération de cette fonction que nous examinons ; nous supposons que
« x » peut prendre des valeurs positives ou négatives très voisines les unes des autres mais
toujours commensurables. |
|||||||||||||
|
|
|
|||||||||||||
|
|
Calculs : soit l’équation y = 3 x ; on donne les valeurs de
« x » ; 1°) Remplir
le tableau ; calculer les valeurs
de « y » |
|||||||||||||
|
|
|
|||||||||||||
|
« x » |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
9 |
|
|||||
|
« y » |
3 -1 = |
3 0 = 1 |
31= 3 |
32= 9 |
33= 27 |
34= 81 |
35= 243 |
39=19 683 |
|
|||||
|
|
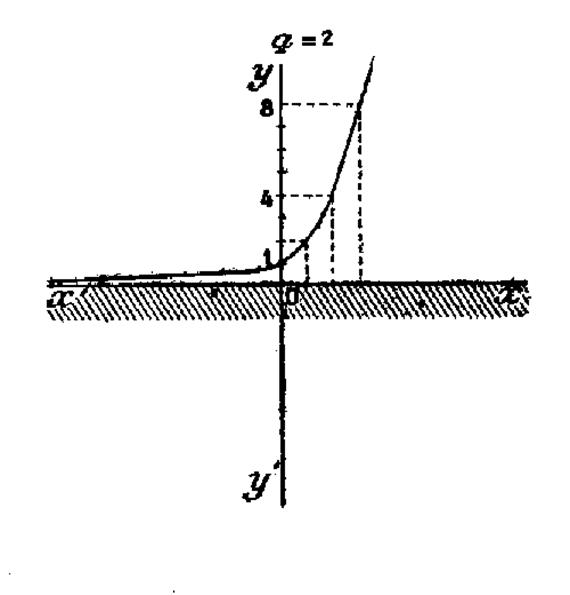
2°) consigne : Faire la représentation graphique
dans un repère orthonormé… |
|
||||||||||||
|
Variations de la fonction exponentielle. |
|
|||||||||||||
|
|
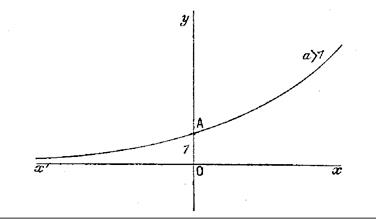
1°) Cas
« a » > 1 ;
( Remarque « a0 = 1 » par convention justifiée .) |
|
||||||||||||
|
|
La fonction y = a x est continue est croissante , en effet la
variable « x » ayant une
valeur x1 donnons lui un accroissement positif
« h », et examinons l’accroissement ( a x1 étant fixe
et ( ah - 1)
étant aussi petit que l’on veut , il est en outre positif, les deux
facteurs sont positifs . Quand « x » varie de - |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Forme générale : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
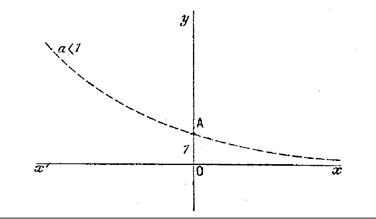
1°) Cas
« a » < 1 ; ( a
> 0) ; Remarque « a0 = 1 » par convention justifiée . |
|
||||||||||||
|
|
La fonction y = a x est continue est croissante
, en effet posons D’après ce qui a été vu précédemment a ‘x varie de 0 à + Nous allons d’abord, pour plus de simplification , faire varier « x » de « 0 » à
« + Remarque « a0 = 1 » par convention justifiée ., lorsque « x » augmente , comme
« a<1 », d’après les théorèmes précédemment démontrés , « a
x » va en décroissant,
que « x » croisse par valeurs entières ou fractionnaires ou
incommensurables , et lorsque « x » croît indéfiniment sans
limite, « a x » se rapproche de plus en plus de 0 qui est
sa limite. Donc , « a<1 » , « a x » décroît
constamment de « 1 »
à « 0 » , quand « x » croît constamment de
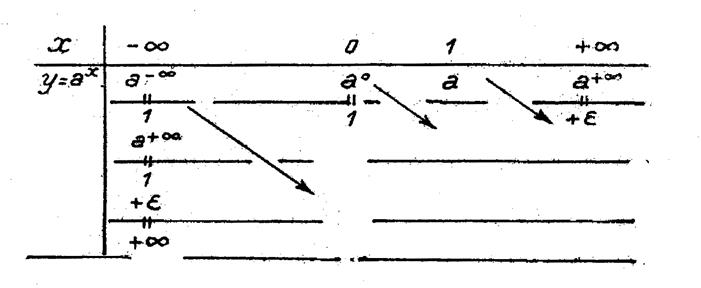
« 0 » à « + Faisons varier maintenant « x » de -
Quand
« x » varie de - Donc On peut résumer ce qui pré cède dans les tableaux suivants. |
|
||||||||||||
|
|
a > 1 |
|
a < 1 |
|
||||||||||
|
« x » |
« a x » |
|
« a x » |
|||||||||||
|
- |
|
|
- |
|
||||||||||
|
croît |
croît |
|
croît |
décroît |
||||||||||
|
0 |
1 |
|
0 |
1 |
||||||||||
|
croît |
croît |
|
croît |
décroît |
||||||||||
|
+ |
+ |
|
+ |
0 |
||||||||||
|
|
Aussi : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Forme générale : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Remarque : Il est évident que si « a =
1 » ;la fonction est constante et elle ne présente pas d’intérêt. |
|
||||||||||||
|
|
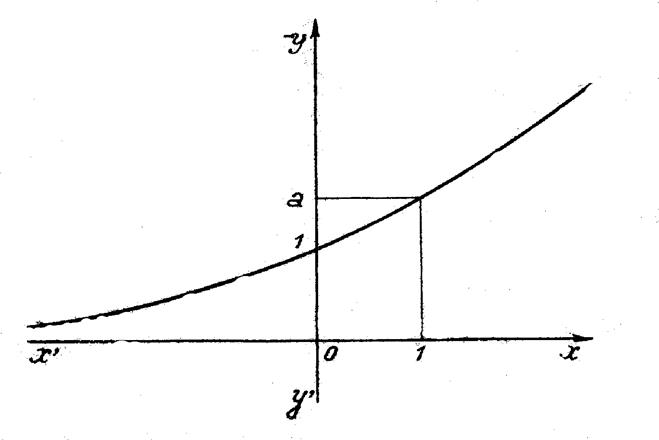
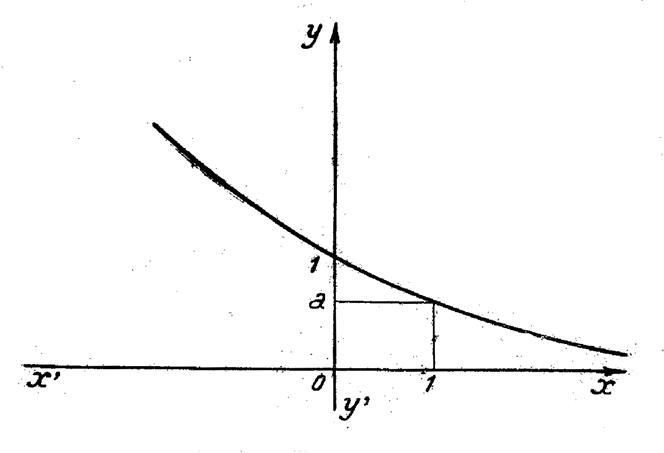
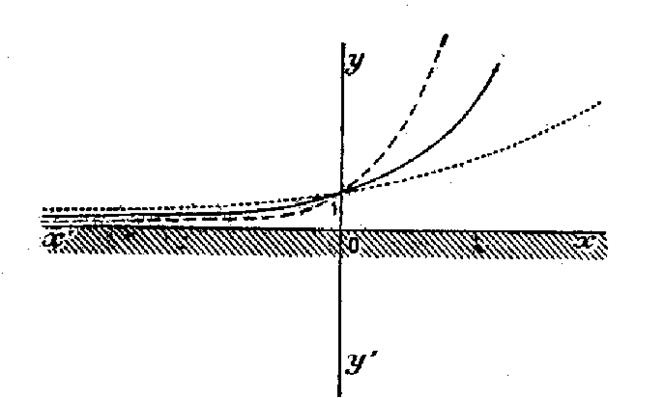
Les considérations précédentes permettent de
tracer les courbes figurées ci-dessous : L’une d’elles en trait plein correspond au cas de « a>1 » , l’autre en
traits pointillés au cas « a
< 1 » . |
|
||||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
Quand on connaît la valeur numérique de
« a » on peut avoir des points de repère. |
|
||||||||||||
|
|
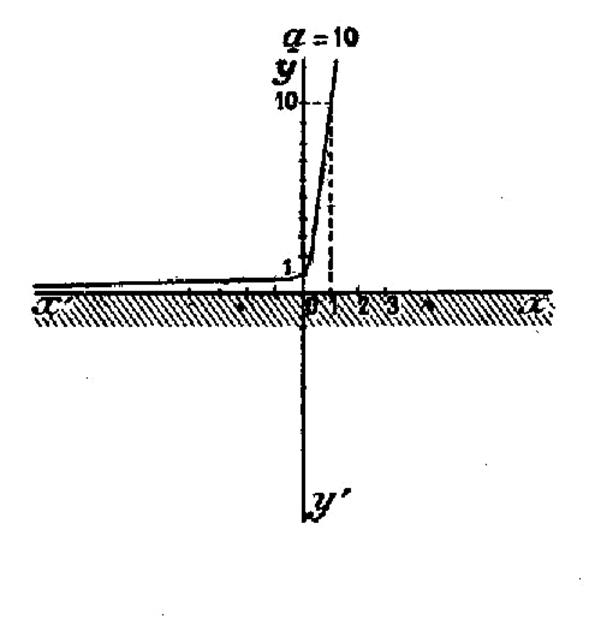
Exemple 1 : a = 10 Pour x = 1 , 10 x
= 10 ; Pour x = 2 , 10 2
= 100 ; Pour x = 3 , 10 3 = 1 000 ;….. |
Exemple 2 : a = 2 Pour x = 1 , 2 1
= 2 ; Pour x = 2 , 2 2 = 4 ; Pour x = 3 , 2 3 = 8 ; ………….. |
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
La courbe s’élève moins rapidement
. On se rend compte que « a » étant plus grand que 1 , plus la valeur numérique de « a » augmente ,
plus la courbe s’élève rapidement. |
|
||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
||
|
TRAVAUX AUTO FORMATIFS. |
|
||
|
|
|
|
|
|
|
CONTROLE : |
|
|
|
|
|
|
|
|
|
Voir le résumé ci-dessus |
|
|
|
|
|
|
|
|
|
EVALUATION : |
|
|
|
|
Exercices : Résoudre . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Domaine de définition : (Df) Df = ]
- Lim. ex = - x Lim. ex =
+
x |
|
|||
|
|
|
|
|||
|
|
On appelle donc , une fonction
exponentielle , une fonction de la
forme : y = a x |
|
|||
|
|
Dans laquelle « a » est un nombre
positif fixe et « x » une variable pouvant prendre des valeurs
de -
|
||||
|
|
C’est la première fois que nous rencontrons ainsi
la variable « x » en exposant. |
||||
|
|
C’est l’étude des logarithmes qui conduit à la
considération de cette fonction que nous examinons ; nous supposons que
« x » peut prendre des valeurs positives ou négatives très voisines les unes des autres mais
toujours commensurables |
||||
|
|
|
||||
|
|
1°)
Cas « a » >
1 |
|
|||
|
|
La fonction y = a x est continue est croissante , en effet la
variable ayant une valeur x1 donnons lui un accroissement positif
« h », et examinons l’accroissement ( |
|
|||
|
|
|
||||
|
|
|
||||
|
TRAVAUX AUTO FORMATIFS. |
|
||||
|
|
|
|
|
||
|
|
CONTROLE : |
|
|
||
|
|
|
|
|
||
|
|
Voir le résumé ci-dessus |
|
|
||
|
|
|
|
|
||
|
|
EVALUATION : |
|
|
||
|
|
Exercices : Résoudre . |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||