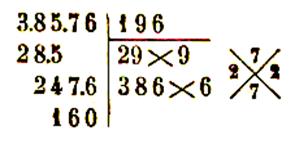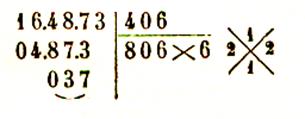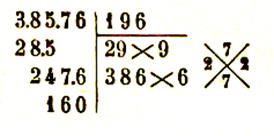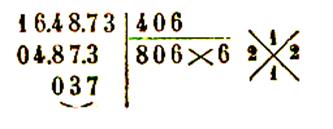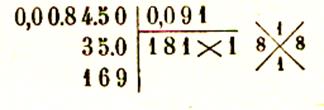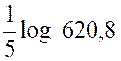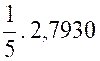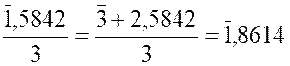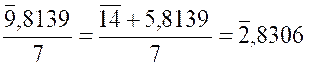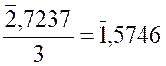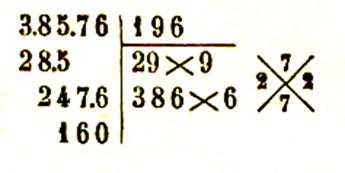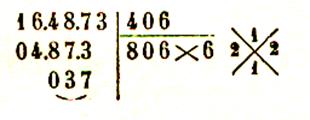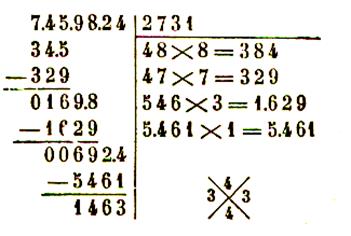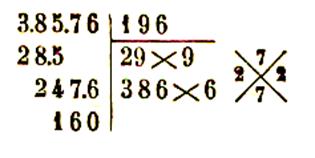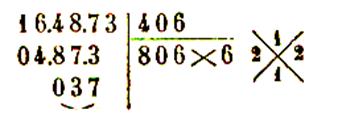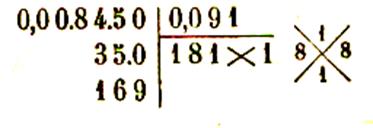|
Le
"carrée" parfait |
ENVIRONNEMENT du
dossier:
|
|
|||
|
|
|||
|
|
|||
|
|
|
|
|
DOSSIER: EXTRACTION d’ une
RACINE carrée
1)
Extraction d’une racine carrée de nombres entiers :
2)
Extraction d’une racine carrée de nombres décimaux :
et
Valeur approchée et encadrement d’une
racine carrée.
3°) Logarithmes et extraction des racines (d’indice supérieur à 2 ) .
|
COURS |
Interdisciplinarité |
|
|
Travaux
avec la calculatrice : taper des
valeurs et comparer le résultat donné
par la table numérique |
|
« extraction d’une racine carrée » Extraire la racine carrée d’un nombre
c’est trouver la racine carrée de ce nombre
1°
Extraction d’une racine carrée de nombres entiers
a)
Soit donc à trouver la racine carrée à une unité prés
du nombre 68
La connaissance des carrés des dix
premiers nombres nous indique que 68 est
compris entre les carrés parfaits 64 et
81 et que par suite sa racine carrée est
comprise entre 8 et 9 , c’est à dire que ![]() = 8 à une unité
prés ;
= 8 à une unité
prés ;
64
< 68 < 81
![]() <
< ![]() <
< ![]()
8 <
![]() < 9
< 9
b) le
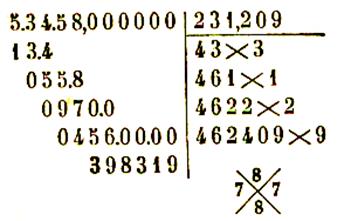
nombre est supérieur à 100 .
Règle :
pour extraire la racine carrée d’un nombre ( exemple 7
459 824 ) entier à une unité près , on le partage en tranche de deux chiffres à
partir de la droite ( 7.45.98.24 ) . Le
nombre de tranche , dont la première de gauche ( 7 )
peut n’avoir qu’un chiffre , est égal au nombre de chiffres de la racine (
4) . On dispose l’opération comme une division , les
chiffres de la racine s’inscrivant à la place du diviseur .
On extrait la racine carrée de la
première tranche à gauche ce qui donne le premier chiffre de la racine ( 2 ) . En retranchant le carré de ce chiffre ( 4 ) de la
première tranche ( 7 ) on obtient le premier reste ( 3 ) à la droite duquel on
abaisse la deuxième tranche ( 45 ) ce qui donne le premier nombre partiel ( 345
) On sépare un chiffre à droite de ce nombre ( 34.5 ) et
on divise le nombre de gauche ( 34 ) par le double de la racine ( 4 ) . Le
quotient ( 8 ) ainsi trouvé donne le deuxième chiffre
de la racine ou un chiffre trop fort . Pour l’essayer on l’écrit à droite du
double ( 4 ) de la racine déjà trouvée ( 2) et on
multiplie le nombre ( 48) ainsi formé par le chiffre ( 8 ) essayé . Si le
produit obtenu ( 384) peut se retrancher du premier nombre partiel ( 345 )
le chiffre essayé est exact , sinon ( ce qui est le cas de notre exemple ) on
essaye le chiffre (7) immédiatement inférieur et ainsi de suite jusqu’à ce que
l’on obtienne un produit ( 329 )
inférieur au premier nombre partiel ( 345 ) . On fait la différence ( 345 – 329
) ce qui donne le deuxième reste ( 16 ) à la droite duquel on abaisse la
troisième tranche ( 98 ) pour obtenir le
deuxième nombre partiel ( 1698 ) . On sépare un chiffre à la droite de ce nombre ( 169.8)
et on divise la partie de gauche ( 169 ) par le double de (54) du nombre ( 27)
déjà obtenu à la racine . Le quotient ( 3 ) est
égal ou supérieur au troisième chiffre de la racine . Pour l’ essayer on l’écrit à droite du double ( 54) de la racine et on multiplie le nombre
( 543) ainsi formé par le chiffre (3) essayé . On retranche ce produit ( 1629 )
du deuxième nombre partiel ( 1698) . Si
la soustraction ne peut se faire on essaie successivement les chiffres
inférieurs jusqu’à ce que l’on ait trouvé le chiffre exact.
On continue l’opération de la même
manière jusqu’à ce que l’on ait abaissé toutes les tranches .
Le dernier reste ( 1463) est le reste de l’opération.
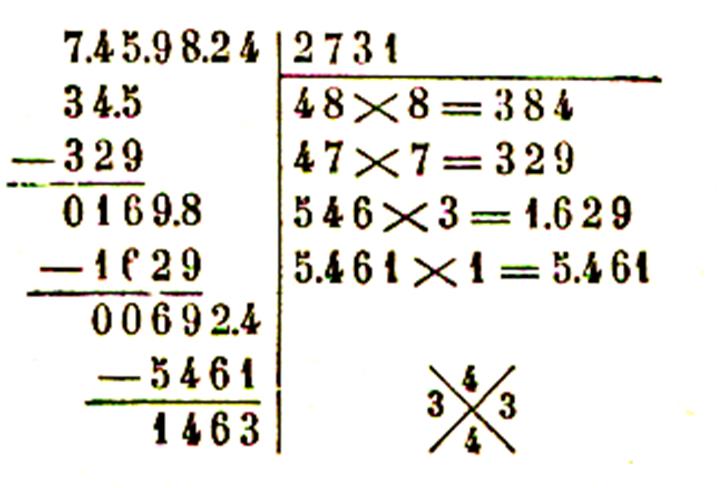
Remarques :
|
1°) Il peut arriver que le quotient
de l’une des divisions soit supérieur à 9 ; dans ce cas on commence les
essaies par le chiffre 9 ( voir ci
contre ) |
|
|
2°) si le quotient est 0 , 0 est le chiffre correspondant de la racine et on
abaisse la tranche suivante à la droite du nombre partiel précédent. (voir
exemple ci contre) |
|
|
3°) Pour former rapidement le double du nombre déjà
trouvé à la racine , il suffit d’additionner les
deux nombres du produit précédent.(voir ci contre) le double de 27 est 47 +7 = 54 2 fois 273 = 543 +3 = 546 |
|
Preuves :
|
7 459 824 = (2731 |
|
|
38 576 = ( 196
donc |
|
|
164 873 = ( 406
donc |
|
Preuves par 9 : on opère comme pour la
division en remarquant que dans ce cas le diviseur et le quotient sont tous deux égaux à la
racine et que le dividende est formé par le nombre ; toute
fois , le reste peut être supérieur à la racine.
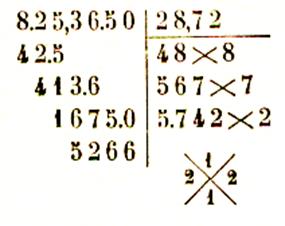
Cas particulier : pour obtenir des chiffres décimaux à la racine , on continue l’opération en abaissant des tranches
de deux zéros .
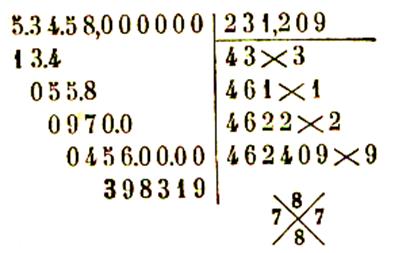
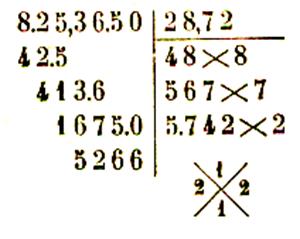
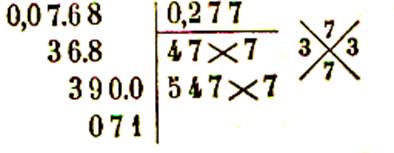
Extraction d’une racine carrée de nombres décimaux :
Pour extraire la racine carrée d’un nombre décimal ,
on extrait d’abord la racine carrée de la partie entière et on continue à abaisser des
tranches de deux chiffres décimaux , les tranches partant de la virgule aussi
bien pour la partie entière que pour la
partie décimale :
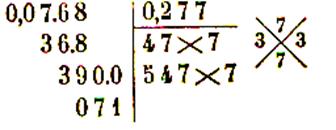
Exemples de calculs :
|
|
|
|
|
|
|
|
|
|
|
|
IV ) Valeur approchée et
encadrement d’une racine carrée
Pré requis : arrondir et troncature
Sur la calculatrice , on lit ![]() = 2,236 067 978 ….
= 2,236 067 978 ….
En général il est inutile de donner toutes les décimales.
Mais on peut affirmer par exemple que : 2,236 < ![]() < 2,237
< 2,237
On dit que l’on a un encadrement de ![]() d’amplitude 0,001 .
d’amplitude 0,001 .
2,236 est une valeur approchée par défaut à 10-3 prés (par excès)de ![]()
2,237 est une valeur approchée par excès à 10-3 prés (par défaut)de ![]()
Plus
généralement :
Si a - 10-n £ x £ a + 10-n
On dit que « a » est une valeur approchée de « x » à
la précision : 10-n
Autres exemples :
|
Encadrement d’amplitude 10-4 de |
Calculatrice :
donc 44,6989£ |
|
Encadrement d’amplitude 10-4 de |
Calculatrice :
donc :
0,2345£ |
3°) « Logarithmes » et « extraction des racines ». ( info ++++)
Les logarithmes fournissent le seul
moyen pratique le seul moyen pratique de calculer une racine d’indice supérieur
à « 2 » .
|
|
Exemple : calculer x = |
|
|
|
|
Log x
= log . |
|
|
|
|
Log x =
|
|
|
|
|
|
Recherche
de Log 620,8 = 2,7930 |
|
|
|
Log x =
|
|
|
|
|
Log x =
0,5586 |
Calculatrice : taper 0,5586
inv. Log = 3,6190951388429760583687708697818 |
|
|
|
D’ où
x = 3,619 |
|
|
|
|
|
|
|
|
|
Nota : lorsqu’un logarithme a une
caractéristique négative , on le divise par un
nombre entier en diminuant la caractéristique et en augmentant la
mantisse d’un même nombre entier ,
choisi de telle sorte que la caractéristique devienne égale au multiple du diviseur qui vient
après la valeur absolue de cette caractéristique dans la suite des nombres. |
|
|
|
|
Exemples :
|
|
|
|
|
Exemple :
calculer : |
|
|
|
|
Log x
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On a vu que toute racine d’un nombre se
traduisait par la division du logarithme de ce nombre par l’indice de la racine .
Exercice : Effectuer la racine
cubique ( x
) de 5 197 ; que l’on écrit : ![]()
On disposera :
x = ![]()
log
x =
![]() log de 5197
log de 5197
Log. X = ![]() log . 5197 ( log
de 5197 = 3 , 71575 )
log . 5197 ( log
de 5197 = 3 , 71575 )
Log x = ![]() ( 3 , 71575
)
( 3 , 71575
)
Log x = 1, 23858
x = 17,32
On recherchera, dans la table, le
nombre correspondant au log. 1,23858 , et l’on
trouvera : 17,32
Qui est la racine demandée.
Avec
la calculatrice , en utilisant la fonction
racine ; on trouve :17,32144978
TRAVAUX AUTO FORMATIFS.
Partie 1
1°) Dites tout ce que
vous savez sur ce symbole:
![]()
2°) Que désigne le
mot « radical » ?
3°) Que désigne le
mot « radicande » ?
Partie
2 :
LES RACINES CARREES.
4°) Donner les trois écritures
utilisées en mathématique pour indiquer que l’on désire connaître la valeur de la racine carrée d’un nombre.(prenez le nombre :
36 )
*on ne vous demande pas de faire le calcul !
5°) Traduire en langage littéral , donner son
utilisation :
"ixe" puissance un sur i grec
![]() ou
ou ![]()
traduire :
: ![]() est
égale
est
égale ![]() est égale
est égale 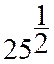
6°)
Que cherche - t - on
à obtenir lorsque
l’on veut connaître la racine carrée d’un nombre ?
7°) Quelles sont les
différentes façons de connaître la racine carré d’un nombre ?
*cela sera
vraie pour tous les cas de recherche de la valeur des
« racines ».
8°) Donnez la procédure
permettant d’obtenir la racine carrée d’un nombre à la calculatrice!
(Il en existe deux
.......).
9°) sous la racine il y a
des nombres séparer par des signes opératoires ; que faut –il faire avant
de rechercher la racine ?
10°) Sous la racine on a
une inconnue , il faudra donc « résoudre » ,
comment faudra t –il procéder pour isoler ?
1° ) Trouver les racines
carrées parfaits des multiples de dixLavec la calculatrice)
de 100 à 10 8
si elles existent ! pour 100 ;101
; 102 ; 103
; 104 ; 105 ; 106 ;10 7 ; 10 8;
2°) soit un
nombre « x » ; trouver la racine carrée du nombre :
x = 7,29 ;
![]() =
=
x = 33,64
; ![]() =
=
x = 81
; ![]() =
=
x = 291 600
; ![]() =
=
x = 2 744 000
; ![]() =
=
x = 1,5746![]() 108 ;
108 ;
![]() =
=
3 ° ) Faire les calculs
suivants à l’aide d’une calculatrice ;donner le résultat avec la précision
du dixième
![]() =
=
![]() =
=
![]() =
=
4 ° ) Faire les calculs
suivants à l’aide d’une calculatrice ;donner le résultat avec la précision
du centième
![]() =
=
![]() =
=
(faire d’abord le calcul sous le radical
)![]() =
=
5 °)
Faire les calculs suivants à l’aide d’une calculatrice ;donner
le résultat avec la précision du millième ((faire d’abord le calcul sous le
radical)
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
6°) Donner, de mémoire, la racine carrée des nombres suivants:
16 ; 36 ;
81 ; 25 ; 49 ;
4 ; 1
; 9 ; 144 ; 121 ;
64 ; 100 ;
7° ) Donner la valeur de
la racine carrée de "2" et de
"3" .:
8°) donner le résultat de la racine carrée des
nombre suivants :
|
|
|
|
|
|
|
|
|
|
|
|
( Résultats dans le cours)
Compléter le tableau suivant : Interdisciplinarité: Les racines en sciences
En
science on utilise l’écriture m1 ; m2 ; dans quelle activité ,
préciser , comment passe-t-on de l’un à
l’autre ?
|
Calcul d’ aire d’un
carré : et inverse |
1° Extraction d’une racine carrée de nombres
entiers
a) Soit donc à trouver la racine
carrée à une unité prés du nombre 68
La
connaissance des carrés des dix premiers nombres nous indique que 68 est compris entre les carrés parfaits 64 et 81
et que par suite sa racine carrée est comprise entre 8 et 9 , c’est à dire que ![]() = 8 à une unité
prés ;
= 8 à une unité
prés ;
64 < 68 < 81
![]() <
< ![]() <
< ![]()
8 < ![]() < 9
< 9
b) le nombre est supérieur à 100 .
Règle : pour extraire la racine carrée
d’un nombre ( exemple 7 459 824 ) entier à une unité
près , on le partage en tranche de deux chiffres à partir de la droite ( 7.45.98.24 ) . Le nombre de tranche , dont la première de gauche ( 7 ) peut n’avoir
qu’un chiffre , est égal au nombre de chiffres de la racine ( 4) . On
dispose l’opération comme une division , les chiffres
de la racine s’inscrivant à la place du diviseur .
On extrait la
racine carrée de la première tranche à gauche ce qui donne le premier chiffre
de la racine ( 2 ) . En retranchant le carré de ce
chiffre ( 4 ) de la première tranche ( 7 ) on obtient le premier reste ( 3 ) à
la droite duquel on abaisse la deuxième tranche ( 45 ) ce qui donne le premier
nombre partiel ( 345 ) On sépare un chiffre à droite de ce nombre ( 34.5 ) et
on divise le nombre de gauche ( 34 ) par le double de la racine ( 4 ) . Le
quotient ( 8 ) ainsi trouvé donne le deuxième chiffre
de la racine ou un chiffre trop fort . Pour l’essayer on l’écrit à droite du
double ( 4 ) de la racine déjà trouvée ( 2) et on
multiplie le nombre ( 48) ainsi formé par le chiffre ( 8 ) essayé . Si le
produit obtenu ( 384) peut se retrancher du premier nombre partiel ( 345 )
le chiffre essayé est exact , sinon ( ce qui est le cas de notre exemple ) on
essaye le chiffre (7) immédiatement inférieur et ainsi de suite jusqu’à ce que
l’on obtienne un produit ( 329 )
inférieur au premier nombre partiel ( 345 ) . On fait la différence ( 345 – 329
) ce qui donne le deuxième reste ( 16 ) à la droite duquel on abaisse la
troisième tranche ( 98 ) pour obtenir le
deuxième nombre partiel ( 1698 ) . On sépare un chiffre à la droite de ce nombre ( 169.8)
et on divise la partie de gauche ( 169 ) par le double de (54) du nombre ( 27)
déjà obtenu à la racine . Le quotient ( 3 ) est
égal ou supérieur au troisième chiffre de la racine . Pour l’ essayer on l’écrit à droite du double ( 54) de la racine et on multiplie le nombre
( 543) ainsi formé par le chiffre (3) essayé . On retranche ce produit ( 1629 )
du deuxième nombre partiel ( 1698) . Si
la soustraction ne peut se faire on essaie successivement les chiffres
inférieurs jusqu’à ce que l’on ait trouvé le chiffre exact.
On continue
l’opération de la même manière jusqu’à ce que l’on ait abaissé toutes les tranches . Le dernier reste ( 1463)
est le reste de l’opération.
Remarques :
|
1°) Il peut
arriver que le quotient de l’une des divisions soit supérieur à 9 ; dans
ce cas on commence les essaies par le chiffre 9 ( voir
ci contre ) |
|
|
2°) si le
quotient est 0 , 0 est le chiffre correspondant de
la racine et on abaisse la tranche suivante à la droite du nombre partiel
précédent. (voir exemple ci contre) |
|
|
3°)
Pour former rapidement le double du
nombre déjà trouvé à la racine , il suffit
d’additionner les deux nombres du produit précédent.(voir ci
contre) le double de
27 est 47 +7 = 54 2 fois 273 =
543 +3 = 546 |
|
Preuves :
|
7 459 824 =
(2731 |
|
|
38 576 = ( 196 donc |
|
|
164 873 = ( 406 donc |
|
Preuves par
9 : on opère comme pour la division en remarquant que dans ce cas le
diviseur et le quotient sont tous deux égaux
à la racine et que le dividende est formé par le nombre ; toute fois , le reste peut être supérieur à la racine.
Cas particulier : pour obtenir des chiffres
décimaux à la racine , on continue l’opération en
abaissant des tranches de deux zéros .
Extraction d’une racine carrée de nombres
décimaux :
Pour extraire la racine carrée d’un nombre décimal , on extrait d’abord la racine carrée de la
partie entière et on continue à abaisser
des tranches de deux chiffres décimaux , les tranches partant de la virgule
aussi bien pour la partie entière que
pour la partie décimale :
Exemples de calculs :
|
|
|
|
|
|
|
|
|
|
|
|