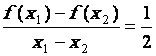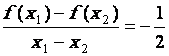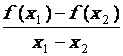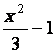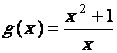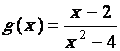Fonction numérique généralités

Pré requis

1°) Notions

2°) Les fonctions (présentation)

ENVIRONNEMENT du dossier:

INDEX warmaths

Objectif précédent

Objectif suivant :

1°) Etude sur l’étude de la représentation graphique d’une fonction

2°) Etude des fonctions usuelles

3°) Retour au cours sur l’étude d’une fonction

Tableau 4.02

Sommaire sur les fonctions.

FONCTIONS NUMERIQUES ( Généralités) :

	· Une fonction numérique est une application d’une partie « D » de « R » dans « R »
	« D » est l’ensemble de définition ( On dit aussi : Domaine de définition) On note F « D » l’ensemble des fonctions d’ensemble de définition « D »
	· Deux fonctions sont gales lorsqu’elles ont même ensemble de définition « D » et qu’elles , donnent la même image de tout élément « x » de « D »

	· Somme de deux fonctions. Soit deux fonctions « f » et « g » ayant le même ensemble de définition « D » leur somme « h = f + g » est définie sur « D » par « h ( x ) = f ( x ) + g ( x ) » L’addition des fonctions est associative et commutative . La fonction nulle est élément neutre.

Info :	· Produit de deux fonctions. Soit deux fonctions « f » et « g » ayant le même ensemble de définition « D » ; leur produit « k = fg » est défini sur « D » par « k ( x ) = f ( x ) .g ( x ) » La multiplication des fonctions est « associative » et « commutative » ; la fonction définie sur « D » : x 1 est « élément neutre » ; la multiplication est distributive par rapport à l’addition…

	· Sens de variation.
	Soit une fonction « f » définie sur un ensemble « E » et « D » un intervalle contenu dans « E ».
Info :	Attention ! il se peut que « f » ne soit ni croissante , ni décroissante sur « D » . Il en est ainsi , sur [ 0 ; 1 ] pour la fonction. x f ( x ) = x ( 1 – x )

	Pour « x ₁ = 0 » , « x ₂ = » , f ( x ₁ ) = 0 , f ( x ₂ ) = et

	Pour « x ₁ = 1 » , « x ₂ = » , f ( x ₁ ) = 0 , f ( x ₂ ) = et

	Le rapport ( appelé parfois « taux d’accroissement ») n’a pas un signe constant pour tous les couples « D² » : F n’est pas monotone.

		Si pour tout couple ( x ₁ ; x ₂) d’éléments distincts de « D »	Alors la fonction « f » est dite :
		0	Croissante sur « D »
		> 0	Strictement croissante sur « D »
		0	Décroissante sur « D »
		< 0	Strictement décroissante sur « D »

	« f » est dite alors monotone ( resp. strictement monotone ) sur « D »

	· Composition de fonctions.
	Soit « f » une fonction définie sur un intervalle D et « g » une fonction définie sur un intervalle « I » et prenant ses valeurs dans D , la fonction composée « h = f o g » est définie sur « I » par « h ( x ) = f [ g ( x ) ]

	Exercices types :
1.	Nommer la fonction ; puis déterminer la plus grande partie de « R » sur laquelle les expressions suivantes définissent une fonction.

	· f (x) = 4 x – 1		Est une fonction affine… elle est définie sur R tout entier.
	· g(x) = x ² - 2 x +1		Est une fonction polynôme ; … elle est définie sur R tout entier.
	· h ( x) =		Est une fonction polynôme ; … elle est définie sur R tout entier.

2.	Nommer la fonction ; puis déterminer la plus grande partie de « R » sur laquelle les expressions suivantes définissent une fonction.
	·		« f » est une fonction rationnelle ; son domaine de définition est donc l’ensemble des réels qui ne donne pas au dénominateur la valeur « 0 » or x R ; x² + 1 > 0 , donc « f » est définie sur « R ».
	·		« g » est une fonction rationnelle ; son domaine de définition est donc l’ensemble des réels qui ne donne pas au dénominateur la valeur « 0 » donc « f » est définie sur « R *». ( x 0)
	·		« h » est une fonction rationnelle ; son domaine de définition est donc l’ensemble des réels qui ne donne pas au dénominateur la valeur « 0 » donc « f » est définie sur « R *». ( x 0 )

3.	Nommer la fonction ; puis déterminer la plus grande partie de « R » sur laquelle les expressions suivantes définissent une fonction.
	·
	·
	·