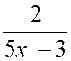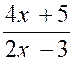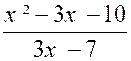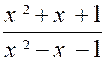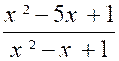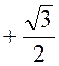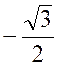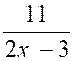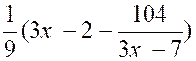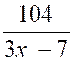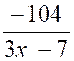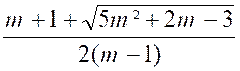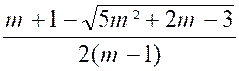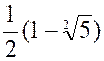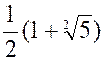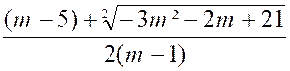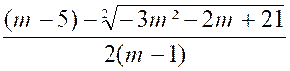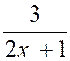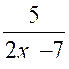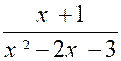- Cours niveau 5 sur le calcul algébrique
	Autres pré requis :( voir « repère cartésien)  ) ;  ( ici : SOS calculs ) ; les symétries

DOSSIER  N° :  Matière :    MATHS Leçon : ETUDE DE <VARIATIONS » de FONCTIONS ( exemples)

Information « TRAVAUX » Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

II ) ENVIRONNEMENT du dossier :

Index  warmaths

Dossier précédent : Revoir «  étude fonction ; ;….. » Fonction généralités.   Représentation type.

Dossier suivant : 1°)Exemples de tracés. 2°) Les fonctions (étude) 3°) Voir l’étude graphique d’une fonction. 4°) Niveau IV (bac prof)

Info : Liste des activités sur l’étude des fonctions.

Leçon	FONCTIONS :
Niveau V ; IV	ETUDE DE variations de QUELQUES FONCTIONS.
Problème 1	Etudier la fonction : y = 4 x ^4 + x² - 3
Problème 2	Etudier la fonction : y = (voir « asymptote » )
Problème 3	Problème 3 : Etudier la fonction y =
Problème 4  :	Etudier la fonction y =
	Méthode indirecte de recherche du maximum ou du minimum.
Problème 5  :	Etudier la fonction y =
	· Méthode indirecte de recherche du maximum ou des minimum.
Problème 6  :	Etudier la fonction y =
	Résumé : comment faire pour étudier les variations d’une fonction donnée.

IV)   INFORMATIONS  «  formation leçon » :

Test	COURS	Travaux  auto - formation.			Corrigé des travaux  auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé  évaluation

COURS

Le but de ce cours est d’ examiner quelques exemples d’études et de les compléter de remarques intéressantes , et qui montera comment il est possible d’anticiper et de vérifier l’exactitude des tracés proposés par les tableurs ou logiciels sont conformes .

Problème 1 : Etudier les variations de la fonction : y = 4 x ^4 + x² - 3 A chacune des valeurs de « x » répond une valeur bien déterminée pour « y » ; cette fonction ne contenant que des puissances paires de « x » , il en résulte que deux valeurs égales , et de signes contraires de « x » donnent à « y » deux valeurs égales , la courbe représentative sera donc symétrique par rapport à la droite «  x = 0 » , ou axe des « y ». Pour la valeur «  x = 0 » la valeur de « y = - 3 » cette valeur est un minimum de « y » , car pour les valeurs de « x » voisines de « 0 » il y a lieu d’ajouter la valeur de « 4 x ^4 + x² » qui est positive. Si nous envisageons l’équation « 4 x ^4 + x² - 3 = 0 »elle n’ admet que deux racines « x’ =  » et « x’ =  », la valeur de « y » ne s’annule donc que deux fois. La valeur de « y » est infinie et positive quand la variable « x » prend l’une des valeurs « +  » ou «- » . On peut résumer les résultats dans le tableau suivant :

Valeur de « x »

«-  »

Croît

0

Croît

« +  »

Valeur de « y »

« +  »

Décroît

0

- 3

0

Croît

« +  »

Il est alors possible de tracer la courbe figurée ci contre

Problème 2 : Etudier la fonction : y =

Cette fonction « y » varie en sens inverse de la fonction linéaire ( 5 x – 3 ) celle-ci est croissante , il en résulte que la fonction proposée est toujours décroissante . La fonction proposée est discontinue pour la valeur « x =   » qui annule le dénominateur ; pour une valeur de « x » un peu inférieure à pour «  x = - » ( «  » étant une quantité très petite ) la fonction est infinie et négative pour une valeur de « x » un peut supérieure pour «  x = + »la fonction est infinie et positive , la valeur de « y » change brusquement de signe en passant par une valeur infinie. D’autre part , pour «  x =  -   » la fonction « y » tend vers zéro par valeurs négatives , pour «  x = +   » tend vers zéro par valeurs positives ; comme valeur particulières observons que pour « x = 0 » , « y =  » . On peut résumer les variations de « y » dans le tableau ci-dessous :

Valeur de « x »

«-  »

Croît

0

-

+

Croît

« +  »

Valeur de « y »

0

Décroît

«-  »

« +  »

Décroît

0

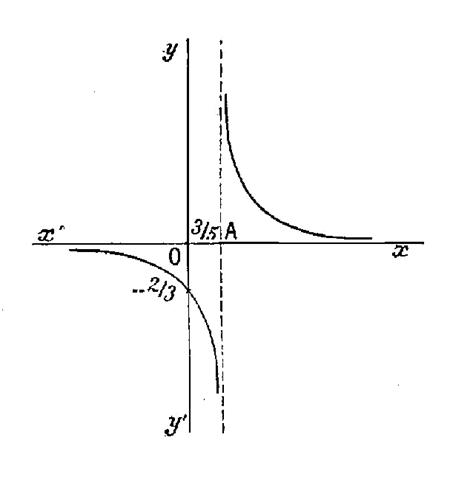
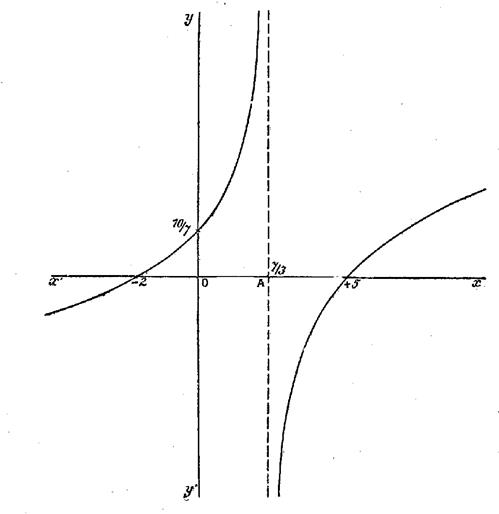
Ces résultats permettent de tracer la courbe indiquée, si cela était nécessaire pour la précision du dessin on calculerait quelques valeurs de « y » répondant à des valeurs arbitraires de « x ». Remarque : La courbe se rapproche indéfiniment de l’axe des « x » sans l’atteindre du côté des « x » négatifs ; de même du côté des « x » positifs. La courbe s’approche également de la parallèle à l’axe de « y » menée par le point A « x =   ». Quand une droite est telle qu’une courbe s’en approche indéfiniment sans l’atteindre , cette droite est dite «  asymptote » de la courbe . · Les asymptotes parallèles à l’axe des « y » s’obtiennent en cherchant les valeurs de « x » qui rendent « y » infini. · Les asymptotes parallèles à l’axe des « x » s’obtiennent en cherchant les valeurs de « y » quand « x » prend une valeur infinie.

Problème 3 : Etudier la fonction y =

En effectuant la division dans le second membre on peut écrire : y = 2 +

Sous cette forme il apparaît que l’étude est analogue à la précédente , il suffit d’ajouter « 2 » aux valeurs de la fraction . La fonction varie en sens inverse de la fonction « 2x-3 » , celle-ci étant croissante la fonction proposée est décroissante. La fonction donnée est discontinue pour la valeur «  x =  » qui annule le dénominateur . Pour «  x =  - »  la fonction « y » est égale à «-  » Pour «  x =  + »  la fonction « y » est égale à «+  » D’autre par pour x = « +  » ou x = «-  » .la valeur de « y » tend vers = 2 comme valeurs particulières observons « y » est nulle pour «  x =  » et que pour « x = 0 » la valeur de « y » est , on peut résumer les variations de « y » dans le tableau ci dessous :

Valeur de « x »

«-  »

Croît

0

-

+

Croît

«+  »

Valeur de « y »

0

Décroît

0

«-  »

«+  »

Décroît

2

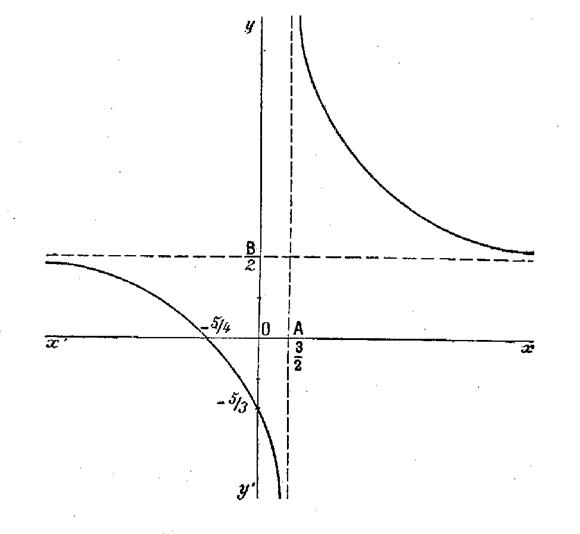
Les résultats ci-dessus permettent de tracer la courbe figurée , celle-ci à une asymptote parallèle à l’axe des « y » , menée par « A » (  ;0) et une asymptote parallèle à l’axe des « x » menée par B ( 0 ; 2 )

Problème 4  : Etudier la fonction y =

En effectuant la division dans le second membre on peut écrire : y =

La première partie de la parenthèse « 3x-2 » est croissante ; l’expression varie en sens inverse de ( 3 x – 7) , mais en changeant le signe et prenant cette dernière expression varie dans le même sens que « 3x-7 » , c'est-à-dire est également croissante , la fonction « y » proposée est donc toujours croissante.

L fonction proposée est discontinue pour «  x =  » qui annule le dénominateur , il est aisé de voir sur l’une ou l’autre les deux formes données a « y » que : Pour «  x =  - » « y » change à «+  » Pour «  x =  +  » « y » change à «-  » D’autre part pour «  x = +  » la valeur « y » est égale à «  = +  » pour «  x = -  » la valeur « y » est égale à «  = -  » comme valeurs particulières observons que « y » est nulle pour «  x’ = -2 » et «  x’’ = 5 » ; enfin pour « x=0 » la valeur de « y » est égale à «  » On peut résumer les résultats obtenus dans le tableau suivant :

Valeur de « x »

«-  »

Croît

-2

0

-

+

+ 5

Croît

+

Valeur de « y »

«-  »

Croît

0

+

-

0

Croît

+

Il est alors possible de tracer la courbe , nous avons déterminé une asymptote parallèle à l’axe « y ».

Méthode indirecte de recherche du maximum ou du minimum.

Nous avons pu, dans les exemples précédents , étudier « directement » les variations des fonctions et déterminer leur maximum et leur minimum .IL n’est pas toujours aisé d’agir ainsi , on peut essayer la « méthode indirecte » qui consiste à opérer de la façon suivante.

Donnant à la fonction « y » une valeur déterminée que nous représenterons par la lettre « m » , on cherche quelle valeur on doit donner à la variable « x » pour que « y » acquière cette valeur « m ». On est ainsi conduit à résoudre une équation « x » , si la résolution de cete équation « x » est possible, la discussion et la détermination des conditions nécessaires pour qu’elle ait des racines donne la limite à imposer à « m » , c'est-à-dire à la fonction « y » , il en résulte par cela même la connaissance du maximum ou du minimum de « y ».

Problème 5 : Soit à étudier la fonction y =

Cherchons la valeur de « x » qui donne à « y » la valeur « m » , on est conduit à résoudre l’équation : m =

Ou : m ( x² - x – 1) = x² + x +1 Soit

m ( x² - x – 1) - x² - x - 1 = 0

m x² - mx – m – x² - x – 1 = 0

( m – 1 ) x² - (m+1) x – ( m + 1 ) = 0

(reste à résoudre l’équation du second degré )

Ce qui donne comme racines :

x ’ =

x ’ ‘ =

Pour que « x » existe il faut que le trinôme sous le radical soit positif , ce qui exige que « m » soit extérieur aux racines «  -1 » et «  » Il faut soit «  m - 1 » , soit «  m  » ; la première condition donne une valeur « -1 » qui est un maximum auquel correspond la valeur « 0 » ; la seconde condition donne un minimum « » auquel répond la valeur «  x = -2 » La fonction ne peut être nulle , mais elle devient infinie en changeant brusquement de signe pour les valeurs de « x » annulant le dénominateur , c'est-à-dire pour :

x’ = = - 0,618

x’ ‘ = = + 1,618

pour x = « +  » ou x = «-  » .la fonction prend la valeur « 1 » ; on peut dresser le tableau des variations

Valeur de « x »

«-  »

- 2

- 0,618

0

+ 1,618

«+  »

Valeur de « y »

1

min

«+  » et «-  »

- 1 max.

«+  » et «-  »

+1

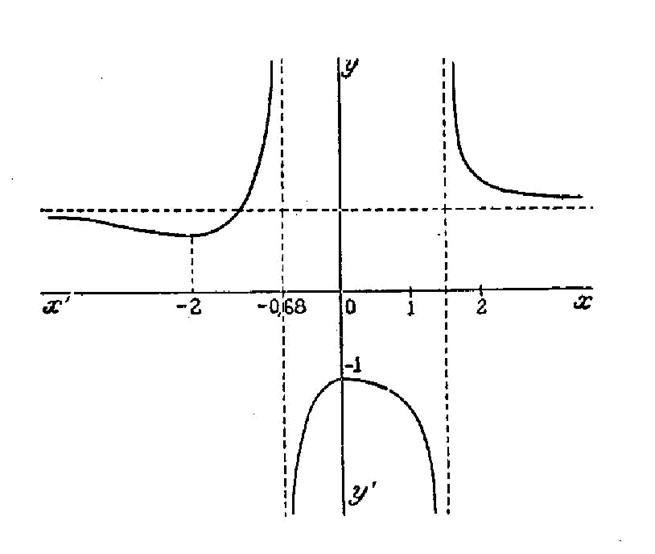
D’où le tracé de la courbe  :

Problème 6 : Etudier les variations de la fonction : y =

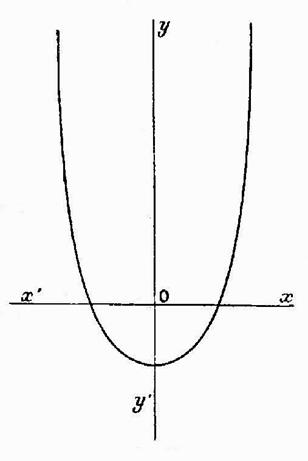
En calculant le discriminant du dénominateur on verra que celui-ci n’a pas de racines. ; la fonction reste donc toujours finie et continue.

Cherchons le maximum et le minimum , en posant : m = D’où : ( m – 1 ) x² - ( m – 5 ) x + ( m-1) = 0

Donnant deux racines :

x’ =

x’’ =

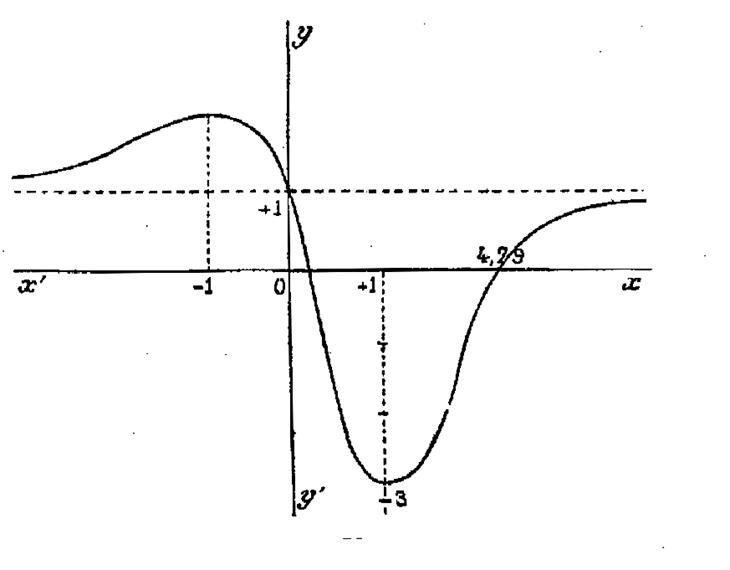
Pour que le trinôme sous le radical soit positif il faut que « m » soit entre les racines « -3 » et «  » : soit « -3 » «  » Ainsi : «  » est un maximum de « y » pour « x = -1 » Et « -3  » est un minimum de « y » pour « x = 1 » La fonction « y » s’annule pour « x² - 5 x + 1 = 0 » ; c'est-à-dire pour : « x’ = 0,21 » et « x’’ = 4,79 »

pour x = « +  » ou x = «-  » .la fonction « y » tend vers « + 1 ». On peut dresser le tableau des variations ci-dessous :

Valeur de « x »

-

- 1

0

0,21

1

4,79

+

Valeur de « y »

+ 1

maxi

+1

0

- 3  mini

0

+ 1

Résumé : comment faire pour étudier les variations d’une fonction donnée ? .

Il résulte des exemples traités que pour étudier les variations d’une fonction donnée il faudra :

1°) Rechercher si la fonction est continue , ou pour quelles valeurs de la variable elle est discontinue , et dans ce dernier cas , examiner comment la fonction se comporte pour des valeurs de « x » voisines de celles qui correspondent à une discontinuité.

2° ) Etudier le sens de variation de la fonction, rechercher si elle est croissante ou décroissante , ou bien présente un maximum ou un minimum. -dans les exemples simples qui ont été étudiés , nous avons pu résoudre aisément ces diverses questions , la méthode directe sera très souvent utile pour rechercher le maximum ou le minimum ; il y a lieu parfois de faire intervenir des méthodes « spéciales » de recherches, qui ne sont pas examinées dans ce cours.

3°) Déterminer les valeurs de la fonction « y » pour certaines valeurs de « x » , en particulier pour les valeurs infinies de « x » , pour les valeurs de « x » annulant la fonction , pour «  x = 0 » , et en général autant de valeurs arbitraires qu’il sera nécessaire pour pouvoir établir le tableau des variations et dessiner la courbe.t

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION  Sur les tracés des fonctions

TRAVAUX  N°    d ’ AUTO - FORMATION : CONTROLE

Donnez la procédure permettant d’étudier la variation d’une fonction.

TRAVAUX N°    d ‘ AUTO - FORMATION EVALUATION

A ) Etudier les variations des fonctions suivantes.

Problème 1	Etudier la fonction : y = 4 x ^4 + x² - 3
Problème 2	Etudier la fonction : y = (voir « asymptote » )
Problème 3	Problème 3 : Etudier la fonction y =
Problème 4  :	Etudier la fonction y =
Problème 5  :	Etudier la fonction y =
Problème 6  :	Etudier la fonction y =

B ) Etudier et représenter graphiquement les variations des fonctions suivantes.

y = 4 x ⁴ + 3 x² - 27

y = 4 x ⁴ - 12 x² + 5

y = 2 x ⁴ - 5 x² + 9

y =

y =

y =