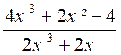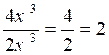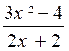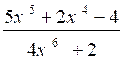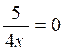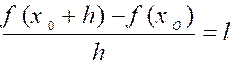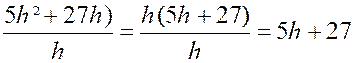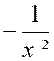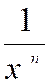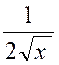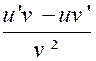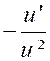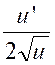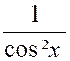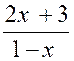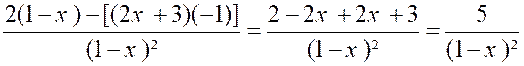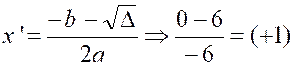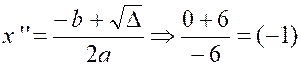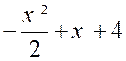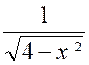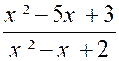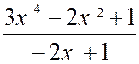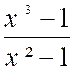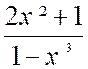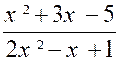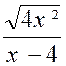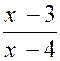Pré requis:
|
Info : liste des
connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES :
liste des cours sur les
études de fonction. |
Complément
d’Info :
·
Liste des cours : prépa concours
|
||
|
|
|
|
|
|
|
|
|
|
|
|
TITRE :PREPARATION CONCOURS niveau VI ; V ; IV ; ETUDE de FONCTIONS - APPLICATIONS
12 : FONCTION
·
12.1
– Fonction – Définition.
·
Fonction numérique –
Définition
·
12 . 3
Application - définition
·
12 . 4 Applications
particulières : SURJECTION – INJECTION – BIJECTION
13 – ETUDE D’
UNE FONCTION NUMERIQUE .
·
1°)
Recherche du domaine de définition
·
2°) Recherche des limites aux
bornes du domaine de définition
………………Continuité .en 1 point
…………….Continuité sur un
intervalle…….
·
4°) Calcul des extremums locaux .
·
5°) Graphique
Travaux ; devoirs
|
|
Corrigé du :
|
|||
|
|
Contrôle |
évaluation |
|||
|
|
|
|
|
|
|
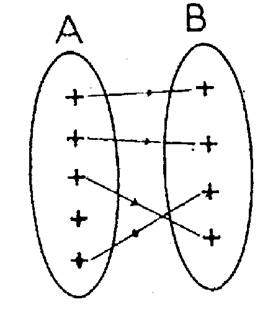
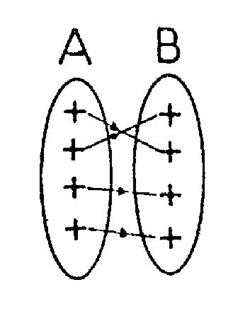
12.1 – FONCTION
– DEFINITION . On appelle
fonction de A vers B toute relation qui à chaque
élément « x » de A , associe au plus un élément « y » de B . |
|
|
|
|
|
« « y »
s’appelle la valeur ( ou l’image de « A est
l’ensemble de départ . B est
l’ensemble d’arrivée Notation : f : A® B x a
f (x) où y = f (x) |
|
12 .2 Fonction numérique – Définition
C’est une
fonction pour laquelle les ensembles de départ et d’arrivée sont des parties de
R
(réels)
12 . 3 Application
- définition
Une
application de A vers B est une
fonction de A vers B telle qu’ à chaque « x » de A il corresponde un élément
unique « y » de B.
|
Ensemble ou domaine de définition : c’est
l’ensemble des « x » qui ont une image ( D f ) L’ensemble
de départ correspond avec le domaine
de définition . |
|
Exemple : (dont les études de
fonctions)
info plus sur la fonction dite homographique .
c'est-à-dire soit la fonction f qui a « x »
associe ![]()
Ensemble de définition :
La fonction f est définie pour tout « x »
différent de 0 . car si x= 0 , on ne peut pas calculer ![]()
Df = R - ![]() ou R* ou ] - ¥ ; 0 [ U ] 0
; +¥
[
ou R* ou ] - ¥ ; 0 [ U ] 0
; +¥
[
Notation :
f : R *® R
x a
![]()
f (x)=
![]()
12 . 4 Applications particulières : SURJECTION – INJECTION – BIJECTION
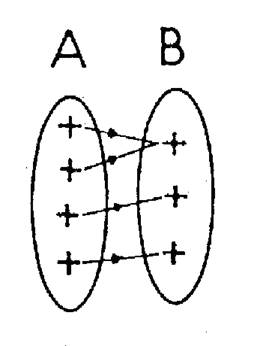
12.4.1 : Surjection - définition :
|
Une
application f de A dans B est dite
« surjective » si chaque élément de « B » est l’image
d’un élément au moins de A . |
|
A tout
élément de B aboutit au moins une flèche
.
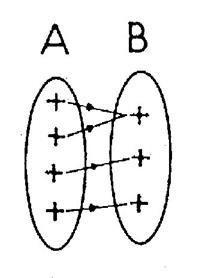
12.4 .2 : Injection - définition :
|
Une
application f de A dans B est dite
« injective » si chaque élément de « B » est l’image d’un
élément au plus de A . |
|
A tout
élément de B aboutit au plus une flèche .
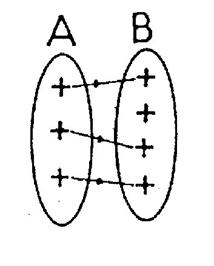
12.4 .3 : Bijection - définition :
|
Une
application f de A dans B est dite
« bijective » si chaque élément de « B » est l’image d’un
élément unique de A . |
|
13 – ETUDE D’UNE FONCTION NUMERIQUE .
Marche à suivre pour étudier une
fonction :
1°) Recherche du domaine de définition
2°) Recherche des limites aux bornes du
domaine de définition
3°) Calcul de la dérivée pour déterminer les
divers sens de variation de la fonction ( tableau de
variation)
4°) Calcul des extremums locaux
5°) Graphique
Etudier la définition d’une fonction numérique , c’est déterminer pour quelques valeurs la
variable ( x) il est possible de calculer la valeur numérique
correspondante de la fonction (y).
En étudiant la définition d’une fonction , on
définit le domaine de définition de cette fonction.
Notation : D f ( si la fonction est
notée f )
Il est
nécessaire de déterminer le domaine de définition d’une fonction dans 4 cas ; ( dans les autres cas
le domaine sera R ) .
a) pour une fonction du type : f (x) =
![]() ou ( m est un polynôme ) ;
m doit être différent de 0 ,
donc toutes les valeurs de « x » qui annulent m
doivent être chassées.
ou ( m est un polynôme ) ;
m doit être différent de 0 ,
donc toutes les valeurs de « x » qui annulent m
doivent être chassées.
Exemple : f(x) =
![]() 4x + 5 =
0 Û x =
4x + 5 =
0 Û x = ![]()
D f = ]
- ¥ ;
![]() [ U ]
[ U ] ![]() ; +¥
[ ou = R
; +¥
[ ou = R ![]()
b) Pour une fonction du type f (x) = ![]() ; m doit être positif ,
donc ³
0 ( car une racine carrée ne peut être négative ) .
; m doit être positif ,
donc ³
0 ( car une racine carrée ne peut être négative ) .
Exemple : f (x) = ![]() ; 4x+5 ³ 0 Û x ³
; 4x+5 ³ 0 Û x ³ ![]()
Df = [![]() ; +¥ [
; +¥ [
c) Pour une fonction tangente ou cotangente ( voir trigonométrie )
d)
Exemple : f (x) = 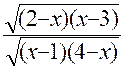
pour que cette fonction soit définie , il faut que :
(2-x) (x – 3) ³
0 et ( x-1) (4-x) ³
0
Pour trouver les valeurs de « x »
qui rendent positives ces polynômes , on
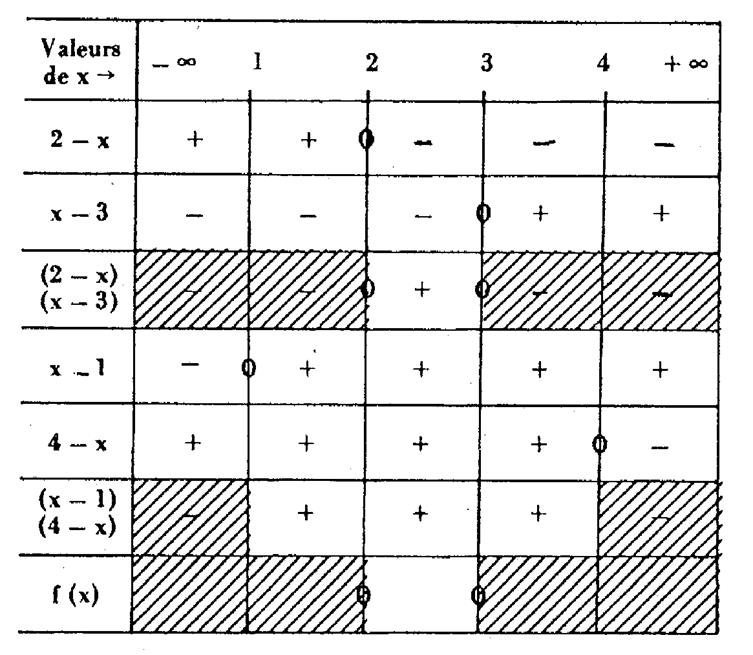
utilisera un tableau :
|
2-x
³
0 Û x £ 2 |
x-1>
0Û x > 1 |
|
x-3
³
0 Û x ³ 3 |
4-x
> 0Û x < 4 |
Les zones hachurées correspondent aux valeurs
de « x » qui sont exclues du domaine de définition (
car elles rendent le polynôme
sous le radical « négatif »)
La dernière ligne hachurée
, représente la superposition des
2 zones précédentes et permet de déterminer dans quel intervalle , les valeurs
de « x » ne rendront jamais les 2 polynômes négatifs.
Solution : D f
= [ 2 ;
3 ]
Tableau
de variation :
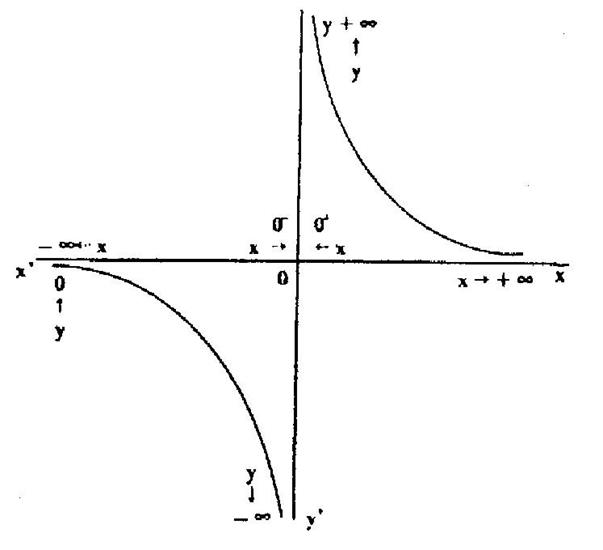
13 . 2 .- Limites
Exemple
soit la fonction ![]()
D f =
R - ![]() ou
R* ou
] - ¥ ;
0 [ U ] 0 ; +¥ [
ou
R* ou
] - ¥ ;
0 [ U ] 0 ; +¥ [
Traçons la représentation graphique de cette
fonction :
|
On remarque que : Quand « x » diminue
, « y » tend vers 0 Þ
lim f(x) = 0 ; Quand « x » augmente , y tend vers 0 lim f(x) = 0 ; x®+¥ Quand x tend vers 0 par valeur
inférieure : y
tend vers -¥
, lim f(x) = -¥ ;
x ®0- Quand x tend vers 0 par valeur
supérieure : y
tend vers +¥
, lim f(x) = +¥ ;
x ®0- |
|
Nous
remarquons que l’étude des limites se fait au voisinage des bornes de
l’ensemble de définition.
Opérations sur les limites
Limite d’une somme .
- Lorsque x tend vers x0 ou vers ±¥
|
Si f(x) tend vers Et si
g (x) tend vers : |
a b |
a +¥ |
a -¥ |
+¥ +¥ |
-¥ -¥ |
+¥ -¥ |
|
f(x) + g(x) tend vers |
a+
b |
+¥ |
-¥ |
+¥ |
-¥ |
? |
Limite
d’un produit .-
Nous
supposons connu le signe de chacun des facteurs
f(x) et g (x) et nous donnons
seulement la valeur absolue de ces facteurs ou de leur produit lorsque cette
valeur absolue est infinie .
|
Si
f (x) tend vers Et si
g (x) tend vers : |
a b |
a ¹ 0 ¥ |
|
¥ ¥ |
|
0 ¥ |
|
f(x) |
a b |
¥ |
|
¥ |
|
? |
Limite d’un quotient .
- En supposant connu le signe de chacun des termes f(x) et g(x) , nous ne donnons
que leur valeur absolue ou celle de leur quotient lorsque cette valeur absolue
est infinie . Lorsque « x » tend vers x0 ou vers ±¥
|
Si
f (x) tend vers Et si
g (x) tend vers : |
a b ¹ 0 |
±¥ b ¹ 0 |
a ¹ 0 0* |
a ¥ |
0 0 |
¥ ¥ |
|
|
|
¥ |
¥ |
0 |
? |
? |
·
Rechercher la limite d’un polynôme lorsque
« x » tend vers + ou - l’infini ,équivaut à rechercher la limite du terme du plus
haut degré lorsque x ®±¥
Exemples :
N°1 :
|
|
lim. 2 x3 + 4 x² + 2x – 4 |
|
lim 2 x3
= +¥ |
(à vérifier avec la calculatrice graphique) |
|
|
x ®+¥ |
|
x ®+¥ |
|
N°2 :
|
|
lim.
3 x5 + 4 x4
+ 2x – 4 |
|
lim 3 x5 = - ¥ |
(à vérifier avec la calculatrice graphique) |
|
|
x ® - ¥ |
|
x ® - ¥ |
|
·
La limite d’une fonction rationnelle,lorsque “x” devient infini ,est celle du quotient des
termes de plus haut degré de son numérateur et de son dénominateur.
Exemples :
La limite d’une fonction rationnelle,lorsque “x” devient infini ,est celle du quotient des
termes de plus haut degré de son numérateur et de son dénominateur.
Exemples :
N°1 :
|
|
lim. |
|
lim |
(à vérifier avec la calculatrice graphique) |
|
|
x ®+¥ |
|
x ®+¥ |
|
N°2 :
|
|
lim. |
|
|
(à vérifier avec la calculatrice graphique) |
|
|
x ®-¥ |
x ®-¥ |
x ®-¥ |
|
N°3 :
|
|
lim. |
|
lim |
(à vérifier avec la calculatrice graphique) |
|
|
x ®+¥ |
x ®+¥ |
x ®+¥ |
|
a) Continuité
en 1 point.
Soient
x0 ; a ; b ; des réels tels que a < x0
< b. On considère une fonction f définie sur un ensemble D contenant ]a ; b [.
On dit que f est continue en x0 si
et seulement si :
- la limite quand x tend vers x0 existe
- lim f = f (x0 )
-
x ® x0
cela
équivaut à
|
|
lim f
= |
lim f
= |
lim f (x0 ) |
|
|
|
|
|
|
|
Exemple : soit f(x) = 2 x² + 4 x + 5 ; continuité en x0 = 1
|
|
lim f = 2 (1)² + 4 x1+ 5 = 11 |
|
lim
f existe |
|
|
|
x ® 1 |
|
x
®
1 |
|
|
|
f (x0)
= 11 |
|
lim f
= f (x0) |
|
|
|
|
|
x
®
1 |
|
|
|
|
|
|
|
|
|
|
|
la fonction est continue en x0
= 1 |
|
b) Continuité sur un intervalle.
On
dit que f est continue sur ]a ;b[ si f est continue en tout x0
élément de ]a ;b[
D’où les théorèmes :
-
Toute fonction polynôme est continue
sur R
-
Toute fonction rationnelle est
continue sur son domaine de définition.
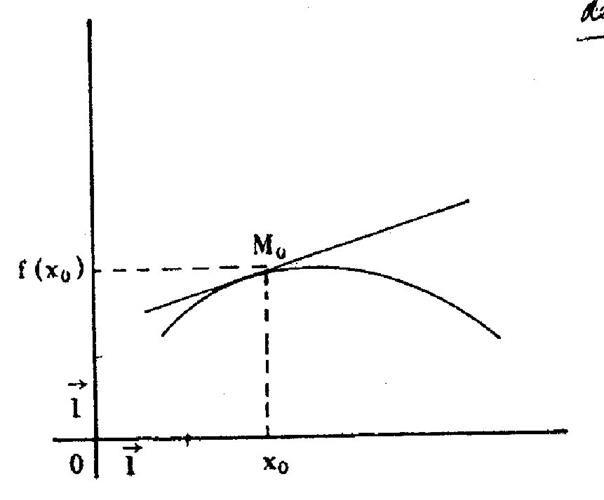
A) Dérivée en un point .
· Soit
x0 , un élément d’un intervalle ]a ;b[
. On considère une fonction , f définie sur un
ensemble D contenant ]a ;b[ . Soit . On appelle h un réel
, on appelle « dérivée « de f
pour x = x0 la limite
( si elle existe) du rapport : 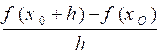 quand h tend vers 0 .
quand h tend vers 0 .
|
|
lim |
|
|
|
|
|
h ® 0 |
|
|
|
Notation : y’0 ou f ’ (x0)
Interprétation
graphique :
|
Pour qu’une fonction y = f(x) admette en x0
une dérivée, il faut et il suffit que la courbe représentative admette au
point d’abscisse x0 une tangent (non parallèle à y0.) Le coefficient directeur de cette
tangente est égal à la dérivée de la
fonction pour x = x0 Equation de la tangente : y = f ’ (x0) . ( x – x0) + f (x0) Remarque :
f ’ (x0) est la dérivée…… |
|
Exemple :Soit la fonction f(x) = 5 x² + 7 x + 4
Questions :
· Trouver
la dérivée au point xO = 2
· Déterminer
l’équation de la tangente.
|
Calcul de la dérivée au point xO
= 2 |
|
|
|
|
Calcul de
f (x O) pour x O = 2 ; ·
f
(2) = 5 (2 )² + 7 (2) + 4 ·
Soit 20 + 14 + 4 = 38 |
Calculatrice : taper : [ 5 (2 )² ] + [ + 7 (2)] + ( + 4) |
|
|
|
|
|
|
Calcul de
f (x O + h ) ; avec
x O = 2 ·
f
(2 + h ) = 5 (2 + h )² + 7 (2 + h ) + 4 |
(2 + h )²
= (2 + h ) (2
+ h ) = 4 + 2 h + 2 h + h² = 4 + 4 h +
h² = 5 ( 4 + 4 h + h²
) =
20 + 20 h + 5 h² |
|
|
·
f
(2 + h ) = 20 + 20 h + 5 h² + 14 + 7 h + 4 = 5 h² +27 h + 38 |
|
|
|
|
|
|
|
Calcul de
f (x O + h ) - f (x O) = ·
= 5 h² +27 h + 38 - 38 ·
= 5 h²
+27 h |
|
|
|
|
|
|
|
Calcul de |
|
|
|
|
|
Ainsi :
|
|
lim |
5 h + 27
|
|
= 27 |
|
|
h ® 0 |
|
|
|
Lire :
la limite de 5 h + 27 quand
« h » tend vers 0 est
égale à « 27 »
|
l’équation
de la tangente. |
|
||||||||||||||
|
|
y
= 27 ( x – 2
) + 38
= 27 x – 54 +38 y
= 27 x – 16 |
|
|||||||||||||
|
|
Nota : « dérivée et
continuité » Si la fonction « f » admet une dérivée en x O ( la réciproque n’est
pas vraie ) |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
13.4.2
– Fonction dérivée d’une fonction. |
||||||||||||||
|
|
Soit « f » une fonction admettant
une dérivée « f ’ (xO) » pour
toute valeur xO d’un intervalle ]
a , b [ ; la fonction qui a tout xO
de ] a , b [ associe le nombre dérivée « f’ (xO) »
s’appelle « fonction dérivée ». |
|
|||||||||||||
|
|
Notation :
« f ’» Par abus de langage, on dit souvent
« dérivée » au lieu de « fonction dérivée » |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
Valeur
de la fonction « f ( x) » |
Valeur de la fonction dérivée « f ‘( x) » |
|
|
||||||||||
|
|
|
C (constante) |
0 |
|
|
||||||||||
|
|
|
x
|
1 |
|
|
||||||||||
|
|
|
x² |
2
x |
|
|
||||||||||
|
|
|
x3 |
3
x² |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
x
n ; ( n |
n
x n-1 |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
fonction |
Dérivée |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
u
+ v |
u
’ + v ‘ |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
k
u ( k : constante) |
k
u ’ |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
u
+ v |
u
‘ v
+ u v ‘ |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
u
² |
2
u . u’ |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
u
3 |
3
u ² . u’ |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
Autres
dérivées. |
Fonction ; « f ( x) » |
Dérivée : « f ‘( x) » |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
Sin
x |
Cos
x |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
Cos
x |
-
sin x |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
Tan
. x |
|
|
|
||||||||||
|
|
|
|
|||||||||||||
|
|
Exemples : Calculer
les dérivées des fonctions suivantes : |
|
|||||||||||||
|
N°1 |
«
f ( x) »
= 3 x 4 + 2 x² + 3 x + 4 |
||||||||||||||
|
|
« f ‘( x) » = 4 fois
3 4-1 + 2 fois 2 x 2-1 + 3 |
f ‘( x) = 12 x 3 + x + 3 |
|||||||||||||
|
N°2 |
«
f ( x) »
= ( x – 1 ) 3 ( x +
2 ) 4
; |
|
|||||||||||||
|
|
est
de la forme u . v = u ‘
v + u v ‘ |
|
|||||||||||||
|
|
Calcul
de « u ‘ » |
|
|||||||||||||
|
|
U = ( x – 1 ) 3 , ou
U = Donc
u’ = 3 |
|
|||||||||||||
|
|
Calcul
de « v ‘ » |
|
|||||||||||||
|
|
V = ( x + 2 ) 4 ;
ou V = v 4 avec v = x + 2 |
|
|||||||||||||
|
|
Donc
V ’ = 4 v3 v ’ =
4 ( x + 2 ) 3 ; car v ’ = 1
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
On a alors : y ‘
= f ‘( x) = U V’ + V U’ |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
U V’ + V U’
= ( x – 1 ) 3 fois 4 ( x + 2 ) 3 + ( x + 2 ) 4 fois 3 (
x – 1 ) ² |
|
|||||||||||||
|
|
= ( x – 1 ) ² ( x + 2 ) 3
[ 4 ( x – 1 ) + 3 ( x + 2 ) ] |
|
|||||||||||||
|
|
y ‘ = ( x
– 1 ) ² ( x + 2 ) 3 ( 7 x + 2 ) |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
13 . 4 . 3. – Signe de la
dérivée et sens de variation de la fonction. |
|
|||||||||||||
|
|
Suivant le signe de la dérivée, on peut
déterminer le sens de variation d’une fonction : -
Si la dérivée est nulle
, la fonction est constante. -
Si la dérivée est positive dans un
intervalle ] a ,
b [ , la fonction est croissante dans cet intervalle. -
Si la dérivée est négative dans un intervalle ] a , b [ , la
fonction est décroissante dans cet intervalle. |
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Un extremum local est un point qui va déterminer où la
fonction va passer d’un accroissement
à une diminution (
ou inversement : la fonction
va passer d une diminution à’un accroissement ) |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
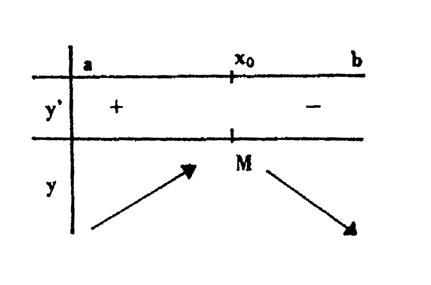
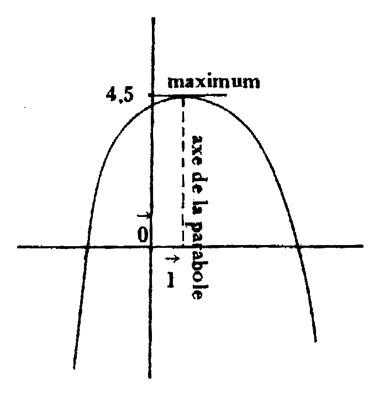
|
-
Maximum
local : ( M ) Une fonction a un
maximum local pour x O si elle cesse de croître pour décroître
quand « x » traverse , en augmentant , la valeur x O ,donc si sa dérivée change
de signe pour x = x O en passant du positif au négatif . |
||||||||||||||
|
|
Tableau
de variation type |
Représentation
graphique de la fonction. |
|||||||||||||
|
|
|
|
|||||||||||||
|
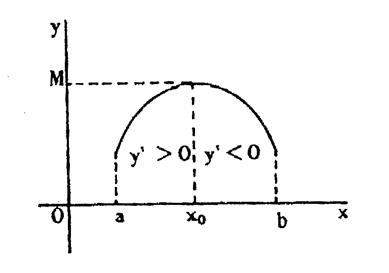
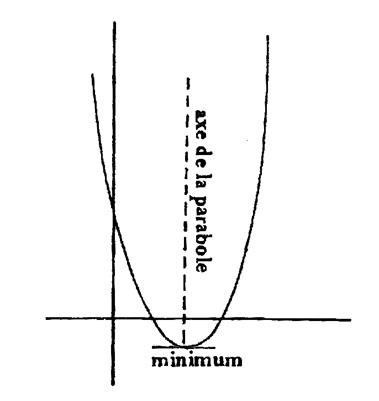
|
-
Minimum
: ( m ) Une fonction a un
minimum local pour x O si elle cesse de décroître pour croître
quand « x » traverse , en augmentant , la valeur x O ,donc si sa dérivée change
de signe pour x = x O en passant du négatif au positif. |
||||||||||||||
|
|
Tableau
de variation type |
Représentation
graphique de la fonction. |
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Pour déterminer les extremums locaux, il
faut rechercher pour quelles valeurs de « x » la dérivée s’annule. |
||||||||||||||
|
|
13 . 4 . 4. – Tableau de variation. |
||||||||||||||
|
|
Procédure à suivre pour établir un tableau
de variation : |
||||||||||||||
|
|
1° ) Calculer la
ou (les) dérivée de la fonction . 2°) Rechercher pour quelle valeurs de
« x » cette dérivée s’annule. 3°) Déterminer, par rapport à ces valeurs , les zones où la dérivée est positive ou
négative. 4°) Dresser le tableau. |
||||||||||||||
|
|
|
||||||||||||||
|
|
Exemple 1 : Construire le tableau de variation de la
fonction f(x) = |
||||||||||||||
|
|
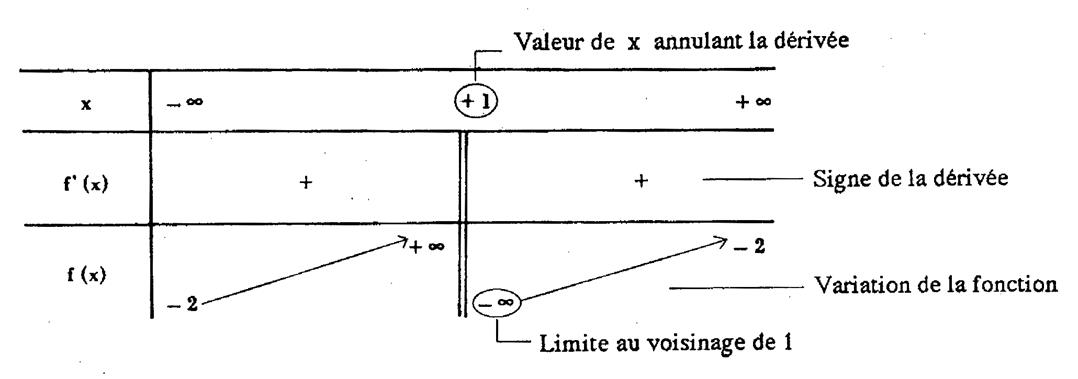
Info : f(x) = |
||||||||||||||
|
|
Calculs des dérivées des termes
u et v :, u’ = 2
; et v ’ = -1 |
||||||||||||||
|
|
Calcul de la dérivée de la fonction : f ‘ (x) = |
||||||||||||||
|
|
5
> 0 et ( 1- x )² |
||||||||||||||
|
|
|
||||||||||||||
|
|
Exemple 2 : Construire le tableau de variation de la
fonction f (x) = - x 3 + 3 x – 2 |
||||||||||||||
|
|
Calcul de la dérivée de la fonction :
f ‘ (x) = - 3 x² + 3 ; f ‘ (x)
est de la forme ax² + bx + c ; nous
devons calculer le discriminant ( |
||||||||||||||
|
|
On pose : - 3 x² + 3 = 0 |
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
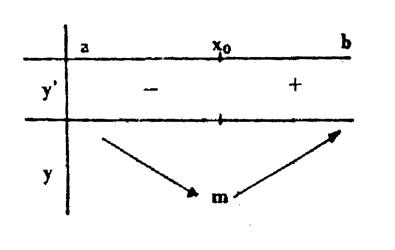
Dans le cas d’une dérivée de la forme ax² +
bx + c , elle admet 2 solutions pour f ‘ (x) = 0 , la
dérivée est : -
« négative » entre les racines si a > 0 -
« positive » entre les racines si a
< 0 |
||||||||||||||
|
|
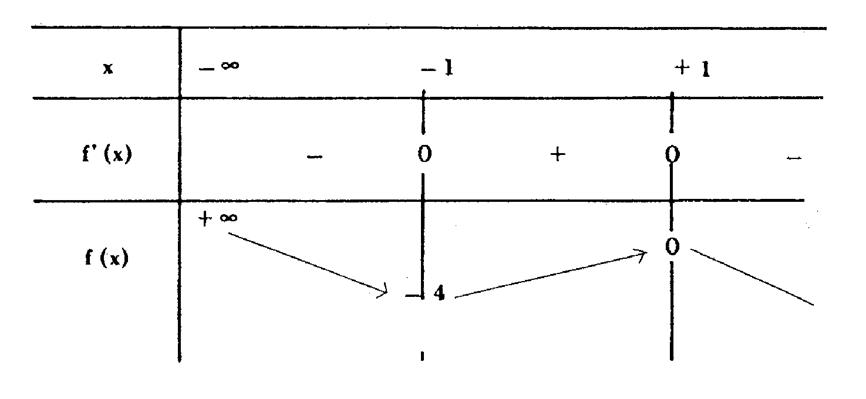
Soit
le tableau de variation : |
||||||||||||||
|
|
|||||||||||||||
|
|
NOTA : Le tableau de
variation va nous donner une représentation schématique du graphique de la
fonction. On pourra , grâce
à ces données , tracer une courbe de la fonction étudiée et la rendre plus
précise avec quelques points dont on aura calculé les coordonnées. |
||||||||||||||
|
|
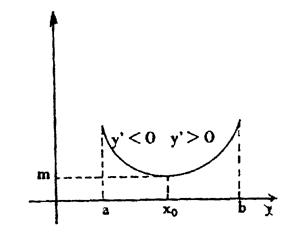
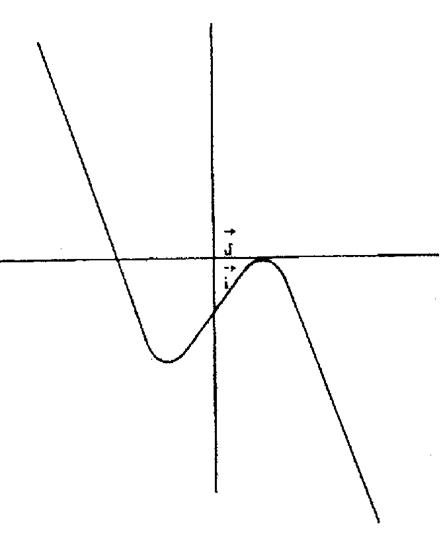
Reprenons l’exemple précédent : Dans
le tableau de variation de la fonction
f (x) = - x 3 + 3 x
– 2 Grâce au tableau ,
nous voyons que : -
Sur l’intervalle ]
- -
Sur l’intervalle ]
– 1 ; + 1 [
la fonction décroissante f (x)
allant de ( - 4 ) à 0 -
Sur l’intervalle
]+1 ; + |
||||||||||||||
|
|
La
courbe représentative de la fonction sera donc : ( à
vérifier avec une « graphique ») |
||||||||||||||
|
|
|
||||||||||||||
|
|
13
. 4 . 6. – Représentations graphiques de divers fonctions types . |
||||||||||||||
|
Nota : Les représentations graphiques
se feront dans un repère orthonormé. |
|||||||||||||||
|
|
Cas
particulier de la fonction affine….. |
||||||||||||||
|
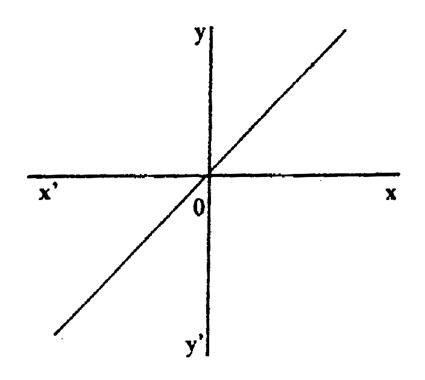
FONCTION LINEAIRE : |
|||||||||||||||
|
|
-
type : y = a x -
« a » est appelé le
coefficient directeur ou coefficient de proportionnalité. -
La courbe d’une fonction linéaire ( droite) passe
toujours par le point O de coordonnée
( 0 ; 0 ) -
Le domaine de définition : D f = R |
||||||||||||||
|
|
|
|
|||||||||||||
|
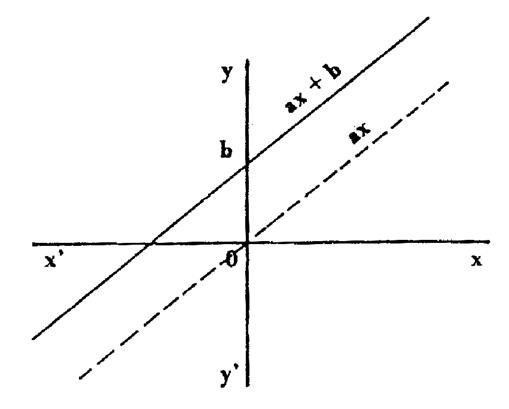
LA FONCTION AFFINE ; |
|||||||||||||||
|
|
-
type : y = ax + b
-
Sa représentation graphique est une
parallèle à la Courbe de la fonction y= ax. -
Elle passe toujours par le
point ( 0 ;
b ) -
Le domaine de définition : D f = R |
|
|||||||||||||
|
LA
FONCTION POLYNOMIALE. |
|||||||||||||||
|
|
-
type : y = ax² + bx + c -
La courbe de cette fonction est une parabole. -
Note :Les
fonctions du type f (x) = a x² ont la même forme de courbe. -
Le domaine de définition : D f = R |
|
|||||||||||||
|
|
Exemple : a > 0 |
Exemple : a < 0 |
|||||||||||||
|
|
|
|
|||||||||||||
|
|
y
= |
y
= x² - 4 x + 3 |
|||||||||||||
|
|
|
||||||||||||||
|
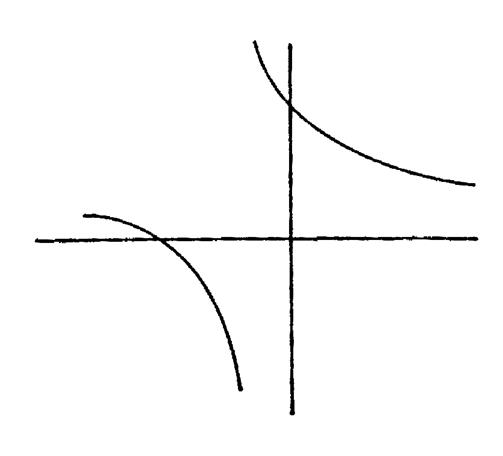
LA FONCTION RATIONNELLE . |
|||||||||||||||
|
|
-
Type : -
Le domaine de définition : D f est l’ensemble de tous les « x »
n’annulant pas le dénominateur. -
La courbe d’équation y = Elle est similaire à la courbe
d’équation y = |
|
|||||||||||||
|
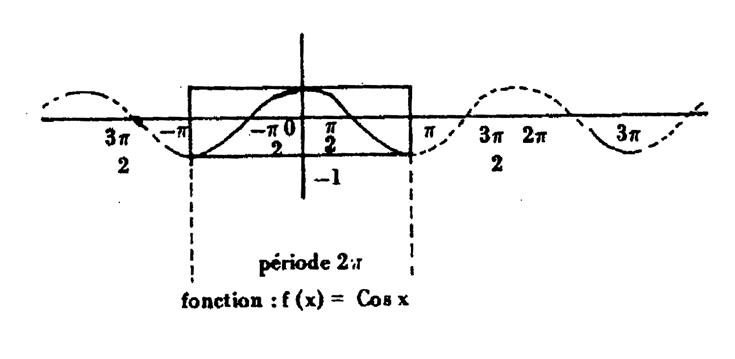
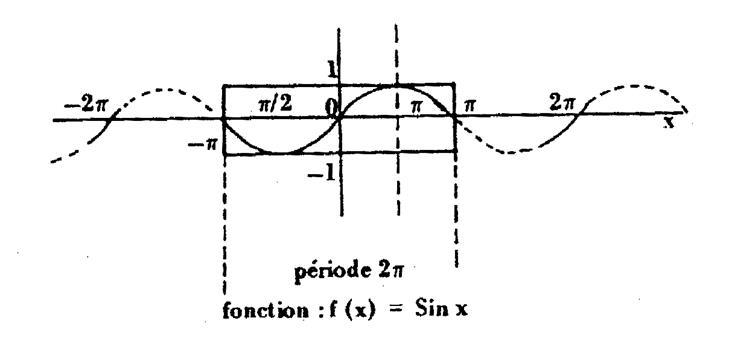
REPRESENTATION GRAPHIQUE DES FONCTIONS
CIRCULAIRES. |
|||||||||||||||
|
|
Les fonctions sinus ; cosinus , tangente
et cotangente sont des fonctions périodiques ( période 2 |
||||||||||||||
|
|
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|||||||||||||
|
|
TRAVAUX AUTO FORMATIFS. |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
CONTROLE |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
EVALUATION :
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Voir le cours. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Déterminer
l’ensemble de définition de : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
1°) f (x) =
2 x² + 4 x – 5 |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
2°) f (x) =
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
3°) f (x) =
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Traduire
et Calculer les limites suivantes : |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
1°) lim 5 x² -
2x+4 |
|
|||||||||||||
|
|
x |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
2°) lim ( 3 x² - 2x – 1 ) |
|
|||||||||||||
|
|
x |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
3°) lim ( 2 x 3 + x + 1 ) |
|
|||||||||||||
|
|
x |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
4°) lim |
|
|||||||||||||
|
|
x |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
5°) lim. |
|
|||||||||||||
|
|
x |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
6°) lim. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Calculer
les fonctions dérivées des fonctions suivantes : |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
a)
f (x) = |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
b) f (x) =
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
c) f (x) =
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Faire le tableau de variation et tracer la
courbe représentative de la fonction : |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
f (x) =
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||