PRE REQUIS DOSSIER
: LES FONCTIONS N°1
Etude de la représentation graphique d’une FONCTION NUMERIQUE.( généralités )
|
|
|
|
|
|
Corrigé
évaluation : |
Intérêt : savoir étudier un tracé dans des
matières interdisciplinaires (physique,chimie ,
géographie, histoire, statistique,….)
TRAVAUX AUTO FORMATIFS.
CONTROLE:
1°) Sur quelles caractéristiques peut porter
l’étude de la représentation graphique d’une fonction ?
(Préciser pour chaque
caractère)
|
|
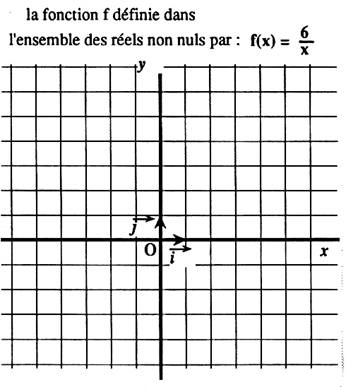
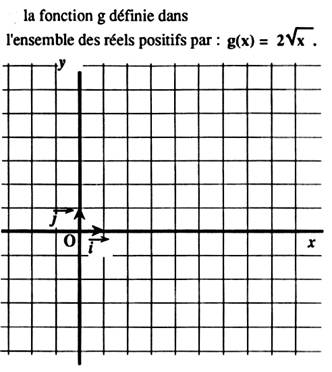
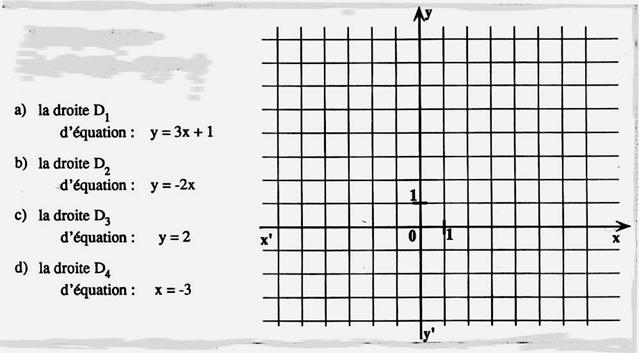
N°1 : Utiliser les quadrillages pour représenter graphiquement les fonctions
suivantes : |
|||
|
|
|
|
|
|
|
|
Donner le sens de
variation des fonctions « f » et « g » sur les
intervalles indiqués, en complétant les phrases suivantes : Sur [ 1 ; 6 ] ; « f » est une fonction ……………………………………………. Sur [ 0 ; 5 ] ;
« g » est une fonction ……………………………………………… Toujours à propos des
fonction « f » et « g » , dans chacun des cas ci -
dessous, entourer la réponse qui convient et barrer l’autre : Pour les petites
valeurs positives de « x » ,
f(x) prend des : Pour les grandes valeurs
positives de « x » , f(x) prend des : Pour les grandes
valeurs positives de « x » ,
g(x) prend des : |
|||
|
|
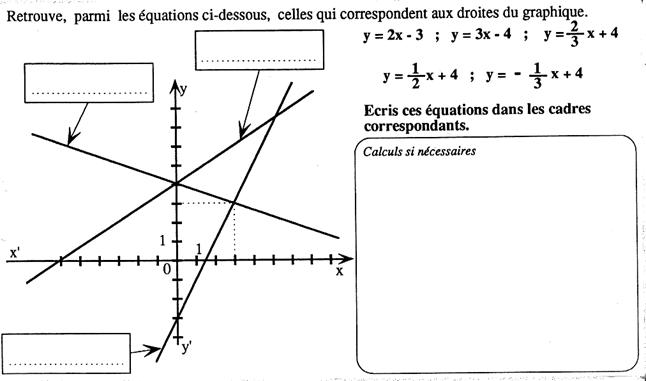
N°2 ( SOS Corrigé) |
|
|
|
|
|
|
|
N°3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
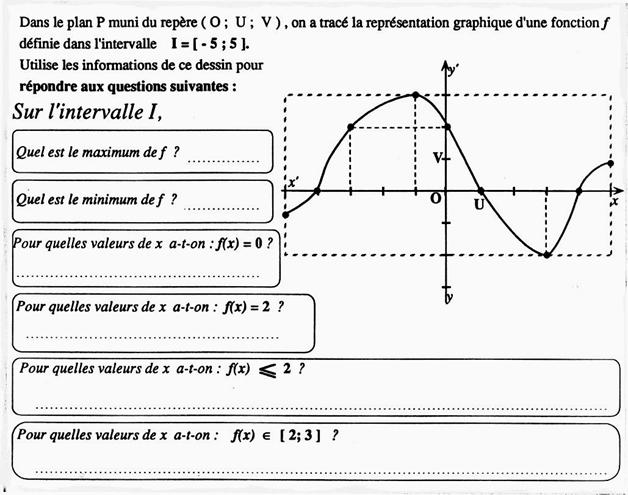
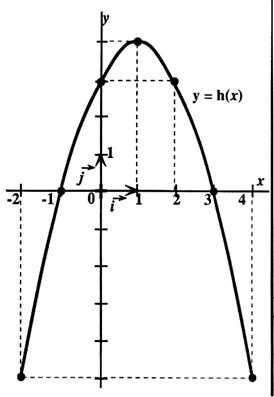
Voici la représentation graphique d’une fonction
« h » définie sur l’intervalle [ - 2 ; 4 ] Utiliser le graphique pour répondre aux questions
suivantes : On notera que le point « · »
sont sur la courbe et ont pour
coordonnées des nombres entiers. 1°) Dresser
le tableau de variation de « h » 2°) Donner les solutions de l’équation : h
(x) = 0 3°) Etudier le signe de h(x) sur l’intervalle [ -
2 ; 1] 4°) Donner
l’ensemble des solutions de l’inéquation : h(x) ³ 3 |
|
|
|
|
|
|
|
|
ACTIVITES COMPLEMENTAIRES :
|
LES FONCTIONS : |
|||||||
|
I ) Génération et description des fonctions |
Liste
des tests |
||||||
|
|
a) Exemples de modes de génération de fonctions. |
|
|
|
|
|
|
|
|
Exemples de description d’une situation à l’aide
d’une fonction. |
|
|
|
|
|
|
|
|
Représentation graphique d’une fonction dans un
repère ortho normal ou orthogonal. |
|
|
|
|
|
|
|
|
b) Exemples simples de calculs de valeurs d’une
fonction à l’aide d’une calculatrice. |
|
|
|
|
|
|
|
|
c) Parité , périodicité. : maximum , minimum
d’une fonction, fonctions croissantes, fonction décroissantes |
|
|
|
|
||
|
|
d) exemples de lecture de propriétés de fonctions
à partir de leur représentation graphique. |
|
|
|
|
||
|
II ) Fonctions usuelles. |
Liste
des tests |
||||||
|
|
a) Variations et représentation graphiques des
fonction : x ® a x + b ; x ®
x² ; x ® x 3 ;
x ® |
|
|||||
|
|
b) Exemples simples d’études de comportements de
fonctions tels que : signe , variations, recherche de maximum et de
minimums, représentations graphiques dans un repère (orthonormal ou
orthogonal). |
|
|
|
|||
|
|
c) Exemples simples d’étude graphique d’équation
de la forme f (x) = l où l a une valeur numérique donnée. |
|
|
|
|||
|
|
d)Etude des fonctions cosinus et sinus : périodicité , symétries, sens de variation.
Courbes représentatives. |
|
|
|
|||
|
|
|
|
|
|
|
|
|