PRE REQUIS DOSSIER : LES FONCTIONS
RESUME sur l’ étude de la
représentation graphique d’une FONCTION NUMERIQUE.( généralités )
|
|
·
Rappels sur le tracé d’une fonction ou non fonction. |
. |
|
|
·
Etude du tracé d’une fonction. |
. |
|
|
·
Sens de variation (tableau de variation) |
. |
|
|
·
Maximum, minimum. |
. |
|
|
·
Parité. |
. |
|
|
·
Résumé : ce qu’il faut savoir faire lorsque l’on demande d’étudier
el graphique d’une fonction…. |
|
Intérêt : savoir étudier un tracé
dans des matières interdisciplinaires (physique, chimie , géographie, histoire, statistique,….)
INFO : MOTS CLEFS : l’ensemble de définition ;taux d’accroissement, tableau
de variation , représentation graphique ; utiliser le repère cartésien . le
plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » )
On retiendra :
Lorsque l’on vous demande
d’ étudier la représentation graphique d’une fonction
on doit :
-1°) Savoir
Identifier, par la forme du tracé, le type de l’équation qui à permis de réaliser ce tracé..(l’allure de la
courbe) : linéaire, affine , du second degré, du troisième degré , racine
, inverse (homographique), sinusoïde
représentant un sinus ou un cosinus ;…..Il savoir dire si la
fonction est périodique ou non périodique.
- 2°) Identifier
ce qui caractérise le tracé d’« une
fonction ».
· -Savoir donner
le domaine de définition. (pour quelles valeurs de « x »
le tracé sera le représentant de la
fonction)
-
Savoir identifier les
bornes des intervalles de « x ». ou savoir donner les valeurs mini et maxi de
« x » qui limite l’étude du tracé .
-
Savoir identifier dans
un intervalle donné, l’allure de la
courbe. Dire si la fonction est croissant, décroissante,
constante.
-
Dans un tracé continu d’une fonction pouvant être successivement :
« croissant », « décroissant », « constant », il
faut savoir identifier le point de passage de changement de
« pente » : Est-il « maximum » ou
« minimum ». et éventuellement
quelles sont les coordonnées de ce point ?
- 3°) Pour rendre
compte de l’étude d’une fonction (observation sur le tracé) il faut savoir construire
et compléter et remplir un tableau de variation.
Pour « x » :
-
on indiquera : «les
valeurs des bornes de chaque intervalle»,
-
la valeur de « x » qui indique un changement de
pente.
-
Si la courbe coupe l’axe
des « x » on donnera l’ abscisse ou les
abscisses de ces points.
Pour f(x) :
-
pour les valeurs particulières de « x » on calculera
les valeurs « f(x) » correspondantes. De ces valeurs partira et
arrivera la flèche
4°) On complétera l’étude en indiquant
- si la fonction
est « paire » ou « impaire ».
-
si elle est périodique (ou non périodique)
|
|
Exemple d’application : |
|
|
|
|
|
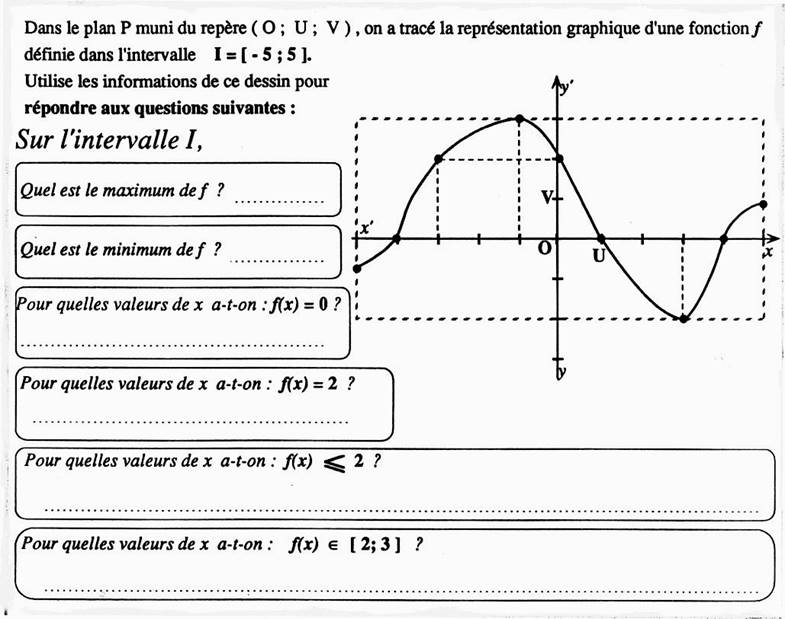
Maximum
de f = 3 Minimum
de f = - 3 f(x) = : - 4 ; 1 ; 4 f(x) = 2 ; 0 et - 3 f (x) £
2 : x Î [ - 5 ; - 3 ] È [ 0 ; 5 ) ] f (x) Î [ 2 ; 3 ] ;
réponse : x Î [ -
3 ; 0 ] |