|
DOC : formation
individualisée soutien en ligne. |
DOC : livre Elève .Cours interactifs - et travaux + corrigés. |
|
DOSSIER N°23 INTERACTIF |
Information « TRAVAUX » |
|
OBJECTIFS : savoir présenter l’étude d’une fonction linéaires |
||
|
|
|
|
|
Etudes Niveau V
(dossier 23) |
|
Pré requis:
|
|
ENVIRONNEMENT du
dossier:
|
Index |
Objectif précédent : |
Objectif suivant : |
DOSSIER : ETUDES DES FONCTIONS LINEAIRES
1°)
Rappel : ETUDE « TYPE » D’ UNE
FONCTION .
Ensuite : études d’exemples
2°) exemple
d’étude : x
-3x
|
|
|
|
|
|
|||
|
TEST |
COURS |
Devoir
Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle
|
Corrigé évaluation
|
COURS
1°) ETUDE « TYPE » D’
UNE FONCTION :
Etudier
une fonction c’est :
A
partir de 
x 
f(x)
1°)donner l’ensemble de définition.
2°)faire une étude aux bornes du domaine de définition :
a) que
se passe-t-il pour f (x) quand « x » tend vers -¥ ?
b) que
se passe-t-il pour f (x) quand « x » tend vers +¥ ?c) que se passe-t-il pour f (x)
quand « x » = 0
d)
résoudre f (x) = o
3°)donner le sens de
variation : calculer
le taux d’accroissement
4°)
construire le tableau de variation :
type
|
x |
-¥
0 +¥ |
|
|
? ? ? ? ?sens donner avec des flèches |
5°)
faire la représentation graphique : utiliser le repère cartésien . le
plus utilisé est le repère cartésien orthonormé ( dit
aussi « orthonormal » )
|
Repère
cartésien |
|
|
FONCTION
LINEAIRE : f : |
|
|
Etudes d’exemples
|
|
|
|
|
|
|
|
Exemple 1 f
: R
1°)Ensemble de définition. Df = R 2°) Etude aux bornes du domaine de définition Df: a)
que
se passe-t-il pour f (x) quand « x » tend vers -¥ ? f (x) tend vers +¥ quand « x » tend
vers -¥ b)
que se passe-t-il pour f (x) quand « x » tend vers +¥ ? f (x) tend vers -¥ quand « x » tend
vers +¥ c)
que se passe-t-il pour f (x) quand « x » = 0
d)
résoudre f (x) = o 0 = -3
x donc x = 0 3°) Sens de variation :
Il faut calculer le taux d’accroissement ? : pas nécessaire le taux
correspond à « a » le
coefficient de « 4°) le tableau de
variation : |
|
|
x |
-¥ 0 +¥ |
|
|
+¥ 0 -¥ |
|
|
5°) Représentation graphique : |
|
|
|
|
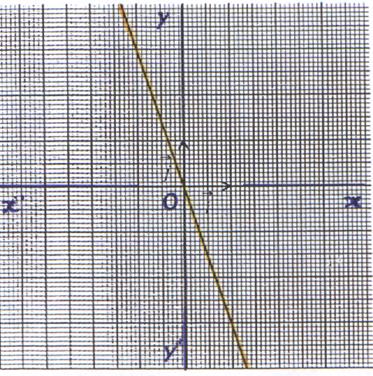
La représentation graphique de la fonction f est une droite d’équation
passant par l’origine du repère et le point de coordonnées (1 ; -3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FONCTION LINEAIRE : f : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemple
2
f : R 
R
1°) Ensemble de définition. Df = R
2°)Etude aux bornes du domaine de
définition Df:
b)
que se
passe-t-il pour f (x) quand « x » tend vers -¥ ?
f (x) tend vers +¥ quand « x » tend vers +¥
b) que
se passe-t-il pour f (x) quand « x » tend vers +¥ ?
f (x) tend vers -¥ quand « x » tend vers -¥
c) que
se passe-t-il pour f (x) quand « x » = 0
f (o) = o
d)
résoudre f (x) = o 0 = 2 x donc x = 0
3°)Sens de
variation :
calculer le
taux d’accroissement : pas nécessaire le taux correspond à « a »
le coefficient de
« x » est négatif ( a = 2 ) , f est donc strictement croissante sur Df
4°) le tableau de
variation :
|
x |
-¥ 0 +¥ |
|
|
+¥ 0 -¥ |
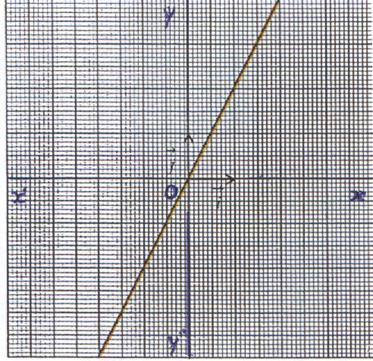
5°) Représentation graphique :
|
La représentation graphique de la fonction f est une droite d’équation
|
|
Cas général :
|
f : |
INFORMATIONS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f : R R
1°)Ensemble de définition. Df = R
2°)Etude aux bornes du domaine de
définition Df:
|
a
< 0 |
a
> 0 |
|
f
(x) tend vers +¥ quand
« x » tend vers -¥ f
(x) tend vers -¥ quand
« x » tend vers +¥ f
(o) = o |
f
(x) tend vers +¥ quand
« x » tend vers +¥ f (x) tend vers -¥ quand « x » tend vers -¥ f
(o) = o |
3°)Sens de
variation :
|
a
< 0 |
a
> 0 |
|
f est
donc strictement décroissante sur Df |
f est
donc strictement croissante sur Df |
4°) le tableau de
variation :
|
a
< 0 |
|
a
> 0 |
||
|
x |
-¥
0 +¥ |
|
x |
-¥
0 +¥ |
|
|
+¥ 0 -¥ |
|
f(x) |
+¥ 0 -¥ |
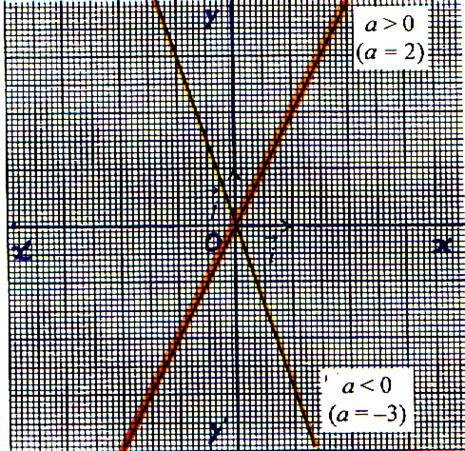
5°) Représentation graphique :
|
D1
y = a x passant par l’origine du repère (0 ;0 ) et le point de coordonnées (1 ; a ). Deux cas : les droites sont croissantes ou décroissantes passant
par le point « O » La droite D1 est
dite « décroissante » La droite D2 est dite « croissante » |
|
||
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
1°) Donner les étapes d’étude d’une fonction : SOLUTION : Etudier une fonction c’est : A partir de
1°) Donner l’ensemble de définition. 2°)faire une étude aux bornes du domaine
de définition : a) que se passe-t-il pour f
(x) quand « x » tend vers -¥ ? b) que se passe-t-il pour f
(x) quand « x » tend vers +¥ ? c) que se passe-t-il pour f
(x) quand « x » = 0 d) résoudre f (x) = o
3°) Donner le sens de
variation : calculer le taux d’accroissement 4°) construire le tableau de variation : |
|
|
|
|
|
type
|
x |
-¥
0
+¥ |
|
|
? ? ? ? ?sens donner avec des flèches |
|
|
5°) Faire la représentation
graphique : utiliser le repère cartésien . le plus utilisé est le repère cartésien orthonormé ( dit aussi « orthonormal » ) |
|
|
|
|
|
|
|
|
|
|
|
|
|